数据结构（2）树状数组

活动 - AcWing

参考：《算法竞赛进阶指南》-lyd

目录

一、概念

1.主要功能

2.实现方式

3.

二、例题

1.树状数组和逆序对

2.树状数组和差分

3. 两层差分

4. 结合二分

---

 

一、概念

1.主要功能

树状数组可以完成的功能主要有：

• 维护序列的前缀和
• 单点修改

上述两个操作在树状数组中都是logn级别的。对比前缀和数组和原始序列

前缀和数组查询前缀和o（1），但是单点修改o（n）。原始数组求前缀和o（n），单点修改o（1）。所以在大量的查询和修改操作并存的情况下，树状数组表现更优秀。

2.实现方式

注意下标从1开始

对一个较大的连续线性范围进行统计时，我们把它按照2的整数次幂分成若干个小范围进行预处理和计算。若一个正整数x的二进制表示为，设其中等于1的位分别是则正整数x可以被“二进制分解成”：

设i1>i2>...>im，则区间[1,x]可被划分为logx个小区间：

1. 长度为2^i1的区间[1,2^i1]
2. [2^i1 + 1,2^i1 + 2^i2]
3. [2^i1 + 2^i2 + 1,2^i1 + 2^i2 + 2^i3]
4. ......
5. [2^i1 + 2^i2 + 2^i3+...+ 2^im-1 + 1,2^i1 + 2^i2 + 2^i3+...+ 2^im]

他们的特点是：若区间结尾为R，则区间长度等于lowbit（R）

树状数组就是基于上述思想的数据结构。对于原始序列a，我们建立树状数组tr，存储划分后每个区间的和。即：

那么求前缀和可转化为

for(int i=x;i<=n;i+=lowbit(i)) res+=tr[x]
return res

有logn个区间，所以复杂度logn。

接下来考虑怎么构建这样的树状数组：

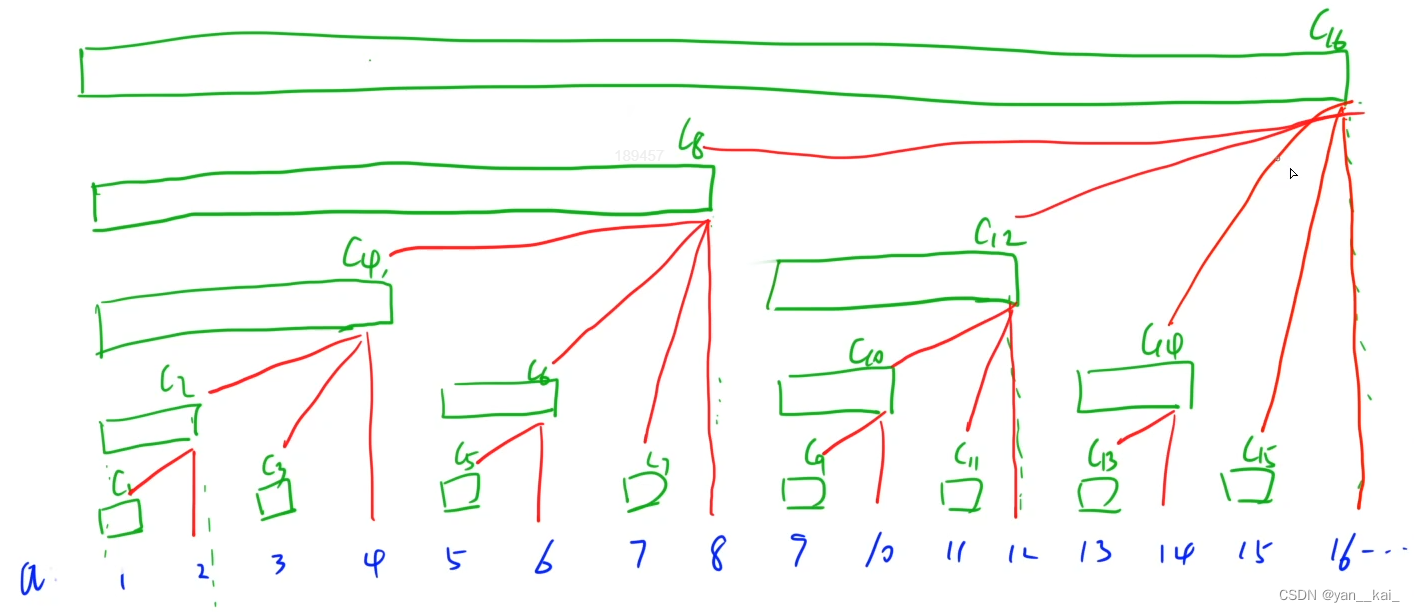
画一下经典1-16的区间图。很容易发现之中的树状关系。接下来我们找一下子节点和父节点的下标的关系。

对于一个子节点，父节点编号y和子节点编号x有关系：

对父节点，子节点编号为

for(;x;x-=lowbit(x)) 

3.

对于查询操作：遍历所有子节点u1=x，u2=u1-lowbit(u1),.....un=1

对于修改操作，设单点x增加d

则把所有相关的父节点更新。父节点编号u1=x,u2=u1+lowbit(u1)......un=N

二、例题

1.树状数组和逆序对

 dp思想：将所有V和A按中间顶点位置划分。

对于顶点i，其V数量为在它左边比他大的数的个数  乘以  在它右边比他大的数的个数

A数量反之。

因此我们需要处理：在遍历到第i个点前，比y（i）大的数的个数和比y（i）小的数的个数

对此，我们应该记录，在遍历到i点前，每个y（x）出现的次数

这样，比yi大的数的个数为sum（n）-sum（y），比yi小的数的个数为sum（y）

处理完之后add（yi，1）即可

因此需要维护一个查询前缀和，支持单点修改的数组，并且复杂度不能n方，树状数组符合要求。

V A 数量 正反遍历一遍即可

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N =2e5+10;

typedef long long LL;

int n;
int a[N];
int tr[N];//树状数组的原数组是 数字i出现的次数。
int Greater[N];
int Lower[N];


int lowbit(int x)
{
    return x&(-x);
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}

int sum(int x)
{
    int res=0;
    for(int i=x;i;i-=lowbit(i))
    {
        res+=tr[i];
    }
    return res;
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];

    for(int i=1;i<=n;i++)
    {
        int y=a[i];
        Lower[i]=sum(y-1);
        Greater[i]=sum(n)-sum(y);
        add(y,1);
    }
    memset(tr,0,sizeof tr);
    LL resV=0,resA=0;
    for(int i=n;i;i--)
    {
        int y=a[i];
        resV+=(LL)Greater[i]*(sum(n)-sum(y));
        resA+=(LL)Lower[i]*(sum(y-1));
        add(y,1);
    }
    cout<<resV<<" "<<resA<<endl;
    return 0;
}


作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5174438/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

2.树状数组和差分

 题目要求：区间增加，单点查询。

用树状数组维护原数组的差分数组，即可把条件转化为单点增加，区间查询。符合要求

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;

typedef long long LL;
const int N =1e5+10;

int n,m;
int a[N];
int tr[N];

int lowbit(int x)
{
    return x&(-x);
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}

LL sum(int x)
{
    LL res=0;
    for(;x;x-=lowbit(x)) res+=tr[x];
    return res;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        add(i,a[i]-a[i-1]);
    }
    while(m--)
    {
        char op[2];
        int l,r,d;
        scanf("%s%d",op,&l);
        if(*op=='C')
        {
            scanf("%d%d",&r,&d);
            add(l,d),add(r+1,-d);
        }
        else
        {
            cout<<sum(l)<<endl;
        }
    }
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5174626/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

3. 两层差分

 题目要求：区间增加，区间查询。

 推导一下：可知a1=b1，a2=b1+b2。。。。写成三角矩阵，补齐右上角

可推导出：

 

因此维护一个a的差分数组b，再维护一个i*ai的差分数组即可。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
#include<cstdio>

typedef long long LL;
const int N =1e5+10;


int n,m;
LL tr1[N];
LL tr2[N];
int a[N];

int lowbit(int x)
{
    return x&-x;
}

void add(LL tr[],int x,LL c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}

LL sum(LL tr[],int x)
{
    LL res=0;
    for(;x;x-=lowbit(x)) res+=tr[x];
    return res;
}

LL presum(int x)
{
    return (x+1)*sum(tr1,x)-sum(tr2,x);
}


int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        int b=a[i]-a[i-1];
        add(tr1,i,b);
        add(tr2,i,(LL)b*i);
    }

    while(m--)
    {
        char op[2];
        int l,r,d;
        scanf("%s%d%d",op,&l,&r);
        if(*op=='C')
        {
            scanf("%d",&d);
            add(tr1,l,d),add(tr1,r+1,-d);
            add(tr2,l,l*d),add(tr2,r+1,-(r+1)*d);
        }
        else
        {
            cout<<presum(r)-presum(l-1)<<endl;
        }
    }
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5174858/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

4. 结合二分

只知道前面有几头比第i头低。

因此我们从后往前推导，由于身高各不相同，设：备选序列1~n，

我们直接可以知道第n头就是第ai+1高的，即ai+1，则往前推，第n-1头就是备选序列去掉ai+1之后，剩下第a（n-1）+1高的。

因此我们需要的操作是：快速找出序列中第k高的，转换一下，备选序列可选即1，已被选为0，则操作变为快速找出一个x，使得sum（x）==k。因此树状数组可做，找出这个x可用二分查找

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
using namespace std;

const int N=1e5+10;
int n;
int a[N];
int tr[N];

int lowbit(int x)
{
    return x&-x;
}

void add(int x,int c)
{
    for(int i=x;i<=n;i+=lowbit(i)) tr[i]+=c;
}
int sum(int x)
{
    int res=0;
    for(;x;x-=lowbit(x)) res+=tr[x];
    return res;
}


bool check(int mid,int k)
{
    return sum(mid)>=k;
}


int main()
{
    cin>>n;
    for(int i=2;i<=n;i++)
    {
        cin>>a[i];
    }

    for(int i=1;i<=n;i++)
        add(i,1);


    for(int i=n;i>=1;i--)
    {
        int k=a[i];
        k++;
        int l=1,r=n;
        while(l<r)
        {
            int mid=l+r>>1;
            if(check(mid,k))  r=mid;
            else l=mid+1;
        }
        a[i]=l;
        add(l,-1);
    }
    for(int i=1;i<=n;i++) cout<<a[i]<<endl;
    return 0;

}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/5175077/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。