第十三课：容斥原理、简单博弈论

目录

一、容斥原理

 例题

 二、简单博弈论（Nim）

 （1）Nim游戏

习题：台阶Nim游戏（考虑构成胜败态的因素）

（2）集合—Nim游戏

 mex运算

sg函数

 必胜/败状态

习题：拆分—Nim游戏

---

---

一、容斥原理

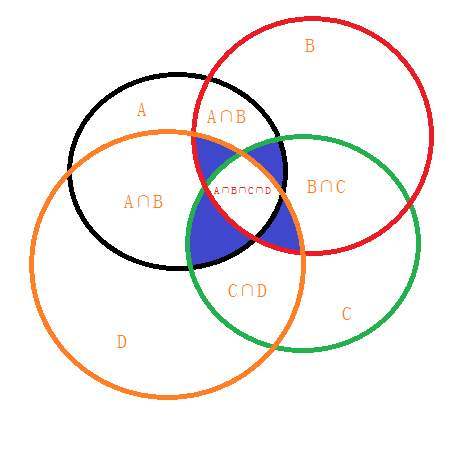
 容斥原理高中基本有涉猎，本身不再细讲，直接给出上图中四圆覆盖面积：

 例题

分析：1.运用容斥原理计算。2.为了使用容斥原理，需要搞清楚如何遍历所有项。

容斥原理结果中，项数为：

 其中，组合数上标为奇数时，该项为正，为偶数时则为负。因此我们可以用一个m位二进制数表示。第i位表示该项包不包括第i个质数。例：0101表示。

由求解高精度组合数中我们学到，1~n中p的倍数的个数为：。至此，由上述知识基础该题易解，代码如下：

//这里填你的代码^^
#include<iostream>
using namespace std;

typedef long long LL;
const int N =20;
int n,m;
int p[N];


int main()
{
    cin>>n>>m;
    for(int i=0;i<m;i++)
        cin>>p[i];

    int res=0;
    for(int i=1;i< 1<<m;i++)//遍历所有情况，，2的m次方
    {
        int cnt=0,t=1;
        for(int j=0;j<m;j++)
        {
            if(i>>j&1)
            {
                if((LL)t*p[j]>n)//必不可能整除n
                {
                    t=-1;
                    break;
                }

                t*=p[j];
                cnt++;
            }
        }
        if(t!=-1)
        {
            if(cnt%2) res+=n/t; //如果计算了奇数个集合
            else res-=n/t;
        }
    }
    cout<<res;
    return 0;

}
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/3782804/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

 二、简单博弈论（Nim）

先解释两个名词：

1.必胜态：总有办法走一步，使得局面变为必败态。

2.必败态：无论怎么走，都会使得局面变为必胜态。

 （1）Nim游戏

 针对此类游戏，我们设每堆石子中石子数为a（i），终局时石子数全为0，为必败态。

首先给出结论，必败态为：

必胜态为：

证明：

  先将每个石子数写成二进制形式。首先证明，必胜态一定可以只走一步，使得局面变为必败态。

必胜态时：

设x二进制表示中最高一位为第k位。则a1~an中必然有ai，其第k位是1。由于，于是我们在第i堆拿走个石子，使得拿走后，原式变为：

                                

                                

                                

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

得证。

再证明，必败态无论怎么走，都会变成必胜态。 

必败态时：

设在第i堆拿走一些石子，使得，运用反证法，若走完该步之后，仍为必败态，即：

两式子异或：

矛盾！因此必败态无论怎么走，必定变成必胜态。

        本次游戏中，由于每次必须拿走一些石子，所以游戏最终会结束，归于必败态（终局）。所以只需要一开始时，石子堆是必胜态，先手就必胜，后手永远处于必败态，直到游戏结束。若一开始石子是必败态，则先手必败。

#include<iostream>
using namespace std;

int main()
{
    int n;
    cin>>n;
    int res=0;
    while(n--)
    {
        int x;
        cin>>x;
        res^=x;
    }
    if(res) puts("Yes");
    else puts("No");
    return 0;
    
}

习题：台阶Nim游戏（考虑构成胜败态的因素）

 思考方式同经典Nim游戏，不过本题只需要考虑奇数阶上的台阶的石子数量异或和。

原因：1.如果后手移动奇数台阶，其情形等同经典Nim游戏，我们可以知道先手必然可以通过某种方式把异或和变成0.

           2.如果后手移动偶数台阶，先手只需要把后手移动的再移下去，局面等同于没有变化。

为什么是奇数台阶而不是偶数台阶：偶数台阶异或为0不是必败态，因为移动一号台阶不改变异或值，不符合必败态定义。

#include<iostream>
/*①当后手移动偶数台阶上的石子时，先手只需将对手移动的石子继续移到下一个台阶
这样奇数台阶的石子相当于没变，于是留给后手的又是奇数台阶异或为0的状态

②当后手移动奇数台阶上的石子时，留给先手的奇数台阶异或非0
根据经典Nim游戏，先手总能找出一种方案使奇数台阶异或为0*/


/*为什么不是偶数台阶？  偶数台阶异或为0不是必败态，因为移动一号台阶不改变异或值，不符合必败态定义*/
using namespace std;

const int N =100010;
int a[N];
int n;

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    int res=0;
    int i=1;
    while(i<=n)
    {
        res^=a[i];
        i+=2;
    }
    
    if(res) puts("Yes");
    else puts("No");
    return 0;
    
    
}

（2）集合—Nim游戏

 mex运算

        设一集合S，mex（S）即该集合所不能到达的最小自然数。

sg函数

        在有向图游戏中，对于每个节点x，设从x出发有k条边，分别到达后继节点y1，y2...yk。则我们定义SG（x）为以x的所有后继节点的函数值所构成的集合，执行一次mex运算的结果。

​​​​​​​

 必胜/败状态

同上，必胜态（Gi为起点，默认出度为0的点为结束点，SG为0）：

必败态：

首先，我们仅以一个有向图游戏为例：

则我们需要证明：1.若当前节点SG为0，则为必败态。2.若当前节点SG为1，则为必胜态。

 进一步来说，需要证明：1.SG为0的点只能走到SG不为0的节点。2.SG不为0的节点总能走到SG为0的节点。3.游戏总会结束，且终点的SG为0。

事实上，由于mex运算的特点，上述三点是显然成立的。

对于多个有向图游戏，证明方法同上：终局时，所有SG异或和为0；若不为0，总能使得其变为0；若为0，无论怎么走都走不回为0的状态。因此得证。

习题：拆分—Nim游戏

 分析：1.游戏必然会结束，结束时所有堆石子变成0。（题意解释：取走石子数为x的一堆石子，在增加两堆石子数都小于x的石子堆。这样单个石子堆的数量只能越来越小，最终变为0）。

2.一个局面的sg函数，是其拆1分局面sg函数的异或和（等同于多个有向图游戏）。

3.其余同集合Nim游戏，sg异或和为0则为必败态，反之为必胜态。

//这里填你的代码^^
#include<iostream>
#include<algorithm>
#include<unordered_set>
#include<cstring>
using namespace std;
const int N =110;
int f[N];
int sg(int x)
{
    if(f[x]!=-1) return f[x];
    unordered_set<int> S;
    for(int i=0;i<x;i++)
        for(int j=0;j<=i;j++)
            S.insert(sg(i)^sg(j));//合并子堆 的 游戏的局面

    for(int i=0;;i++)
        if(!S.count(i))
            return f[x]=i;

}


int main()
{
    memset(f,-1,sizeof f);
    int res=0;
    int n;
    cin>>n;
    while(n--) 
    {
        int x;
        cin>>x;
        res^=sg(x);
    }
    if(res) puts("Yes");
    else puts("No");
    return 0;
}
//注意代码要放在两组三个点之间，才可以正确显示代码高亮哦~

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/3798278/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。