动态规划（5）状态压缩dp

最新推荐文章于 2024-05-01 05:00:00 发布

BlessingSoftware1

最新推荐文章于 2024-05-01 05:00:00 发布

阅读量483

点赞数 1

分类专栏：摆烂日记from acwing 文章标签：动态规划算法

本文链接：https://blog.csdn.net/weixin_64197656/article/details/126757428

版权

摆烂日记from acwing 专栏收录该内容

45 篇文章 1 订阅

订阅专栏

一、概述

动态规划的过程是随着阶段不断增长，在每个状态维度上不断扩展。在任意时刻，已经求出最优解的状态与尚未求出最优解的状态在各维度上的分界点组成了dp扩展的轮廓，对于某些问题，我们需要在动态规划的状态中记录一个集合，保存这个轮廓的详细信息，以便状态转移。

若集合中每个元素都是小于K的自然数，集合大小不超过N，则我们可以用一个N位的K进制数作为dp状态一维。这种把集合转化为整数记录在dp状态中的算法被称为状态压缩dp

（摘自“算法竞赛进阶指南”）

二、例题

（1）棋盘类

此类型题一般的状态表示为：摆放好前i行，摆放了多少个（看题目要求），前几行的状态是xx（看题目要求，需要几行状态就开几维）。

需要注意的有：预处理，如何判断状态是否合法。

（1）小国王

我们用长度为n的二进制数表示某一行上摆放国王的状态，0表示不摆放，1表示摆放。

国王只能攻击相邻的八个格子。因此需要满足如下条件：

某一个位和它下一位不能同时为1。
状态转移时，设有两行a，b。则a，b同一位不能同时为1，
a|b之后，某一位和它下一位不能同时为1

类比蒙德里安的梦想。本题状态表示f[n,k,m]摆放好前n行棋盘，摆放了k个国王，第n行状态是m的方案数。

此类型题一般预处理出某个合法状态，和它所有能到的状态。

因此状态转移方程为（设第i行状态是a，第i-1行是a所有能到的状态中的一种b）

$f[i,j,a]+=f[i-1,j-cnt[a],b]\ \ \ (j-cnt[a]>0)$

那么最后答案应该是摆放好了前n行，摆放了k个，第n行状态是xxx。但是我们并不知道最后摆放完第n行状态是什么。但是我们发现，第n+1行一定不摆放，且前n+1行同样摆放了k个国王。

因此答案可以转化为：摆放好了前n+1行，摆放了k个，第n+1行状态是0。即f[n+1][k][0]；在dp的过程中做到n+1行即可。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;
const int N =12,M=1<<10,K=110;

long long  f[N][K][M];
vector<int> state;
int cnt[M];
vector<int> head[M];
int n,m;

bool check(int state)
{
    for(int i=0;i<n;i++)
        if((state>>i&1)&&(state>>i+1&1))
            return false;
    return true;
}

int count(int state)
{
    int res=0;
    for(int i=0;i<n;i++) res+=state>>i&1;
    return res;
}

int main()
{
    cin>>n>>m;
    for(int i=0;i<1<<n;i++)
        if(check(i))
        {
            state.push_back(i);
            cnt[i]=count(i);
        }
    for(int i=0;i<state.size();i++)
        for(int j=0;j<state.size();j++)
        {
            int a=state[i],b=state[j];
            if((a&b)==0&&check(a|b))
                head[i].push_back(j);
        }
    f[0][0][0]=1;
    for(int i=1;i<=n+1;i++)
        for(int j=0;j<=m;j++)
            for(int a=0;a<state.size();a++)
                for(int b:head[a])
                {
                    int c=cnt[state[a]];
                    if(j>=c)
                        f[i][j][a]+=f[i-1][j-c][b];
                }


    cout<<f[n+1][m][0]<<endl;
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4147228/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（2）玉米田

与上题类似，状态表示为摆放前i行，第i行状态是j的所有方案。

预处理：

不能出现连续两个1
每行预处理一个数，如果该列土地肥沃则该位置为0，土地不育则置为1（这样做和该行状态做“与”运算，若结果不为0则可判断为非法）
上一行和下一行做与运算结果为0。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

const int N =14,M=1<<N;
const int mod=1e8;

int f[N][M];
int n,m;
vector<int> state;
vector<int> head[M];
int g[N];

bool check(int state)
{
    for(int i=0;i<m;i++)
        if((state>>i&1)&&(state>>i+1&1)) return false;
    return true;
}

int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=0;j<m;j++)
        {
            int t;
            cin>>t;
            g[i]+=!t<<j;
        }    

    for(int i =0;i<1<<m;i++)
        if(check(i))    
            state.push_back(i);

    for(int i=0;i<state.size();i++)
        for(int j=0;j<state.size();j++)
        {
            int a=state[i],b=state[j];
            if((a&b)==0)    head[i].push_back(j);
        }


    f[0][0]=1;
    for(int i=1;i<=n+1;i++)
        for(int a=0;a<state.size();a++)
            for(int b:head[a])
            {
                if(g[i]&state[a]) continue;
                f[i][a]=(f[i][a]+f[i-1][b])%mod;
            }
    cout<<f[n+1][0]<<endl;
    return 0;
}


作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4147518/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（3）炮兵阵地

炮兵的攻击范围是两个格子，意味着某一行填的状态和该行前两行都有关系，因此我们的状态表示为：填好了前i行，第i行的状态是b，第i-1行的状态是a，方案中，最多摆放炮兵部队的数量。方案划分的依据是第i-2行的状态。

根据题目，我们提取出限定状态转移的规则：

有的地方是山地，不能摆放炮兵，因此像上一题“玉米地”那样，每行处理出一个二进制数g，如果该位不可以摆放炮兵则置为1，则第i行状态b|g==0时，状态合法
受炮兵攻击距离为两个的影响，在同一行上，不能有两个炮兵的距离小于等于2，同一列上如此。用代码表达为：判断(state>>i&1)&&((state>>i+1&1)|(state>>i+2&1))==0，以及判断(a&b)|(b&c)|(a&c)==0。

其他细节：同上一题一样，我们不知道最佳方案填完n行时，第n行以及第n-1，n-2行的状态。因此我们填n+2行，答案就存储在f[n+2][0][0]中。由于行数可能过大，我们也只需要用到两层的数据，因此可以运用滚动数组来做。

#include<iostream>
#include<algorithm>
#include<cstring>
#include<vector>
using namespace std;

const int N =110,M=1<<11;

int n,m;
int f[2][M][M];//第i行是b，第i-1行是a，以第i-2行c的情况做状态划分
vector<int> state;
int cnt[M];
int g[N];

int count(int state)
{
    int res=0;
    for(int i=0;i<m;i++)  res+=state>>i&1;
    return res;
}

bool check(int state)
{
    for(int i=0;i<m;i++)
        if((state>>i&1)&&((state>>i+1&1)|(state>>i+2&1))) return false;
    return true;
}


int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++)
        for(int j=0;j<m;j++)
        {
            char c;
            cin>>c;
            if(c=='H') g[i]+=1<<j;
        }

    for(int i=0;i<1<<m;i++)
        if(check(i)) 
            state.push_back(i),cnt[i]=count(i);


    for(int i=1;i<=n+2;i++)
        for(int j=0;j<state.size();j++)
            for(int k=0;k<state.size();k++)
                for(int u=0;u<state.size();u++)
                {
                    int a=state[j],b=state[k],c=state[u];
                    if((a&b)|(b&c)|(a&c)) continue;
                    if(g[i-1]&a|g[i]&b) continue;
                    f[i&1][j][k]=max(f[i&1][j][k],f[i-1&1][u][j]+cnt[b]);
                }

    cout<<f[n+2&1][0][0];
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4149830/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（2）集合类

用一个二进制数表示已经遍历过的集合或者还未遍历过的集合。

（1）愤怒的小鸟

首先处理出任取两个点i，j构成抛物线，该抛物线经过的所有点。

本题直觉上应该采用搜索思路，搜索所有可能的覆盖全部点的方案，更新全局最小值ans。

但是用记忆化搜索的方式明显更容易完成。用f[state]存储到达这个状态的最小步数。同样的，任选还没有被覆盖的一列，枚举所有能覆盖x的抛物线path[x][j]。状态转移方程为：

$f[i|path[x][j]]=min(f[i|path[x][j]],f[i]+1);$

接下来借本题说明预处理path数组的细节。

由于浮点数表示有误差，所以判断两个数是否相等是看两个数差的绝对值是否是一个很小的数。
path[i][i]=1<<i; //特判只有一个点
如果i，j两个点的x相等，则抛物线不存在。
有本题的特点，抛物线二次项系数小于0。所以求得a大于0的抛物线舍去
由0，i，j两点计算的抛物线公式为a=(y1/x1-y2/x2)/(x1-x2)，b=y1/x1-a*x1：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#define x first
#define y second
using namespace std;
//path所有能覆盖x的抛物线
typedef pair<double,double> PDD;

const double eps=1e-8;
const int N =18,M=1<<18;

int n,m;
PDD q[N];
int f[M];//记忆化搜索
int path[N][N];

int cmp(double x,double y)
{
    if(fabs(x-y)<eps) return 0;
    if(x<y) return -1;
    return 1;
}


int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        cin>>n>>m;
        for(int i=0;i<n;i++) cin>>q[i].x>>q[i].y;

        memset(path,0,sizeof path);//以i，j两个点构成的抛物线所覆盖的点
        for(int i=0;i<n;i++)
        {
            path[i][i]=1<<i;//特判只有一个点

            for(int j=0;j<n;j++)
            {
                double x1=q[i].x,y1=q[i].y;
                double x2=q[j].x,y2=q[j].y;
                if(!cmp(x1,x2)) continue;//在同一列，抛物线不存在
                double a=(y1/x1-y2/x2)/(x1-x2);
                double b=y1/x1-a*x1;

                if(cmp(a,0)>=0) continue;//抛物线不合要求
                int state=0;
                for(int k=0;k<n;k++)
                {
                    double x=q[k].x,y=q[k].y;
                    if(!cmp(a*x*x+b*x,y)) state+=1<<k;
                }
                path[i][j]=state;
            }

        }

        memset(f,0x3f,sizeof f);
        f[0]=0;
        for(int i=0;i+1<1<<n;i++)
        {
            int x=0;
            for(int j=0;j<n;j++)//找出一个未覆盖的点
                if(!(i>>j&1))
                {
                    x=j;
                    break;
                }

            for(int j=0;j<n;j++)
                f[i|path[x][j]]=min(f[i|path[x][j]],f[i]+1);
        }
        cout<<f[(1<<n)-1]<<endl;

    }
    return 0;
}


作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4154995/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

（2）宝藏

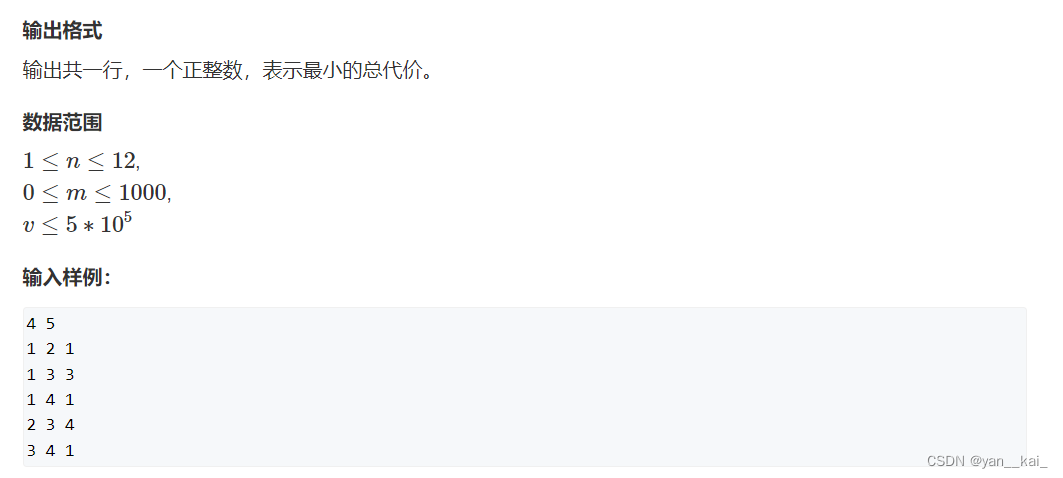
根据题意，已经开凿出的道路可以任意同行而不消耗代价，因此最后修建的道路一定构成一颗树。若不然，则一定存在一条多余的道路，删去之后宝藏屋仍然连通。赞助商帮忙打通的宝藏屋就是这个树的根。

因此本题容易想到搜索算法：

任选一个点为根
任选一个已经打通的宝藏屋x，从它出发开辟一条道路，到达一个未打通的宝藏屋y，代价为道路x->y的距离乘节点x的深度，然后继续搜索。

如果每次递归过程，都dfs一遍所有已经打通的宝藏屋，试图开辟一条道路，那么该算法遍历了相当多的重复状态，时间复杂度非常高。因此可以做两点限制：

从浅到深打通宝藏屋
对于已打通宝藏屋集合S，对于相同的集合S，我们只关心代价最小的一个。

第一点形成了从浅到深的动态规划的“阶段”，第二点是动态规划“最优子结构”的性质。

因此根据这两点可以写出状态表示f[i,j]，表示已经打通的宝藏屋最大深度为i，宝藏屋的打通状态n位二进制数j。集合划分为树的深度。

状态转移：求出第i层的所有点到j的最短边，将这些边权和乘以深度i，直接加到f[i-1][S]上，即可求出f[i][j]。

证明：
将这样求出的结果记为f'[i][j]

f[i][j]中花费最小的生成树一定可以被枚举到，因此f[i][j] >= f'[i][j]；
如果第j层中用到的某条边(a, b)应该在比j小的层，假设a是S中的点，b是第j层的点，则在枚举S + {b}时会得到更小的花费，即这种方式枚举到的所有花费均大于等于某个合法生成树的花费，因此f[i][j] <= f'[i][j]
所以有 f[i][j] = f'[i][j]。

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N =12,M=1<<N,INF=0x3f3f3f3f;

int f[M][N];
int n,m;
int d[N][N];
int g[M];

int main()
{
    cin>>n>>m;

    memset(d,0x3f,sizeof d);
    for(int i=0;i<n;i++) d[i][i]=0;

    //为了二进制运用方便，读入点的时候减1，所有的点从0编号到n-1。
    for(int i=0;i<m;i++)
    {
        int a,b,w;
        cin>>a>>b>>w;
        a--,b--;
        d[a][b]=d[b][a]=min(d[a][b],w);
    }

    for(int i=1;i<1<<n;i++)
        for(int j=0;j<n;j++)
            if(i>>j&1)
            {
                for(int k=0;k<n;k++)
                    if(d[j][k]!=INF)
                        g[i]|=1<<k;
            }//i状态下 下一步能去到的状态。

    memset(f,0x3f,sizeof f);
    for(int i=0;i<n;i++)  f[1<<i][0]=0;//只包括第i个点这一个点  代价都为0

    for(int i=1;i<1<<n;i++)
        for(int j=(i-1)&i;j;j=(j-1)&i)//枚举i的非全子集    &同为1才为1->让j不会在在i为0的某一位上是1
            if((g[j]&i)==i)   //j可以去到i
            {
                int remain=i^j;//i比j多包含的点
                int cost=0;
                for(int k=0;k<n;k++)
                    if(remain>>k&1)
                    {
                        int t=INF;
                        for(int u=0;u<n;u++)
                            if(j>>u&1)
                                t=min(t,d[k][u]);
                        cost +=t;//连通两个点能让j->i 的最短路径方案
                    }
                //枚举树高
                for(int k=1;k<n;k++) f[i][k]=min(f[i][k],f[j][k-1]+cost*k);
            }

    int res=INF;
    for(int i=0;i<n;i++)  res=min(res,f[(1<<n)-1][i]);
    cout<<res;
    return 0;
}

作者：yankai
链接：https://www.acwing.com/activity/content/code/content/4156902/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。