数据结构 图

树是无环连通图，是一种特殊的图。

分类

图分为有向图[边是有方向的]和无向图[边是无方向的]。

无向图(a—b)，建立两条有向图(a—>b，b—>a)，无向图是一种特殊的有向图。

存储有向图

邻接矩阵 ——用于存储比较稠密的图【O(n^2)】

开一个二维数组，g[a,b]，a—>b；如果有权重，存权重，如果没有权重，就是布尔值；不能存储重边。

邻接表

n个点，每个点都有一个单链表，每个点的单链表存储该点可以到达的点，单链表内部点的顺序不重要。

//插入a—>b的边，在a所对应的单链表中插入b

void add(int a, int b) {

e[idx] = b;

ne[idx] = h[a];

h[a] = idx++;

}

有向图的遍历

宽度优先遍历

一层一层搜索

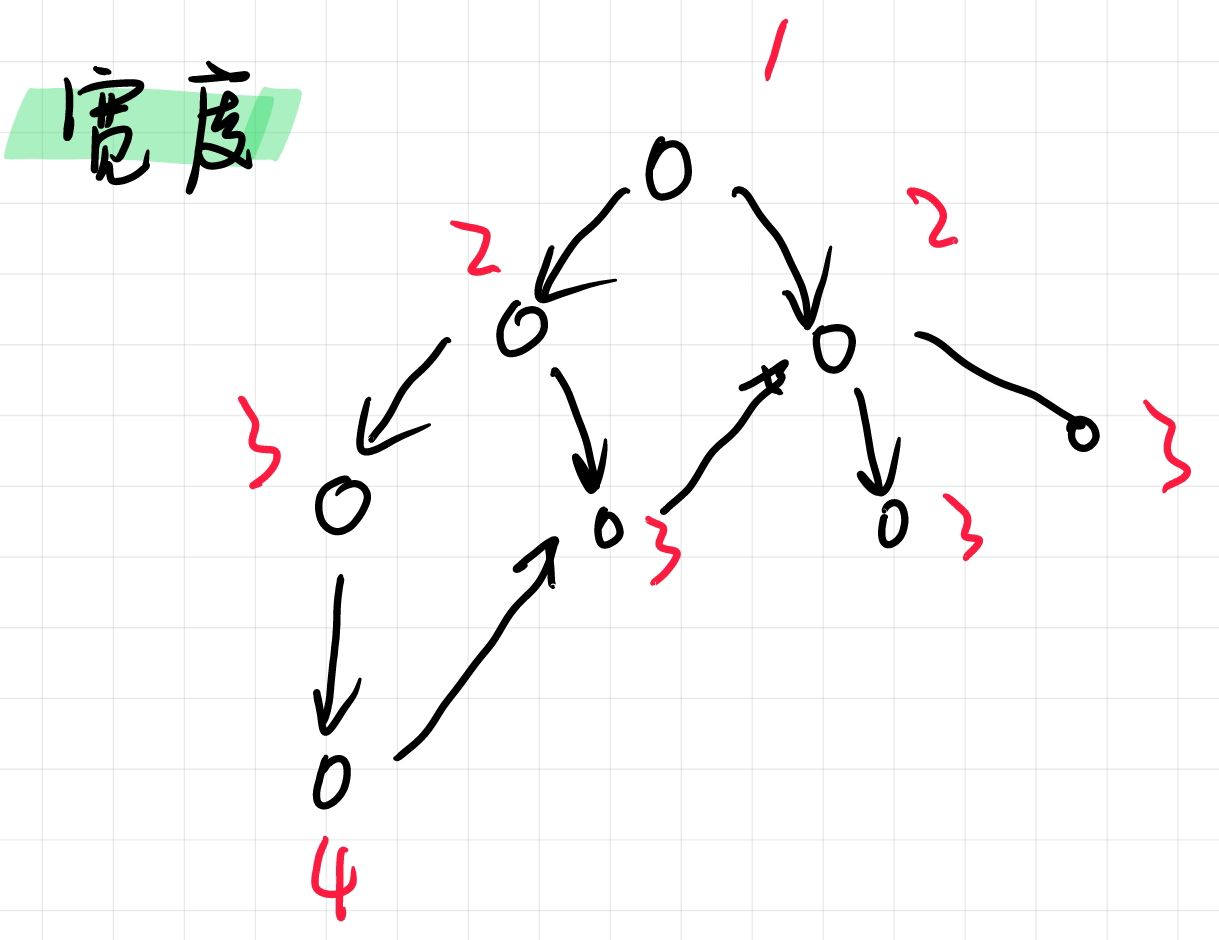
框架

queue ＜——　将起始状态插入队列中，即将1号点插入队列

while （queue 不空）{

t 每次取队头元素

拓展 t 所有能到的点 x

if（x 未被遍历）{

　queue <——x 将 x 入队

d[x]=d[t]+1

}

}

例题——图中点的层次

给定一个n个点m条边的有向图，图中可能存在重边和自环。

所有边的长度都是1，点的编号为1~n。

请你求出1号点到n号点的最短距离，如果从1号点无法走到n号点，输出-1。

输入格式

第一行包含两个整数n和m。

接下来m行，每行包含两个整数a和b，表示存在一条从a走到b的长度为1的边。

输出格式

输出一个整数，表示1号点到n号点的最短距离。

数据范围

1≤n,m≤10^5

输入样例

4 5

1 2

2 3

3 4

1 3

1 4

输出样例

1

代码

#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010;
int n, m;
int h[N], e[N], ne[N], idx;
int d[N], q[N];
void add(int a, int b) {//插入函数
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
int bfs() {
	int hh = 0, tt = 0;
	q[0] = 1;
	memset(d, -1, sizeof d);//初始化距离，-1代表未被初始化
	d[1] = 0;
	while (hh <= tt) {//判断队列是否为空
		int t = q[hh++];//取队头
		for (int i = h[t];i != -1;i = ne[i]) {//扩展队头
			int j = e[i];
			if (d[j] == -1) {
				d[j] = d[t] + 1;
				q[++tt] = j;
			}
		}
	}
	return d[n];
}
int main() {
	cin >> n >> m;
	memset(h, -1, sizeof h);//初始化表头
	for (int i = 0;i < m;i++) {
		int a, b;
		cin >> a >> b;
		add(a, b);
	}
	cout << bfs() << endl;
}

深度优先遍历

找到一个起点，然后从这个 起点开始，一条路走向黑

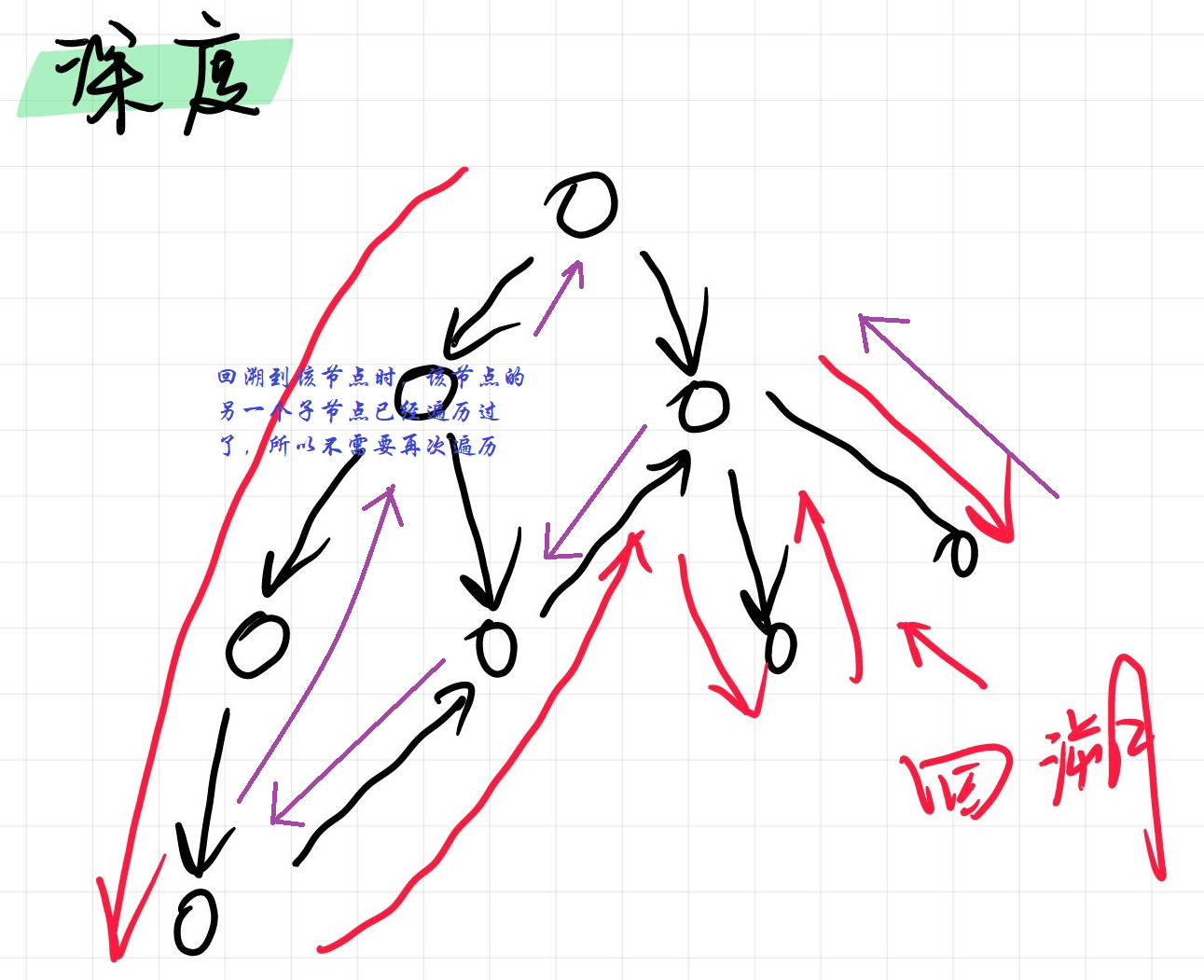
邻接表的深度优先遍历

主函数：

for(int i=0;i<n;i++) dfs(i); //枚举起点

dfs：

利用图中结点的编号进行搜索，e存图中结点的编号

int h[N], e[M], ne[M], idx;//h存n个链表的链表头，e存每个结点的值是多少，ne存每个结点的next值

bool st[N];

//树和图的深度优先搜索

void dfs(int u) {//u是当前dfs到的点

st[u] = true;//标记一下，已经被搜过了

for (int i = h[u];i != -1;i = ne[i]) {//遍历u的所有出边

int j = e[i];//链表中该点在图中的编号

if (!st[j])//如果j没有被搜过，那么就进行搜索

dfs(j);

}

例题——树的重心

给定一颗树，树中包含n个结点（编号1~n）和n-1条无向边【无向图】。

请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。

重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。

输入格式

第一行包含整数n，表示树的结点数。

接下来n-1行，每行包含两个整数a和b，表示点a和点b之间存在一条边。

输出格式

输出一个整数m，表示重心的所有的子树中最大的子树的结点数目。

数据范围

1≤n≤10^5

输入样例

9

1 2

1 7

1 4

2 8

2 5

4 3

3 9

4 6

输出样例

4

代码

#include<iostream>
#include<cstring>
using namespace std;
const int N = 100010, M = N * 2;
int n;
int h[N], e[M], ne[M], idx;//h存n个链表的链表头，e存每个结点的值是多少，ne存每个结点的next值
bool st[N];
int ans = N;//答案，存最小的最大值
//插入a—>b的边，在a所对应的单链表中插入b
void add(int a, int b) {
	e[idx] = b;
	ne[idx] = h[a];
	h[a] = idx++;
}
//树和图的深度优先搜索
int dfs(int u) {//u是当前dfs到的点,返回以u为根的子树中，点的数量【以u为根的子树的大小】
	st[u] = true;//标记一下，已经被搜过了
	int sum = 1, res = 0;//res存删去重心后，每一个连通块大小的最大值；sum存当前子树的大小
	for (int i = h[u];i != -1;i = ne[i]) {//遍历u的所有初边
		int j = e[i];//链表中该点在图中的编号
		if (!st[j]) {//如果j没有被搜过，那么就进行搜索
			int s = dfs(j);//当前子树的大小
			res = max(res, s);//当前子树是一个连通块，所以与之前连通块的最大值进行比较
			sum += s;//以u的子结点为根结点的子树是以u为根结点子树的一部分
		}
	}
	res = max(res, n - sum);
	ans = min(ans, res);
	return sum;
}
int main() {
	cin >> n;
	memset(h, -1, sizeof h);//邻接表初始化，头指向-1
	for (int i = 0;i < n - 1;i++) {
		int a, b;
		cin >> a >> b;
		add(a, b);
		add(b, a);
	}
	dfs(1);//可以从任意点开始搜
	cout << ans << endl;
	return 0;
}

特殊的图——树[无环连通图]

概念

在计算器科学中，树（英语：tree）是一种抽象数据类型或是实现这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

结点

指树中的一个元素；

结点的度

指结点拥有的子树的个数，二叉树的度不大于2；

树的度

指树中的最大结点度数；

叶子

度为0的结点，也称为终端结点；

高度

叶子节点的高度为1，根节点高度最高；

层

根在第一层，以此类推；

特点

一个父结点可以有多个子结点，一个子结点只能有一个父结点，多个子结点对应一个父结点。

①每个节点有零个或多个子节点；

②没有父节点的节点称为根节点；

③每一个非根节点有且只有一个父节点；

④除了根节点外，每个子节点可以分为多个不相交的子树；

二叉树

概念

每个节点最多含有两个子树的树称为二叉树。（我们一般在书中试题中见到的树是二叉树，但并不意味着所有的树都是二叉树。）

性质

1：二叉树的第i层上至多有2^(i-1)个结点

2：深度为k的二叉树，至多有2^k-1个结点

满二叉树

除最后一层无任何子节点外，每一层上的所有节点都有两个子节点。也可以这样理解，除叶子节点外的所有节点均有两个子节点。节点数达到最大值，所有叶子节点必须在同一层上。

完全二叉树

若设二叉树的深度为h，除第h层外，其它各层 (1～(h-1)层) 的节点数都达到最大个数（即节点均满），第h层所有的节点都连续集中在最左边（虽然最下面一层节点不满，但是所有节点在左边连续排列，空位都在右边），这就是完全二叉树。

性质

• 结点 i 的子结点为 2*i 和 2*i+1 (前提是都小于总结点数)
• 结点 i 的父结点为 i/2
• 如果n个节点的完全二叉树的节点按照层次并按从左到右的顺序从0开始编号：

• • 序号为0的节点是根
  • 对于 i>0，其父节点的编号为（i-1）/2
  • 若 2*i+1<n，其左子节点的序号为 2*i+1，否则没有左子节点
  • 若 2*i+2<n，其右子节点的序号为 2*i+2，否则没有右子节点

遍历

深度优先遍历

按照一条路径尽可能的向前探索，直至检查完一个叶节点。

先序和中序可以唯一确定一个树【在先序中找父结点，在中序确定位置，得到左子树和右子树】

中序和后序可以唯一确定一个树【在后序中找父结点，在中序确定位置，得到左子树和右子树】

先序和后序不能唯一确定一个树【不能确定左子树和右子树的情况】

这三种遍历方法只是访问结点的时机不同，访问结点的路径都是一样的，时间和空间复杂度皆为O(n)

先序 根->左子树->右子树

父 左->右

先输出父节点，然后从左到右输出子节点

中序 左子树->根->右子树

先输出左节点，然后输出父节点，最后输出右节点

后序 左子树->右子树->根

先输出左节点，然后输出右节点，最后输出根节点

宽度优先搜索

在所有路径上齐头并进，按照路径长度由近到远访问节点，即按照二叉树的层数逐层访问树中的节点。

例题

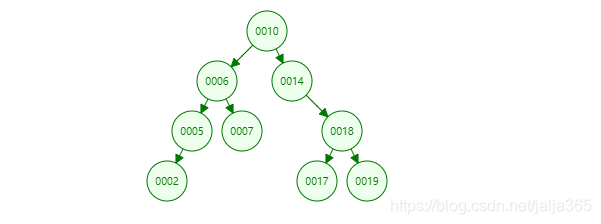
先序：10 6 5 2 7 14 18 17 19

中序：2 5 6 7 10 14 17 18 19

后序：2 5 7 6 17 19 18 14 10

层次：10 6 14 5 7 18 2 17 19

作用

高效地存储和查找字符串集合的数据结构

适用于字符类型不多的字符串

如何存储字符串集合

有一个根节点，但该节点不存放数据。

存储的时候，应该在每个单词的结尾做标记，表示以该字母结尾的结点有一个单词。防止查找时，误以为该树存储了该字符串的子串。例如，树中存储“abcd”，若没有做标记，在查找“abc”是否在树中时，容易误以为该串存在，做标记后，查找到最后一个字符时，应该检测是否有结束标志，若没有则不存在。

如何查找

从根结点开始，挨个字符在对应层上寻找，若找到就继续向下一层找对应的字符，直到找到最后一个字符，观察字符上是否有结束标记，若有则说明该树上存储了该字符串，若是没有则说明该树上没有存储。若是直接没在该层上找到对应的字符，则说明该树上没有存储。

模板

数据含义

• 整型 idx 用于给所有的存入树的字符进行编号，idx = 0 既表示根节点，又表示空节点（根节点不存数据）
• 数组 cnt 用于表示以某个 idx 表示的字符为结尾的字符串的个数
• 二维数组 son 用于存储每个 idx 对应的所有子节点，在 son 中的元素值为0，表示空节点

son 数组中元素的值代表该节点的子节点所在的位置，即 son 数组的高维度的编号。【son[a][b]=c表示该节点的子节点位于son[c]中】例如，先后存入 abc、abcd、abd、bcd。

为什么 son 不能存储每一层的字母，而是使用这种方式存储？

如果 son 存储每一层的字母，则分不清该字母是哪一个节点下的子节点了。

存储

每次存储字符串都是从根节点开始存储。当存储一个字符时，就应该给该字符编号，并根据编号跳到 son 中编号对应的那一层【将一维置为该编号】，该层存储该编号的所有子节点。当存储到字符串的最后一个字符时，应将该字符的编号作为 cnt 数组的下标，令该元素自身数据自增，表示以该编号所表示的字符为结尾的字符串个数+1，即表示该树上存储了多少个相同的字符串。

//存储
void insert(char str[]) {
    int p = 0;//根节点是0
    for (int i = 0;str[i];i++) {//从根节点开始，从前往后遍历
//因为字符串的最后一个字符是空字符，所以可以使用空字符判断该字符串是否到达末尾
        int u = str[i] - 'a';//将“a~z”映射成“0~25”
        if (!son[p][u]){//如果p这个节点不存在u这个儿子，就将其创造出来
            ++idx;
            son[p][u] = idx;//写成son[p][u]=++idx;是未定义行为，一个序列点对应两个副作用
        }
        p = son[p][u];
    }
    cnt[p]++;//表示以p点结尾的单词数多了一个
}

查找——返回字符串出现的次数

查找和存储思路一样，只是发现没存储该字符就直接返回0，表示没存储该字符串，存储该字符时才跳转。

int query(char str[]){
    int p=0;
    for(int i=0;str[i];i++){
        int u=str[i]-'a';
        if(!son[p][u])
            return 0;//不存在该字符串时直接返回0
        p=son[p][u];
    }
    return cnt[p];
}

输出——遍历输出树中所有的字符串

使用 dfs ，将当前的字符编号作为参数传入，表示要遍历该层26个字符，使用一个 string 存储当前遍历所组成的字符串，若遍历到某个字符存在树中，则将其放在 string 的末尾，并检测是否在以该字符编号为结尾的字符串，如果存在则输出。之后以其子节点层数编号作为新的参数执行 dfs 。当26个字符都没有存储在树中，则说明该路径上的所有的字符串遍历完成，应该进行回退，回退到上一层时，应将 string 的最后一个字符删去。之后遍历该层其他字符。

string temp;
void dfs(int p){
    for(int i=0;i<26;i++){
        if(son[p][i]){
            char tp[2]={'a'+i};
            temp.append(tp);
            if(cnt[son[p][i]]){
                cout<<temp<<endl;
            }
            dfs(son[p][i]);
            temp.pop_back();
        }
    }
}

例题——Trie字符串统计

维护一个字符串集合，支持两种操作：

“I x”向集合中插入一个字符串x；

“Q x”询问一个字符串在集合中出现了多少次。

共有N个操作，输入的字符串总长度不超过 10^5，字符串仅包含小写英文字母。

输入格式

第一行包含整数N，表示操作数。

接下来N行，每行包含一个操作指令，指令为”I x”或”Q x”中的一种。

输出格式

对于每个询问指令”Q x”，都要输出一个整数作为结果，表示x在集合中出现的次数。

每个结果占一行。

数据范围

1≤N≤2∗10^4

输入样例

5

I abc

Q abc

Q ab

I ab

Q ab

输出样例

1

0

1

#include<iostream>

using namespace std;

const int N = 100010;

int son[N][26], cnt[N], idx;//下标是0的点，既是根结点，又是空结点

//cnt 存以当前这个点结尾的单词有多少个

char str[N];

//存储

void insert(char str[]) {

int p = 0;

for (int i = 0;str[i];i++) {

int u = str[i] - 'a';

if (!son[p][u])//如果p这个结点不存在u这个儿子，就将其创造出来

son[p][u] = ++idx;

p = son[p][u];

}

cnt[p]++;

}

//查询

int query(char str[]) {

int p = 0;

for (int i = 0;str[i];i++) {

int u = str[i] - 'a';

if (!son[p][u])

return 0;

p = son[p][u];

}

return cnt[p];

}

int main() {

int n;

scanf("%d", &n);

while (n--) {

char op[2];

scanf("%s%s", op, str);

if (op[0] == 'I')

insert(str);

else

printf("%d\n", query(str));

}

return 0;

}