2.1逻辑分类/二元分类 logistic regression
经典问题:
假如你有一张图片作为输入,你想输出能识别此图的标签,也就是:如果是猫,输出1;如果不是猫,输出0。这是老吴最喜欢的猫检测器;
我们用y来表示输出的结果标签;
一张图片在计算机中是如何表示的?计算机保存一张图片,要保存三个独立矩阵,分别对应图片中红、绿、蓝三个颜色通道;如果输入图片是6464像素的,就会有3个64
64的矩阵,分别对应图片中的红、绿、蓝三个通道的像素亮度;
要把这些像素亮度值放进一个特征向量里,就先定义一个特征向量,然后将红色像素矩阵从第一行第一列开始放入,一行放完放下一行,再放绿色矩阵、蓝色矩阵的;
得到的特征向量是一个列向量,很长,它将图片中所有红绿蓝像素强度值都列出来,向量的维度将会是
,用
来表示输入的特征向量
的维度。此处
;
二分分类问题的目标是训练出一个分类器,它以图片的特征向量作为输入,预测输出的结果标签
是1还是0,也就是预测图片中是否有猫。
符号规定:
1. 用一对表示一个单独的样本,
是
维的特征向量,
的值为0或1,即
;
2. 训练集由个训练样本构成,
表示样本1的输入和输出,
表示样本2的,……,
表示最后一个样本
的输入和输出;
3. 如果是训练样本的个数,可以写为;如果是测试样本的个数,可以写为
4. 为了用更紧凑的符号表示训练集,定义一个大写矩阵,由以下构成:
因为都是列向量,所以才如此横向堆放;
有
列,
行,也称矩阵高度是
;
在Python中,命令用于输出矩阵X的维度,即
。
5. 定义一个大写矩阵,由以下组成:
是一个
的矩阵,即
2.2 logistic回归
给定已知的输入特征向量,你需要一个算法可以给出一个预测值
,可以说是对
的预测,正式地讲
是一个概率:当输入特征
满足条件时,
的条件概率,即:
如果是图片,你希望
能告诉你这是一张猫图的概率;
参数是(一个同样为
维的列向量)和
(一个实数);
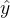 和参数
和参数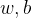 之间的关系是怎样的呢?
之间的关系是怎样的呢?
假设,这样满足
是一个数,但是并未满足
是一个在
之间的概率的要求,一般把这种等式叫线性回归;
所以要引入函数:

定义就确保了
介于0和1之间;
并且函数的导数恒大于0,所以是单增的;
总之,logistic回归里你要做的就是学习参数。
2.3 logistic回归中的损失函数
为了让模型通过学习参数来调整参数,要给一个有个样本的训练集:
希望通过训练集找到合适的参数,来得到你对训练集的预测值
,使它能接近于训练集的标签值
,即尽可能让
;这里右上角带圆括号有数字的上标表示这是第几个样本的数据,后面会有方括号和花括号,要注意区分,剧透一下方括号表示是神经网络第几层的参数,花括号表示mini-batch中第几个子集的数据;
损失函数 Loss function  应该如何定义?
应该如何定义?
如果定义为,当你学习这些参数时,后面讨论优化问题时会发现函数是非凸的,最后会得到很多个局部最优解,在使用梯度下降法时可能找不到全局最优值;当然有人也去研究了非凸函数的优化,建议看看老吴的采访视频,有很多启发;
我们通过定义损失函数来衡量你的预测输出值和实际值
有多么接近,一般设计成损失函数的值越小,代表接近效果越好,常用的logistic回归的损失函数定义为:
一个粗浅的理解是枚举,如果,则
,训练时会往损失函数降低的方向前进,当损失函数尽量小时,
会尽量大,
就会尽量大,而它本身是一个值域为[0,1]的概率,就会使
接近于1,这样就实现了
;如果
,则
,损失函数最小化会使得
尽量小,也就使得
接近于0,同样实现了
;后面会有一节专门分析损失函数是如何设计出来的;
损失函数是在单个样本里定义的,它只衡量在单个训练样本上算法的表现;
成本函数 Cost function 则衡量在全体训练样本上算法的表现,定义为:
所以,要寻找合适的使得
最小。
2.4梯度下降法
一个直观的理解是当简化成一维向量时,
就是在以
为
轴,而
轴代表高度的一个空间曲面,并且是像碗一样的凸曲面,所以理论上来说碗底存在一个点
能够使
达到最小值,这个最小值点也叫全局最优解;

我们要做的就是初始化,然后用梯度下降法一步一步去逼近这个全局最优解,一般是沿最陡的下坡方向去走每一步;在高数里,最陡的方向就是所谓的梯度;
为了简单起见,先忽略参数,这样可以把
看成是
的函数
,并且假定
是一维向量,画在一个二维图中:

只要重复进行以下运算,就能让任何初始点不断向最低点靠近:
其中,是编程时的变量名,它真正的含义是损失函数对w的导数:
而是学习率,
,它控制的是每一次梯度下降法的步长,也就是图中一个箭头走过多远;
能实现的原因:如果初始点在最低点右边,那么导数,进行一次运算就会让
变小从而靠近最低点;如果初始点在最低点左边,那么导数
,进行一次运算就会让
变大从而靠近最低点;
推广到中就可以轻松得到梯度下降法的公式:
注意这里的含义改变了,指的是损失函数分别对
的偏导数:






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








