吴恩达深度学习deeplearning.ai学习笔记（一）3.4 3.6 3.7 3.8

fanfan401

于 2024-08-02 08:55:11 发布

阅读量256

点赞数 3

文章标签：人工智能深度学习学习

本文链接：https://blog.csdn.net/weixin_66188523/article/details/140858971

版权

3.4 多个例子中的向量化

对于m个样本而言，上述步骤要重复m次，即输入 $x^{(1)}$ ，四个等式进行计算，输出 $\hat{y}^{(1)}=a^{[2](1)}$ ；输入 $x^{(2)}$ ，四个等式进行计算，输出 $\hat{y}^{(2)}=a^{[2](2)}$ ； $\cdots$ ；输入 $x^{(m)}$ ，四个等式进行计算，输出 $\hat{y}^{(m)}=a^{[2](m)}$ ；假如使用for loop编程：

版本1：

$for\ i=1\ to\ m:$

$z^{[1](i)}=w^{[1]}x^{(i)}+b^{[1]}$

$a^{[1](i)}=\sigma(z^{[1](i)})$

$z^{[2](i)}=w^{[2]}a^{[1](i)}+b^{[2]}$

$a^{[2](i)}=\sigma(z^{[2](i)})$

如何向量化？先进行定义：

$X=\begin{bmatrix} x^{(1)} &x^{(2)} &\cdots &x^{(m)} \end{bmatrix}$

$Z^{[1]}=\begin{bmatrix} Z^{[1](1)} &Z^{[1](2)} &\cdots & Z^{[1](m)} \end{bmatrix}$

$A^{[1]}=\begin{bmatrix} a^{[1](1)} &a^{[1](2)} &\cdots &a^{[1](m)} \end{bmatrix}$

$Z^{[2]}=\begin{bmatrix} Z^{[2](1)} &Z^{[2](2)} &\cdots & Z^{[2](m)} \end{bmatrix}$

$A^{[2]}=\begin{bmatrix} a^{[2](1)} &a^{[2](2)} &\cdots &a^{[2](m)} \end{bmatrix}$

记住一条原则：横向堆叠就可遍历不同样本；

版本2：Vectorized

$Z^{[1]}=w^{[1]}X+b^{[1]}$

$A^{[1]}=\sigma(Z^{[1]})$

$Z^{[2]}=w^{[2]}A^{[1]}+b^{[2]}$

$A^{[2]}=\sigma(Z^{[2]})$

$w^{[1]},b^{[1]},w^{[2]},b^{[2]},A^{[1]},A^{[2]}$ 这些矩阵的维度怎么判断？

首先从 $X$ 入手， $X=\begin{bmatrix} x^{(1)} &x^{(2)} &\cdots & x^{(m)} \end{bmatrix}$ 显然是 $n_x\times m$ 的矩阵；

$w^{[1]}=\begin{bmatrix} w_1^{[1]T}\\ w_2^{[1]T}\\ \vdots\\ w_{n^{[1]}}^{[1]T} \end{bmatrix}$ ，它的列数是 $n_x=n^{[0]}$ ，而它的行数是 $n^{[1]}$ ，表示第一层的隐藏单元数；

$b^{[1]}=\begin{bmatrix} b_1^{[1]}\\ b_2^{[1]}\\ \vdots\\ b_{n^{[1]}}^{[1]} \end{bmatrix}$ ，它的列数是1，而它的行数是 $n^{[1]}$ ；

$Z^{[1]}=\begin{bmatrix} Z^{[1](1)} &Z^{[1](2)} &\cdots & Z^{[1](m)} \end{bmatrix}$ ，它的列数等于m，它的行数等于 $n^{[1]}$ ；

$A^{[1]}$ 的维数与 $Z^{[1]}$ 保持一致；

$w^{[2]}=w_1^{[2]T}$ ，它的列数等于 $n^{[1]}$ ，它的行数等于1，也等于 $n^{[2]}$ ，是巧合吗？

$b^{[2]}=b_1^{[2]}$ ，是一个数，但是也可以说它的列数是1，而它的行数等于 $n^{[2]}$ ，是巧合吗？

$Z^{[2]}=\begin{bmatrix} Z^{[2](1)} &Z^{[2](2)} &\cdots & Z^{[2](m)} \end{bmatrix}$ ，它的列数等于m，它的行数等于1，也等于 $n^{[2]}$ ；

$A^{[2]}=\begin{bmatrix} a^{[2](1)} &a^{[2](2)} &\cdots &a^{[2](m)} \end{bmatrix}$ ，它的维度与 $Z^{[2]}$ 保持一致；

事实上，即使对于多隐层神经网络，也就是我们常说的深层神经网络而言，我们能够总结出一些普适性的维度规律：

$w^{[l]}$ 的维度必须是 $(n^{[l]},n^{[l-1]})$ ；

$a^{[l]},z^{[l]},b^{[l]}$ 的维度必须是 $(n^{[l]},1)$ ，即使是多样本下对 $a^{[l](i)},i=1,2,\cdots,m$ 之类也一样；

$Z^{[l]},A^{[l]}$ 的维度必须是 $(n^{[l]},m)$ ，且 $A^{[0]}=X$ 的维度就是 $(n^{[0]},m)$ ；

为什么说这四个方程就实现了向量化？

$Z^{[1]}=\begin{bmatrix} Z^{[1](1)} &Z^{[1](2)} &\cdots & Z^{[1](m)} \end{bmatrix}\\=\begin{bmatrix} w^{[1]}x^{(1)}+b^{[1]} &w^{[1]}x^{(2)}+b^{[1]} &\cdots &w^{[1]}x^{(m)}+b^{[1]} \end{bmatrix}$

第一列等于： $\begin{bmatrix} w_1^{[1]T}\\ w_2^{[1]T}\\ w_3^{[1]T}\\ w_{4}^{[1]T} \end{bmatrix}x^{(1)}+\begin{bmatrix} b_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\\ b_4^{[1]} \end{bmatrix}=\begin{bmatrix} w_1^{[1]T}x^{(1)}+b_1^{[1]}\\ w_2^{[1]T}x^{(1)}+b_2^{[1]}\\ w_3^{[1]T}x^{(1)}+b_3^{[1]}\\ w_4^{[1]T}x^{(1)}+b_4^{[1]} \end{bmatrix}$

第m列等于： $\begin{bmatrix} w_1^{[1]T}\\ w_2^{[1]T}\\ w_3^{[1]T}\\ w_{4}^{[1]T} \end{bmatrix}x^{(m)}+\begin{bmatrix} b_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\\ b_4^{[1]} \end{bmatrix}=\begin{bmatrix} w_1^{[1]T}x^{(m)}+b_1^{[1]}\\ w_2^{[1]T}x^{(m)}+b_2^{[1]}\\ w_3^{[1]T}x^{(m)}+b_3^{[1]}\\ w_4^{[1]T}x^{(m)}+b_4^{[1]} \end{bmatrix}$

$w^{[1]}X+b^{[1]}=\begin{bmatrix} w_1^{[1]T}\\ w_2^{[1]T}\\ w_3^{[1]T}\\ w_{4}^{[1]T} \end{bmatrix}\begin{bmatrix} x^{(1)} &x^{(2)} &\cdots & x^{(m)} \end{bmatrix}+\begin{bmatrix} b_1^{[1]}\\ b_2^{[1]}\\ b_3^{[1]}\\ b_4^{[1]} \end{bmatrix}$

通过广播变为 $\begin{bmatrix} w_1^{[1]T}x^{(1)} &\cdots &w_1^{[1]T}x^{(m)} \\ w_2^{[1]T}x^{(1)} &\cdots &w_2^{[1]T}x^{(m)} \\ w_3^{[1]T}x^{(1)} &\cdots &w_3^{[1]T}x^{(m)} \\ w_4^{[1]T}x^{(1)} &\cdots & w_4^{[1]T}x^{(m)} \end{bmatrix}+\begin{bmatrix} b_1^{[1]} &\cdots &b_1^{[1]} \\ b_2^{[1]} &\cdots &b_2^{[1]} \\ b_3^{[1]} &\cdots &b_3^{[1]} \\ b_4^{[1]} &\cdots &b_4^{[1]} \end{bmatrix}$

显然加起来以后， $w^{[1]}X+b^{[1]}$ 的第一列和 $Z^{[1]}$ 的第一列相一致，验证二者第m列也一致，由于m可以变化，所以具有普适性，证明 $Z^{[1]}=w^{[1]}X+b^{[1]}$ ，也就证明这实现了对m个样本的向量化

笔者虽然证明了 $Z^{[2]}=w^{[2]}A^{[1]}+b^{[2]}$ 实现了向量化的原因，但就不放在这了；

3.6 激活函数

并不总是用 $\sigma$ 函数，一般形式应该写为：

$a^{[1]}=g^{[1]}(z^{[1]})$

$a^{[2]}=g^{[2]}(z^{[2]})$

主要有四类激活函数： $\sigma$ 函数、 $tanh$ 函数、 $ReLu$ 函数、 $Leaky\ ReLu$ 函数；

什么时候使用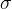 $\sigma$ 函数进行激活？

只有在做二元分类问题时，才会仅仅在输出层使用 $\sigma$ 函数进行激活；

什么时候使用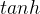 $tanh$ 函数进行激活？

它的激活效果总是优于 $\sigma$ 函数；

$tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$

它实际上就是 $\sigma$ 函数的图像进行平移和伸缩变换以后的图像；

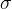它的学名叫双曲正切函数，输出介于-1到1之间，激活函数的平均值更接近于0，有类似于数据中心化的效果，能够使下一层更简单，所以效果优于 $\sigma$ 函数；

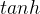$\sigma$ 函数和 $tanh$ 函数共有的缺点是什么？

当 $z$ 很大或很小时，导数非常小，接近于0，此时会大幅降低梯度下降法的效率；

什么时候用 $ReLu$ 函数进行激活？

如果不确定隐层要用什么激活函数，那么默认用 $ReLu$ 函数即可；

虽然 $ReLu$ 函数当 $z<0$ 时导数为0，但实际中是有可能避免这个缺点的；

$Leaky\ ReLu$ 函数只是在 $ReLu$ 函数基础上，当 $z<0$ 时修改了一下，使得其导数不再为0，而是一个很小的数，默认是0.01；

使用 $ReLu$ 函数，神经网络的学习速度会加快很多，因为有相当大的 $z$ 空间导数一直为1不会衰减，更不会出现斜率接近于0时减慢学习速度的效应。

3.7 为什么需要非线性激活函数？

如果全是线性激活函数比如 $g^{[1]}(z)=z,g^{[2]}(z)=2z$ ，那么模型的输出 $y$ 或 $\hat{y}$ 就仅仅是输入特征 $x$ 的线性组合，无论隐藏层多深都改变不了这一点；数学上，两个线性函数的组合依然只是线性函数；几乎只有在应用机器学习的回归问题时才可能在输出层的节点使用线性激活函数，其他都不会考虑使用；注意 $ReLu$ 函数是非线性的；

3.8 激活函数的导数

$If\ a=g(z)=\sigma(z)=\frac{1}{1+e^{-z}}$

$then\ {g}'(z)=a(1-a)$

$If\ a=g(z)=tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}$

$then\ {g}'(z)=1-a^2$

这意味着如果对于 $\sigma$ 函数和 $tanh$ 函数，如果求出了 $a=g(z)$ ，就能够快速求导；

$If\ a=g(z)=ReLu(z)=max\{0,z\}=\left\{\begin{matrix} z,z>0\\ 0,z\leqslant 0 \end{matrix}\right.$

$then\ {g}'(z)=\left\{\begin{matrix} 0,z<0\\ 1,z>0\\ no\ define,z=0 \end{matrix}\right.$

可以认为定义 $z=0$ 处的导数值，但几乎没有影响；

$If\ a=g(z)=Leaky\ ReLu(z)=max\{0.01z,z\}=\left\{\begin{matrix} z,z>0\\ 0.01z,z\leqslant 0 \end{matrix}\right.$

$then\ {g}'(z)=\left\{\begin{matrix} 0.01,z<0\\ 1,z>0\\ no\ define,z=0 \end{matrix}\right.$