2.11 向量化
什么是向量化?通过两个例子说明:
例1:计算
注意:指令对两个一维数组而言,求的是它们的内积;
例2:举一个例子说明向量化使计算速度提升
#按下Shift和enter可执行上述代码,屏幕显示[1,2,3,4];
#生成两个百万维度的数组,直接计算内积,耗时约1.5ms;
#结果for loop 耗时约450ms,用了接近300倍的时间。
2.12 向量化的更多例子
例3: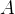 是一个
是一个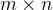 矩阵,
矩阵,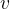 是一个
是一个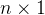 向量,试求
向量,试求
注意指令对两矩阵而言求的是矩阵乘法;
例4:假设内存中已有一个向量 ,求
,求
例5:修改版本2的程序
对于(1)处,由于可以令,因此直接让
初始化为0矩阵,就相当于初始化了
,即:
(2)处则是要实现这
个式子,现在已经定义了
,于是:
这一个式子就等效代替了上面个式子,因为:
(3)处直接改为;
(4)处直接改为
版本3:
2.13 向量化logistic回归
版本3的(1)处要做共
次操作,因此先定义:
(1)处的这m次操作可以由一行代码代替:
原因如下:
首先:
是一个
维行向量,
都是
维列向量,由矩阵乘法可知
和任何一个
相乘都将是一个数,且
矩阵相乘出来是一个
的矩阵
更加详细、严谨的证明是:
其次:
在Python中会通过广播自动地将实数
扩展为
矩阵
,即:
最后:
就相当于完成了所需的次操作;
编程时,用
表示
转置后的矩阵,用
表示两矩阵相乘;
(2)处定义 ,即可用一行式子代替:
,即可用一行式子代替:
因为:
(3)处要做 共
共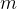 次操作,定义矩阵:
次操作,定义矩阵:
于是用一行代码就可以代替上面次操作:
因为:
(4)处要做 共m次相加操作,且考虑后面要进行
共m次相加操作,且考虑后面要进行 ,可用一行式子代替:
,可用一行式子代替:
因为:
并且都是数;
最后结合上就变为
。
(5)处要做 共m次相加,即:
共m次相加,即:
实际上,对于矩阵而言,使用元素求和指令
就可以实现对这
个数求和,结合
,用一行代码就可以替代:
版本4:(一次梯度下降的最终版本)
这仅仅完成了一次梯度下降,要实现多次梯度下降应该在最外层加上一个不可省略的for loop来进行一定次数的梯度下降:
就是执行1000次这样的梯度下降。
2.15 Python中的广播
Python对两个矩阵(也可以是实数)做加减乘除时,遇到尺寸不一样的情况,会自动成行成列copy形成一样尺寸的矩阵,然后再逐元素进行加减乘除。
2.16 关于Python_numpy向量的说明
不要使用去生成一个向量,因为当你用
查看它时会发现:
这就是说它是一个秩为1的数组,既不是行向量,也不是列向量,无法准确地对它进行转置、求外积、求内积……
应该使用以下两种:
用生成一个5维的列向量;
用生成一个5维的行向量;
如果不确定一个向量的维度,可以用assert函数,运行很快,多用就好:
它会计算表达式,如果其值为假(即0),那么它会先向stderr打印出一条出错信息,然后调用abort来终止程序的运行;
如果不可避免地得到一个数组,可以用来把它转为5维列向量,行向量的转法也是类似的。
2.17 logistic损失函数的解释
对于损失函数如何解释?
希望尽量大且能最小化
,故定义:
而对于成本函数如何解释?
要使最大且能最小化
,故定义:





















 1122
1122

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








