【负荷预测】基于灰色理论负荷预测的应用研究（Matlab代码实现）-CSDN博客

本文链接：https://blog.csdn.net/weixin_67304359/article/details/148061063

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于灰色理论负荷预测的应用研究

一、灰色理论的基本原理与适用性

二、灰色理论在负荷预测中的应用场景与优势

三、GM(1,1)模型的构建步骤与改进方法

四、实际应用案例与效果评估

五、灰色理论的局限性及研究进展

六、总结与展望

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

参考文献：

基于灰色理论负荷预测的应用研究

负荷预测是电力系统规划和运行中的重要工作之一，它决定了发电、输电和电量的分配，在一定规划期内负荷与用电量的大小决定了电力系统的发展规划和发展速度。
目前，负荷预测方法很多，其中灰色预测是一种比较有效的方法，而且广泛用于中长期负荷预测中。本文对灰色系统GM(1,1）预测模型及其在负荷预测中的应用进行讨论，并且对如何提高模型的预测精度进行分析。

一、灰色理论的基本原理与适用性

灰色系统理论由邓聚龙于1982年提出，其核心是处理“部分信息已知、部分信息未知”的“小样本”系统。灰色理论通过 累加生成（1-AGO） 将原始数据序列转化为规律性更强的序列，建立微分方程模型（如GM(1,1)）进行预测。其核心思想是通过有限数据挖掘系统内在规律，适用于电力负荷这类数据量少、波动性高、影响因素复杂的场景。

二、灰色理论在负荷预测中的应用场景与优势

适用场景
- 数据贫乏场景：仅需4个以上数据点即可建模，适合早期电力规划或新兴区域。
- 指数增长趋势：对电力负荷的长期增长趋势（如年均增长5%~10%）预测效果显著。
- 短期预测：通过改进模型（如残差修正、新陈代谢模型）可提升短期波动预测精度。
核心优势
- 计算效率高：模型参数通过最小二乘法快速求解，运算复杂度低。
- 抗干扰能力：通过数据平滑、累加生成减弱随机噪声影响。
- 灵活改进：可与马尔科夫链、神经网络等结合，适应复杂场景。

三、GM(1,1)模型的构建步骤与改进方法

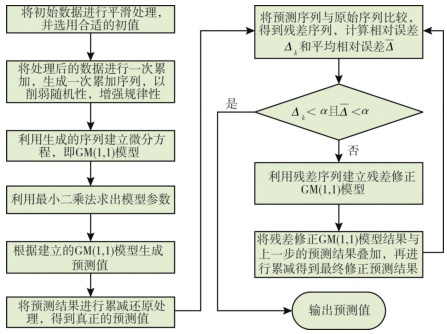
基础模型构建流程
改进方法
- 数据平滑处理：采用滑动平均法或指数平滑法减少异常值干扰。
- 残差修正：对预测误差序列建立残差GM(1,1)模型，二次修正预测结果。
- 参数优化：使用遗传算法或粒子群算法替代最小二乘法，提升模型适应性。
- 组合模型：结合灰色Verhulst模型（适用于饱和趋势）和马尔科夫链（处理随机波动），形成线性组合模型。

四、实际应用案例与效果评估

案例1：改进GM(1,1)模型的中长期预测
- 方法：对某地区2014-2022年负荷数据进行平滑处理，选择最新数据作为初始值，结合残差修正。
- 结果：误差控制在5%以内（E线路除外），较传统模型精度提升30%。
案例2：灰色-马尔科夫组合模型
- 方法：利用灰色Verhulst模型捕捉S型增长趋势，马尔科夫链修正随机波动。
- 结果：某省级电网中长期预测误差低于3%，优于单一模型。
误差分析
- 主要误差来源：数据灰度（离散程度）、非指数增长规律、季节性波动。
- 评估指标：后验差检验（C值<0.35为一级模型）、平均相对误差（MAPE）。

五、灰色理论的局限性及研究进展

局限性
- 指数依赖性：负荷增长不符合指数规律时精度骤降。
- 长期预测偏差：长期预测易高估，需结合弹性系数法校正。
- 多因素耦合：难以直接反映气温、政策等外部因素影响。
近年研究进展
- 混合模型：与ARIMA、Kalman滤波器结合，处理周期性和突变负荷。
- 动态权重优化：自适应调整背景值权重，最小化预测误差。
- 大数据融合：在灰色框架下引入外部数据（如经济指标），扩展信息维度。

六、总结与展望

灰色理论在负荷预测中展现出独特的小数据建模能力，尤其适合电力系统早期规划和短期调度。未来研究可聚焦：

多源数据融合：整合气象、社会活动等实时数据，提升模型外推能力。
智能算法深度结合：利用深度学习优化灰色模型参数与结构。
工程化工具开发：封装改进模型为标准化软件模块，降低应用门槛。

通过理论与实践的持续迭代，灰色理论将在电力系统智能化进程中发挥更重要的作用。

📚2 运行结果

部分代码：

for i=1:(b-1)
yuc(i)=l*exp(-h*i)+j;
end %预测模型表达式
yuc;
x0(1,1);
yuce=[x0(1,1) yuc]; %没有累减时的预测值
for i=1:b-1
yce(i)=yuce(1,i+1)-yuce(1,i);
end
yce; %缺少第一个数据的预测数列
x0(1,1);
ycz=[x0(1,1) yce]; %最终预测值(只是对原数据的拟合值)
ycz;
for i=1:b %后验差校验
cancha(i)=x0(i)-ycz(i);
end
cancha; %残差（初始值-预测值）
x2=mean(x0); %初始值的平均值
x3=mean(cancha); %残差平均值
s=sum((x0-x2).^2)/b; %实际值方差
t=sum((cancha-x3).^2)/b; %残差方差
s1=sqrt(s); %实际值均方差
s2=sqrt(t); %残差均方差
m=s2/s1; %后验差比值即预测值与实际值的离散程度（越小越好）
s0=0.6745*s1; %给定值0.6745s1
p1=abs(cancha-x3); %小误差 p=p{|ε(k)-ε平均值|<0.6745s1}
n=0; %计算p1<s0的个数n
for i=1:b
if p1(i)<s0
n=n+1;
else n=n;
end
end
n;
p=n/b; %小误差概率（越大越好）
if p>0.95&m<0.35
%预测精度好(一级)')
H=0;
elseif p<=0.7&m>=0.65
%预测精度不合格,进行模型改进')
H=1;

ca0=abs(cancha(1:b-2));
x11=cumsum(ca0);
b1=length(ca0);
for i=1:b1-1
ave1(i)=1/2*(x11(i)+x11(i+1));
end
ave1 ;
z1=ave1'; %平均值 @取0.5
a1=ones(b1-1,1);
B1=[-z1,a1] ; %数据矩阵B
Y1=ca0;
Y1(:,1)=[] ; %数据向量（由矩阵x0删除第一列得）
c1=B1'; %g=inv((B'B))B'Y (求解a u)
s1=c1*B1;
d1=inv(s1);
f1=d1*c1;
g1=f1*Y1'; %g=(a,u)'
h1=g1(1,1); %h实际为a
u1=g1(2,1);
j1=u1/h1 ; %预测值=（x(1)-u/h）e +u/h
k1=ca0(1,1);
l1=k1-j1;
for i=1:(b1-1)
yuc1(i)=l1*exp(-h1*i)+j1;
end %预测模型表达式
yuc1;
ca0(1,1);
yuce1=[ca0(1,1) yuc1]; %没有累减时的预测值
for i=1:b1-1
yce1(i)=yuce1(1,i+1)-yuce1(1,i);
end
yce1; %缺少第一个数据的预测数列
ca0(1,1);
ycz1=[ca0(1,1) yce1] ; %最终预测值(只是对原数据的拟合值)
ycz1;
o1=1; %input('输入预测个数')
for i=b1:b1+o1-1
yuc1(i)=l1*exp(-h1*i)+j1;
end
yuc1;
yucezhi11=yuc1(b1-1:b1+o1-1) ; %没有累减时的未来预测值
for i=1:o1
yucezhi21(i)=yucezhi11(i+1)-yucezhi11(i);
end
yucezhi21 ; %最终预测值

elseif p>0.8&m<0.5
%'预测精度合格（二级）')
H=0;
else
%'预测精度勉强合格')
H=0;
end
o=1;%input('输入预测个数');
for i=b:b+o-1
yuc(i)=l*exp(-h*i)+j;
end
yuc;
yucezhi1=yuc(b-1:b+o-1); %没有累减时的未来预测值
for i=1:o
yucezhi2(i)=yucezhi1(i+1)-yucezhi1(i);
end
yucezhi2 ; %最终预测值
else %级比不满足要求，进行数据处理
for i=1:b
y0(i)=log10(log10(x0(i)));
end
H=2;
y0; %进行两次对数处理后的原始数列
end
switch H
case 0
yc=yucezhi2;
case 1
yc=yucezhi21+yucezhi2; %最最终预测值
case 2
yc=mean(x0);
end