AcWing 1087. 修剪草坪（背包模型 + 单调队列优化）

一、问题

二、分析

1、思路

这道题其实类似于背包问题，有两处不同点，一个是本题没有体积的限制，也就是说没有规定我们选多少牛。第二个就是我们选的牛中，不能有$k+1$个及以上头牛是相邻的。

那么既然类似于背包问题的话，我们既可以根据第$i$个选或者不选来写方程。

2、状态表示

$f[i]$表示从前$i$头牛中选，所能达到的最大效率。

3、状态转移

由于我们的$f[i]$是最大值，也就是说我们需要找出所有能转移到$f[i-1]$的表达式，然后在所有的表达式中比较出一个最大值。

如果画成图的话，可以表示为下图：

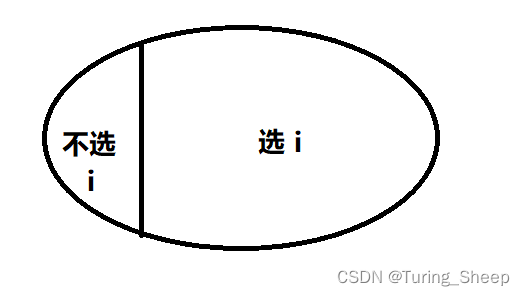
上图的两种情况就是所有能转移到$f[i]$的情况。

对于不选$i$的情况，我们可以表示为$f[i-1]$

但是对于选$i$的情况，我们很不好表示。

因为我们选了第$i$头牛的时候，还需要考虑和它相邻的是否超过了$k$个，也就是说我们无法用一种情况去表示出右面。

那么究其原因就是因为右边的划分过于宽泛，以至于无法用一个转移式子直接表示出来。

因此，我们需要对右边继续细分。

我们的状态定义是前$i$个牛中选的最大效率。也就是说$i$是最后一个牛。

那么能和第$i$个牛连续的，都在$i$的左边。

不能超过$k$个连续的，也就是说最多1，2，3，4，…，k个牛连续。

我们可以按照连续的牛的个数对右侧的集合继续划分。

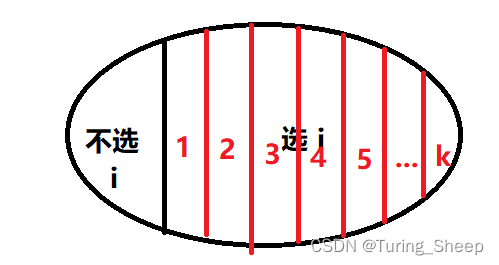
如上图所示，那么我们假设和$i$被连续选中的牛有$j$个，这种情况如何表示呢？

我们看下面的图：

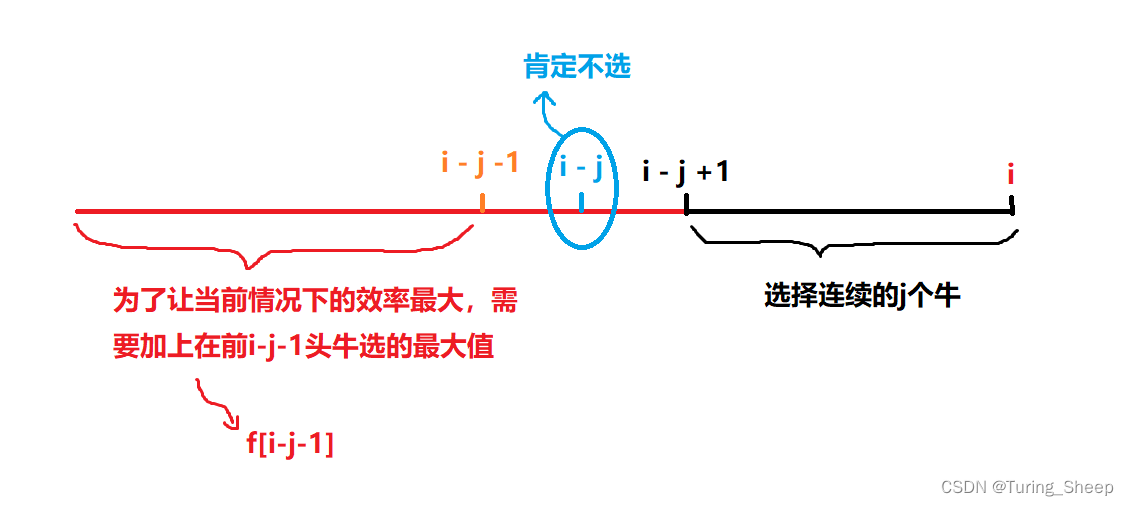
对于黑色区域中，是我们必定选的$j$个连续的牛。

那么现在的关键就是求出这个区间内的牛的效率的和。为了快速的求出来，我们可以使用前缀和。

也就是$s[i]-s[i-j]$

由于蓝色部分肯定不选，所以不用管他。

红色部分则需要用到子问题的最优解，$f[i-j-1]$。

那么我们$f[i]$中连续选$j$头牛的情况就可以表示为：
$$f[i]=f[i-j-1]+s[i]-s[i-j]$$

我们的$j$的范围是$1\le j\le k$的。

我们只需要枚举出每一个$j$的情况，然后求一个最大值。

$$f[i]=max(f[i-j-1]+s[i]-s[i-j])$$

但这个最大值不一定是当前状态的最优解，这个只是刚刚的集合中右半部分的最大值，我们还需要和左半部分的$f[i-1]$做一个比较，选择最大的。

那么我们考虑一下边界情况。

第一个就是要保证$i-j$大于等于0，这个情况对应的实际意义如下：

我们的$j$是$i$左边的连续的$j$头牛，但是有可能我们的$i$比较小，所以不足以提供$j$头牛。

那么这种情况下我们最多选$i$头，只需要写成$s[i]-s[0]$即可。

那么还有一个边界情况。就是我们的$i-j-1\ge 0$

这个边界情况对应的实际意义是：可能我们的左边有$j$头牛，我们算上$i$需要再选$j-1$头牛，也就是说此时只剩下最左边的那一头牛。这时候，这头牛肯定是不选的，即我们刚刚图中的蓝色点。

这种情况下我们的$f[i-j-1]$是不存在的，因为最左边的牛的左边没有牛了。此时我们只需要加上$0$即可。

当$i-j-1$是负数的时候，其实也是蓝色点左侧没有牛的情况，也是替换成0，那么为了方便，直接将$f[0]$初始化为0，然后直接加$f[0]$即可。

我们此时就能写出代码：

#include<bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
ll a[N];
ll f[N];
void solve()
{
	int n, k;
	cin >> n >> k;
	for(int i = 1; i <= n; i ++ )
	{
		scanf("%lld", a + i);
		a[i] += a[i - 1];
	}
	for(int i = 1; i <= n; i ++ )
	{
		f[i] = f[i - 1];
		for(int j = 1; j <= k; j ++ )
		{
		    if(i - j < 0)
		    {
			    f[i] = max(f[0] + a[i] - a[0] , f[i]);
		    }
		    else if(i - j < 1)
			    f[i] = max(f[0] + a[i] - a[i - j], f[i]);
			else
			    f[i] = max(f[i - j - 1] + a[i] - a[i - j], f[i]);
		}
	}
	cout << f[n] << endl;
}
int main()
{
	solve();
	return 0;
}

但是很明显，这样做的时间复杂度是$O(n\ast k)$的，很容易超时。

那么怎么办呢？

我们看下面的优化方案：

4、单调队列优化

根据上面图片的推导，$j$的范围是固定的，那么$i-j$的范围长度也是固定的，但是$i$在改变，所以这个区间范围在向右边挪动。

也就是说，这是一个滑动窗口求最值得问题。

单调队列的复杂度均摊到每一次的操作中是$O(1)$的，那么总的时间复杂度就是$O(n)$

我们还需要注意一个边界问题，对于任意的$x$，我们构造的$g$函数是
$g(x)=f[x-1]-s[x]$

如果$x=0$的话，我们的$f[i-1]$的下标就越界了。

此时我们需要考虑一下实际意义特判一下，如果$x$是0，即$i-j$是0，而$i-j$是我们分析的蓝色点，说明蓝色点的左边没有牛，也就是说$f[i-j-1]$等于0，而$s[0]$也是0，所以当$x=0$的时候，返回$0$就行。

还需要考虑一个问题，一开始的时候队列是空的，也就是我们的$i$等于的时候，此时元素只有一个，那么最大效率就是$s[1]$，就是说前面的那一项是$g[0]$，所以我们要先入队一个$0$。

三、代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
ll f[N], s[N];
ll q[N], hh, tt = -1;
ll g(int x)
{
	if(!x) return 0;
	else return f[x - 1] - s[x];
}
void solve()
{
	int n, k;
	cin >> n >> k;
	
	for(int i = 1; i <= n; i ++ )
	{
		scanf("%d", s + i);
		s[i] += s[i - 1];
	}

	q[++tt] = 0;
	
	for(int i = 1; i <= n; i ++ )
	{
		if(hh <= tt && q[hh] < i - k )hh ++;
		while(hh <= tt && g(q[tt]) <= g(i))tt --;
		f[i] = max(f[i - 1], g(q[hh]) + s[i]);
		q[++tt] = i;
	}
	cout << f[n] << endl;
}
int main()
{
	solve();
}