代码随想录算法训练营第二天 | 977.有序数组的平方 209.长度最小的子数组 59.螺旋矩阵

977.有序数组的平方

https://leetcode.cn/problems/squares-of-a-sorted-array/

1.暴力解法

       直接把给定的数组的元素全部平方完，赋值给原来的数组，利用sort函数将平方完的数组进行排序即可。

2.双指针法

        因为题目给定的其实是一个有序数组，所以平方值其实是从左边和右边逐渐向中间靠拢变小的过程，因为最左边的是负数，越在左边绝对值越大，最右边的是正数，越在右边绝对值越大。

        因此，我们可以设置两个指针（比喻，其实只是数组的下标），一个指向最左边，一个指向最右边，设置k为数组的长度值减一，即数组最右边的下标。然后比较两个指针所指向值的绝对值的大小（其实也就是平方值的大小），如果左边的大于等于右边的，那么左边的值放入结果数组的k所在的位置，k--，同时，左边指针向右移动；如果右边的大于等于左边的，那么右边的值放入结果数组的k所在的位置，k--，同时，右边指针往左移动。

        注意，循环条件应该是left<=right,因为当left==right时，这时候只有一个元素，但是因为咱们的判断条件有右边的大于等于左边的就把值放进去，所以这个等于号会把最后的一个元素放入数组里面。

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) 
{
//暴力解法
// for(int i=0;i<nums.size();i++)
// {
//     nums[i]=nums[i]*nums[i];
// }
// sort(nums.begin(),nums.end());
// return nums;
int k=nums.size()-1;
vector<int>result(nums.size(),0);
for(int i=0,j=nums.size()-1;i<=j;)
{
    if(nums[i]*nums[i]<=nums[j]*nums[j])
    {
     result[k--]=nums[j]*nums[j];
     j--;
    }
    else
    {
        result[k--]=nums[i]*nums[i];
        i++;
    }
}
return result;
    }
};

209.长度最小的子数组

https://leetcode.cn/problems/minimum-size-subarray-sum/

1.暴力解法（会超时）

        因为要找到长度最小的连续的子数组，所以暴力解只需要两个for循环，当i等于0，j不断移动，看看到哪里总和大于target，记录这时候的长度，记录完后，i向后移一位，还是同样的方法，如果长度小于之前记录的值就更新。

2.滑动窗口法

        滑动窗口是只用一个指针j来移动，j从数组的第一个元素开始移动，到sum>target时停下，记录这时候的长度，紧接着，i也可以向右移动了，这里巧妙的点在于因为j所到达的位置是j前面的元素j-1+j-2+...加起来才>sum的位置，所以对于i+1，i+2,...到j-1这个区间的起点而言，它们的最小长度都是会大于从它们的位置到j这段距离，所以这时候i可以不断移动，如果i向右移动后的结果sum还是大于target，说明有更小的区间可以更新范围，如果i向右移动后sum不是大于target，这时候j就可以向右移动了，因为说明从这时的i到还没开始移动的j是不存在sum大于target的数组的，所以这时候j就可以向右探索新的区间。

        这种方法的灵魂之处在于它会自动剔除掉一些不必要的操作，比如既然i到j之间sum>target，那么i+1到j-1之间不存在sum>target的数组，所以i就可以往后走（因为已经可以保障从现在的i到最j已经是可能的最小的区间了）

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
    //暴力解-超时
    //   int result=INT32_MAX;int sum=0;
    //   for(int i=0;i<nums.size();i++)
    //   {
    //         sum=0;
    //         for(int j=i;j<nums.size();j++)
    //         {
    //             sum+=nums[j];
    //             if(sum>=target)
    //             {
    //                 result=j-i+1<result?j-i+1:result;
    //                 break;
    //             }
    //         }
    //   }
    //     return result==INT32_MAX?0:result;
    //滑动窗口
    int sum=0;int result=INT32_MAX;int i=0;
    for(int j=0;j<nums.size();j++)
    {
            sum+=nums[j];
            while(sum>=target)
            {
                result=j-i+1<result?j-i+1:result;
                sum-=nums[i++];
            }
    }
    return result==INT32_MAX?0:result;
    }
};

59.螺旋矩阵

https://leetcode.cn/problems/spiral-matrix-ii/

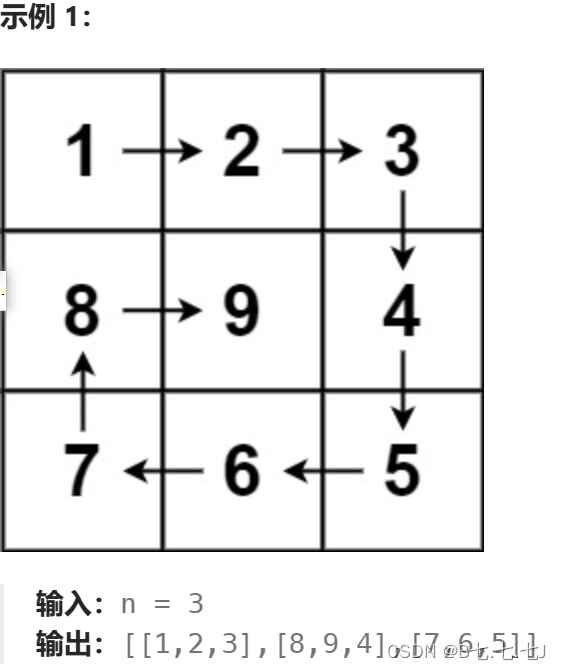
        螺旋矩阵其实就是找增序的路径，随着顺序的增大，对应位置存放对应的数字，存放顺序是（以上图为例）就是从1到2,3到4,5到6,7到8，通过i（表示x坐标）和j（表示y坐标）来表示对应的位置，以1-2为例，i=startx,只有j++到n-2(写成代码是j<n-1);而3-4，j不变，i++到n-2(写成代码是i<n-1)；对于5-6，i不变，j--到>starty；对于7-8，j不变，i--到>startx.

        注意，由于咱们要保证i和j会随着递增改变（比如5-6的时候，因为前面的i已经++到对应那一行了，所以不需要作出多余的改变），所以我们需要把i和j设成for循环外部的全局变量（相对而言 的全局变量）

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) 
{
    vector<vector<int>>res(n,vector<int>(n,0));
    int startx=0;int starty=0;int offset=1;int loop=n/2;
    int count=1;int i;int j;
    while(loop--)
    {   i=startx;j=starty;
        for(j=starty;j<n-offset;j++)
        {
            res[startx][j]=count++;
        }
        for(i=startx;i<n-offset;i++)
        {
            res[i][j]=count++;
        }
        for(;j>starty;j--)
        {
            res[i][j]=count++;
        }
        for(;i>startx;i--)
        {
            res[i][j]=count++;
        }
        startx++;
        starty++;
        offset++;
    }
    if(n%2==1)
    {res[n/2][n/2]=count;}
    return res;
 }
};