第14届:



第13届:

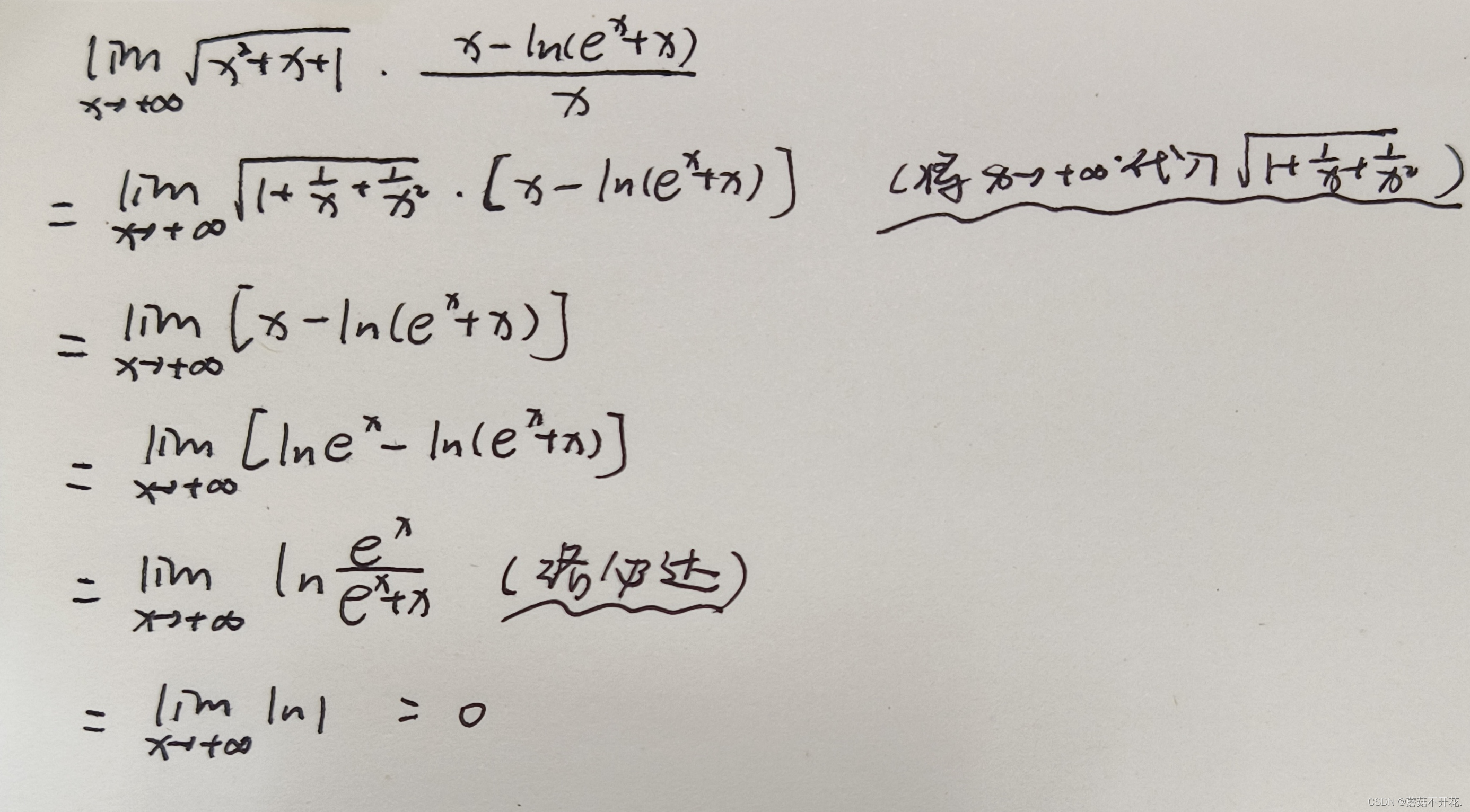
第12届:

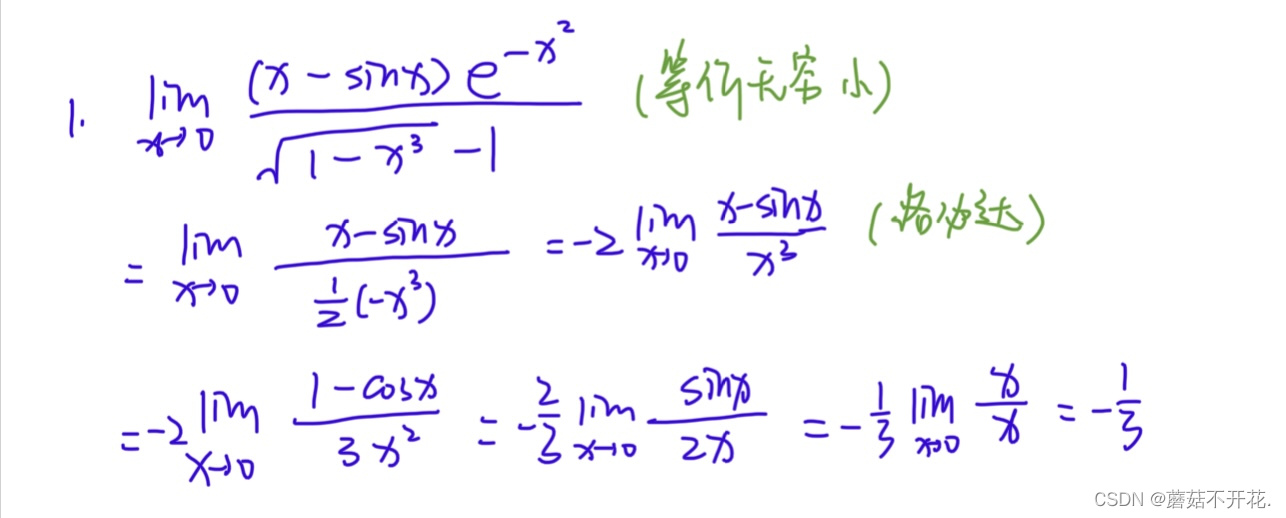
注:此处的等价无穷小为1,详细可见上一篇文章。
第11届:


第10届:
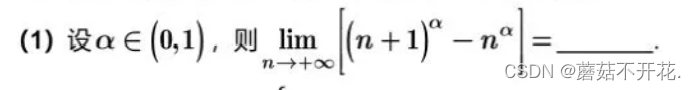

第9届:
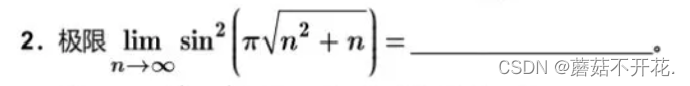
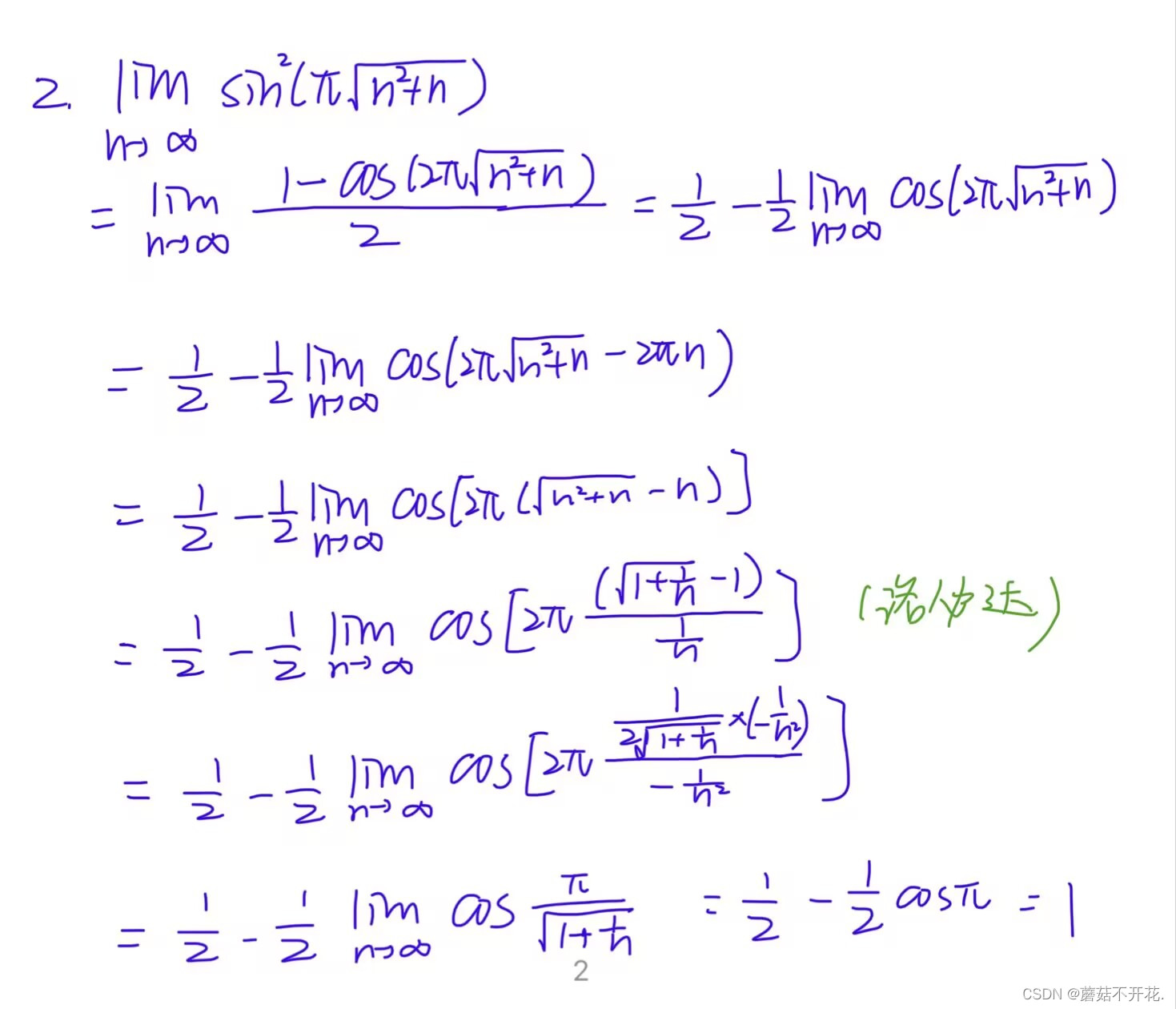
第8届:

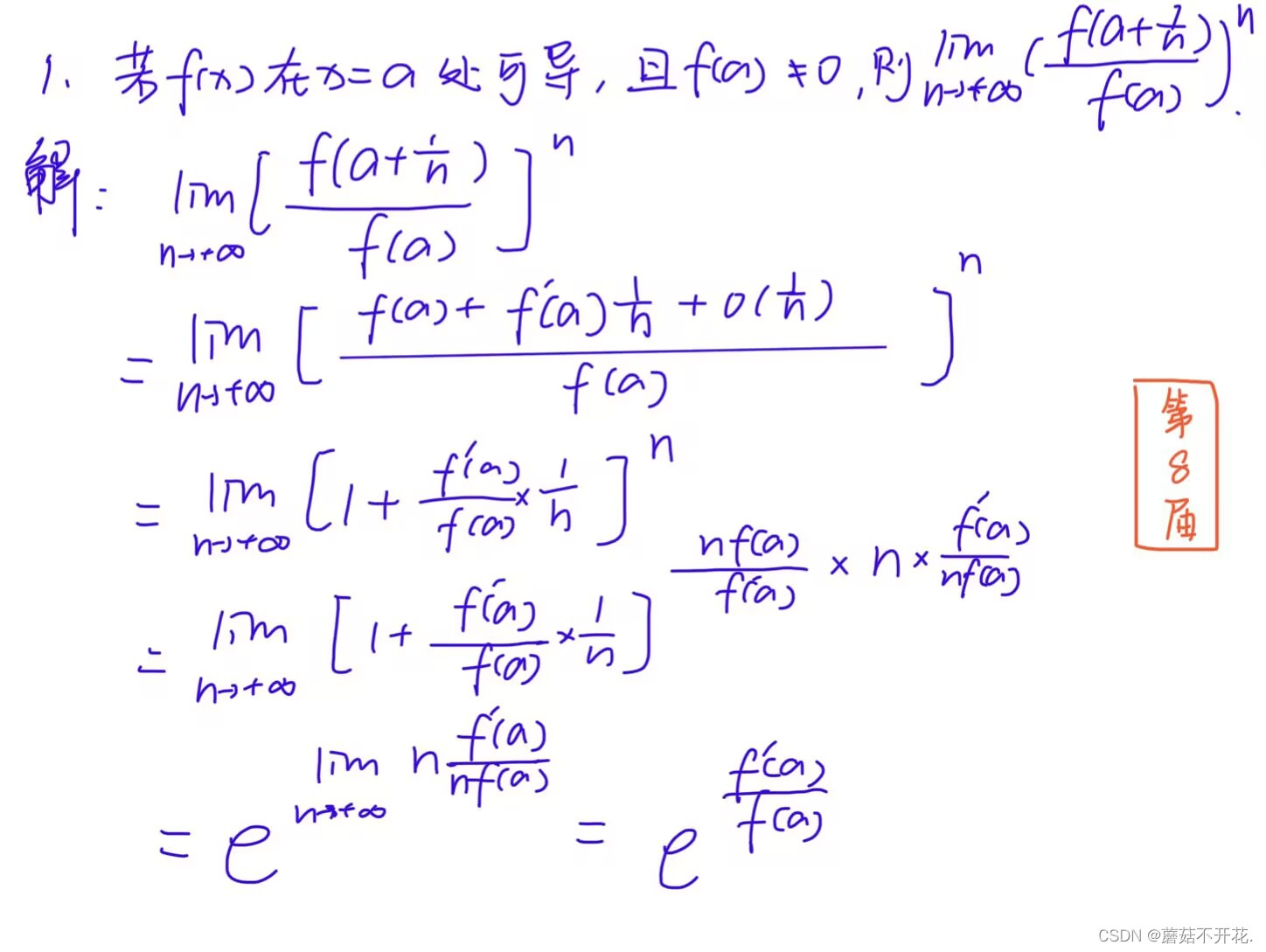
注:第一步到第二步用到了带皮亚诺余项的泰勒公式。
带皮亚诺余项的泰勒公式:
条件:f(x)在处有n阶导数;
结论:在的邻域内,有
,
其中。
在本题中,。


第7届:


注:①和②两个式子的转化用到了定积分的定义公式,推导过程如下:
 第6届:
第6届:

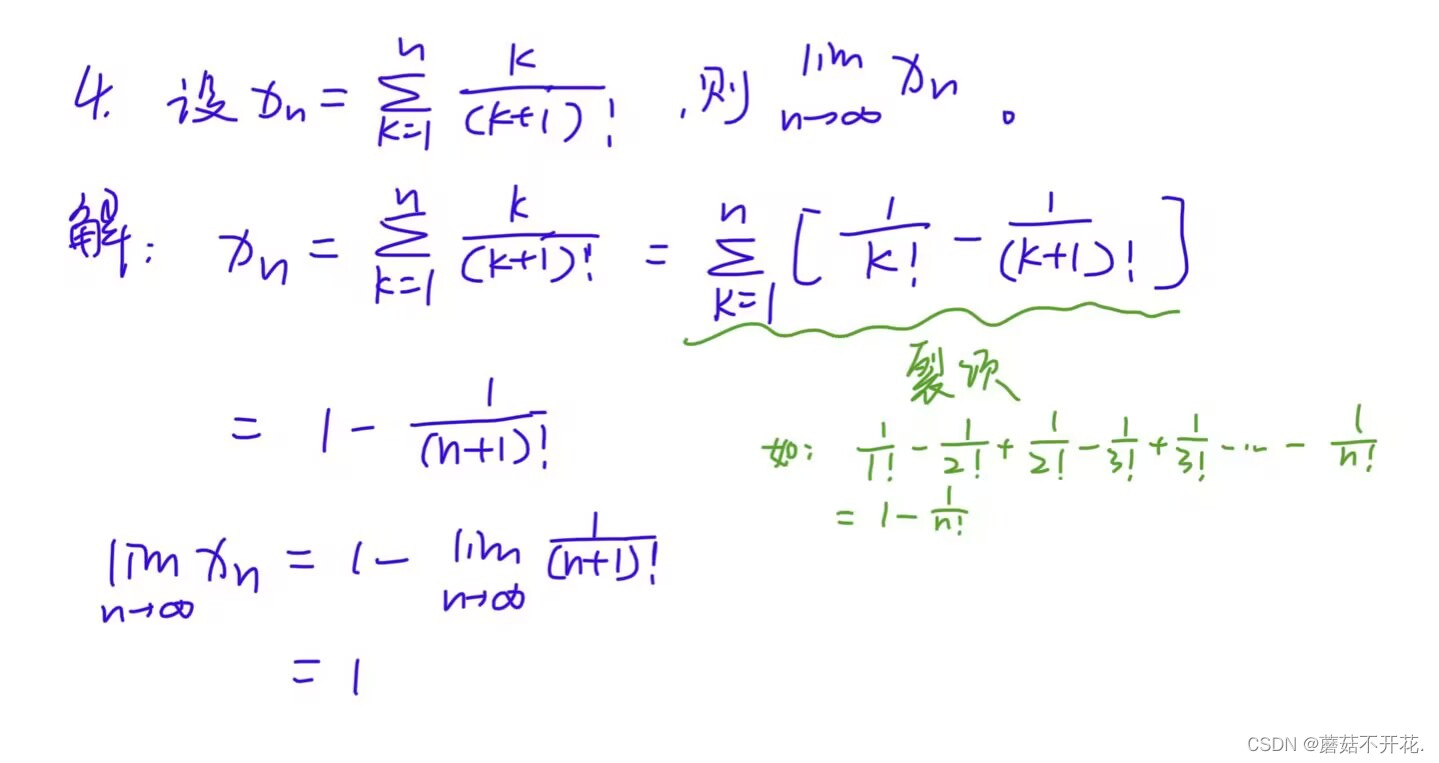


第5届:

 第4届:
第4届:
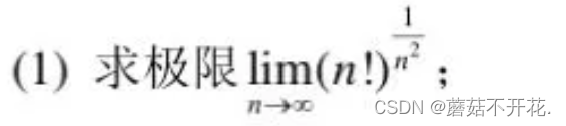
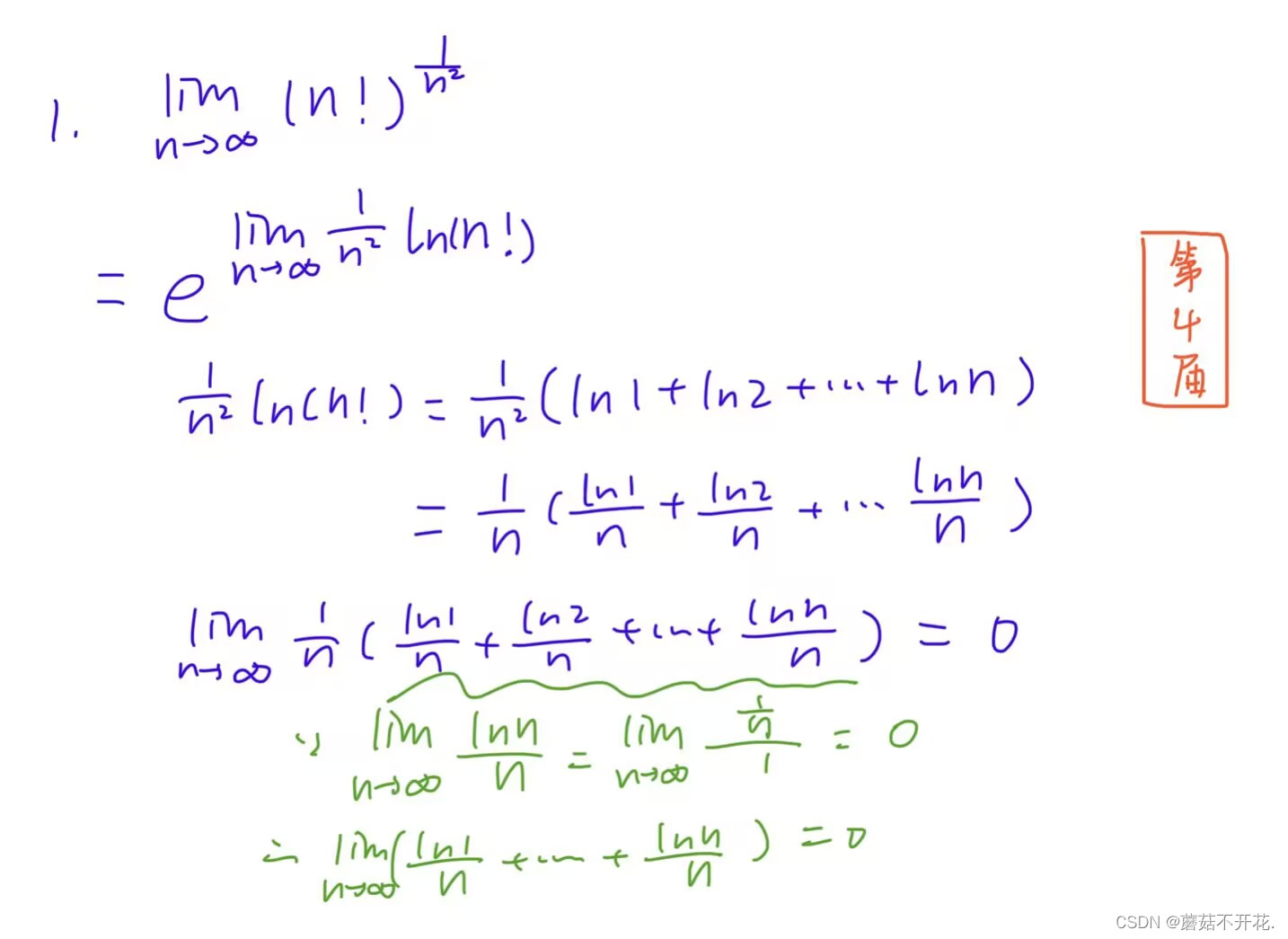
第3届:
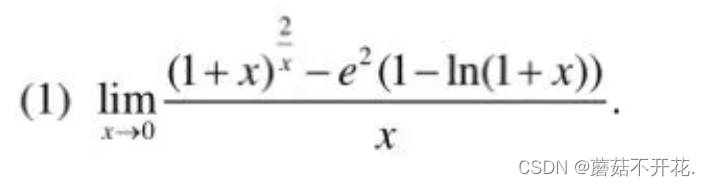

第2届:

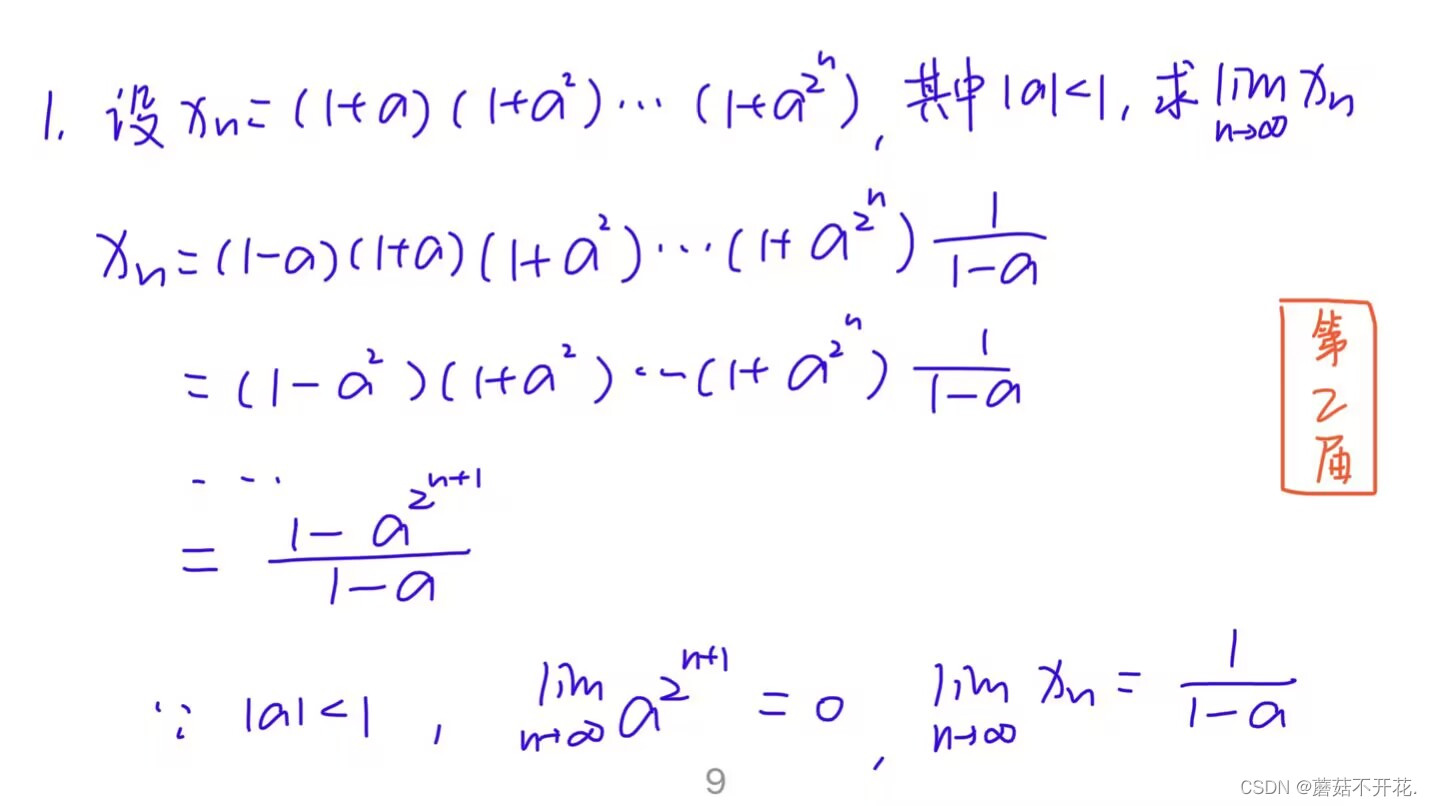

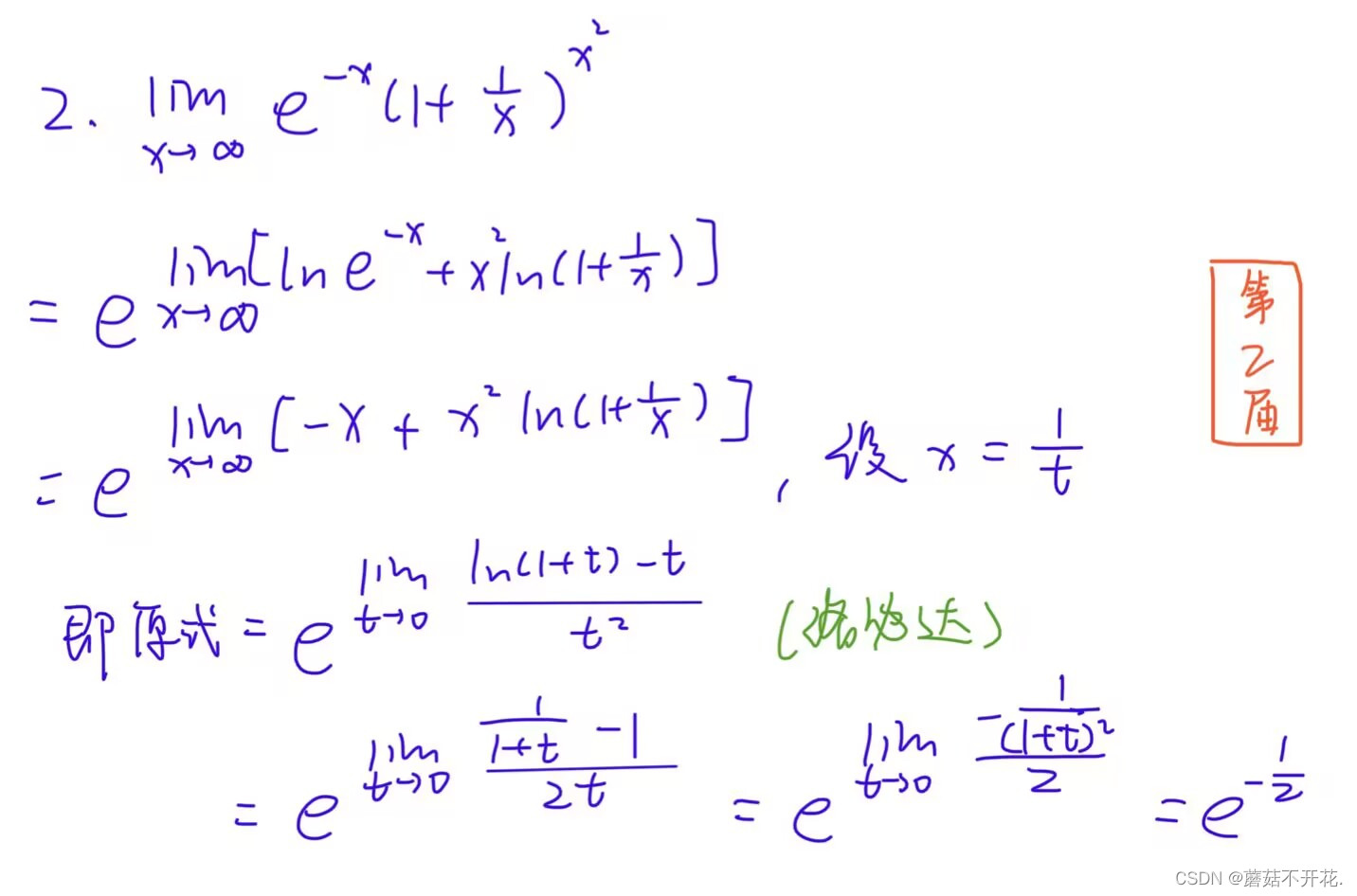
注:关于这题的其他解答方法我还尚存一些疑问,如果解决了,会在后续文章中解释~所以暂时只展示这一种方法。
第1届:


以上就是一到十四届全国大学生数学竞赛非数学类初赛的极限题了。








 文章列举了从第1届到第14届全国大学生数学竞赛非数学类初赛中的极限问题,涉及到泰勒公式(带皮亚诺余项)、定积分的运用以及无穷小的概念。每届的问题都展示了不同的数学知识点和解题技巧,部分题目解析中提到了具体的转化步骤和公式应用。
文章列举了从第1届到第14届全国大学生数学竞赛非数学类初赛中的极限问题,涉及到泰勒公式(带皮亚诺余项)、定积分的运用以及无穷小的概念。每届的问题都展示了不同的数学知识点和解题技巧,部分题目解析中提到了具体的转化步骤和公式应用。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










