树状数组 学习笔记

已于 2023-02-04 22:27:50 修改
阅读量194 收藏
点赞数 1
分类专栏： 学习笔记 文章标签： 数据结构 学习 算法
于 2022-11-05 15:31:01 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_73113801/article/details/127372001
版权

​
数据结构的本质就是对朴素算法的优化

遇到一道题目，首先先要有朴素的解题思想，将要维护的量与操作记录下来后，再考虑对应的数据结构

文章目录

P a r t 1 Part1 Part1 树状数组

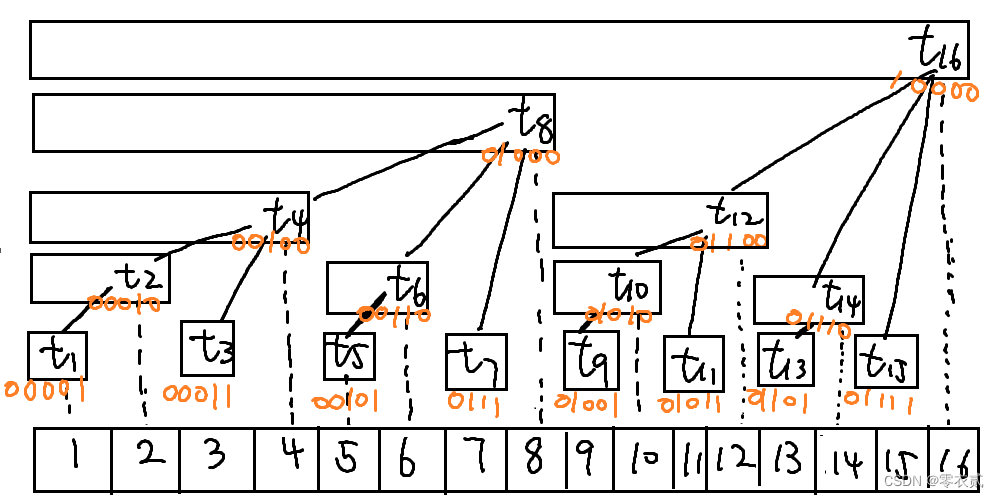
在这里插入图片描述

对于树状数组上的每一个数 x x x，可以发现， x x x 在 2 进制 {2进制} 2进制 下, 令 x x x 最后一个 1 1 1 出现的位置为 第 k k k 位， x x x 表示的区间长度即为 2 k − 1 2^{k-1} 2k−1 即 最后一个 1 1 1 的权值

例如： 14 = ( 01110 ) 2 14=(01110)_2 14=(01110)2​ 其最后一个 1 1 1 出现在第 2 2 2 位，那么 14 14 14 表示区间的长度为 2 2 − 1 = 2 2^{2-1}=2 22−1=2 即 ( 10 ) 2 (10)_2 (10)2​ 的大小
例如： 8 = ( 00100 ) 2 8=(00100)_2 8=(00100)2​ 其最后一个 1 1 1 出现在第 3 3 3 位，那么 8 8 8 表示区间的长度为 2 3 − 1 = 4 2^{3-1}=4 23−1=4 即 ( 100 ) 2 (100)_2 (100)2​ 的大小

而我们使用 l o w b i t lowbit lowbit 就可以求出该值

int lowbit(int x) 
{
	return x&(-x);
}

1 ∣ 1| 1∣ 单点修改，区间查询

  • 单点修改
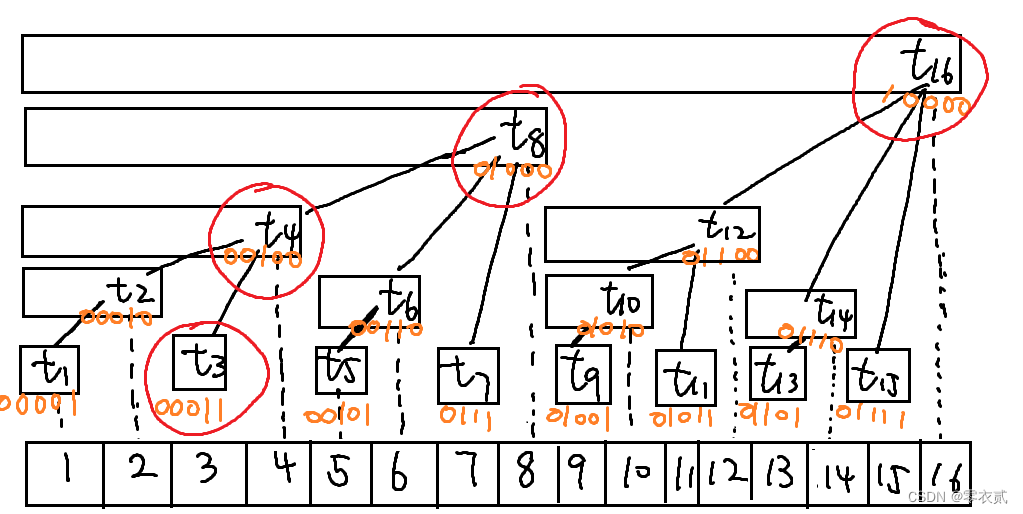
    在这里插入图片描述

以 3 3 3 为例，修改 a [ 3 ] a[3] a[3] 会对区间包含 a [ 3 ] a[3] a[3] 的点 ： t [ 3 ] , t [ 4 ] , t [ 8 ] , t [ 16 ] t[3],t[4],t[8],t[16] t[3],t[4],t[8],t[16] 造成影响

不难发现，
3 + l o w b i t ( 3 ) = 4 3+lowbit(3)=4 3+lowbit(3)=4
4 + l o w b i t ( 4 ) = 8 4+lowbit(4)=8 4+lowbit(4)=8
8 + l o w b i t ( 8 ) = 16 8+lowbit(8)=16 8+lowbit(8)=16

//单点修改
void add(int x,int delta)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree[i]+=delta;
}
  • 区间求和

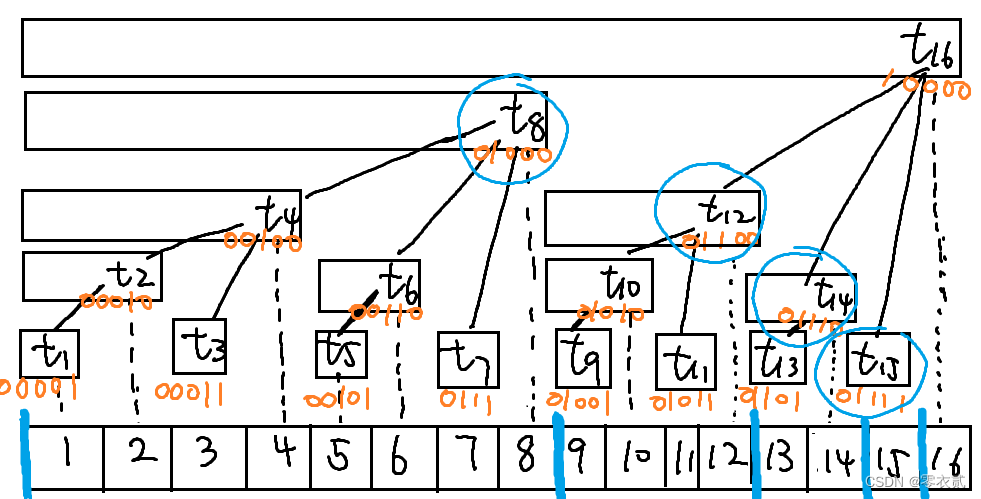
在这里插入图片描述
以 15 15 15 为例，区间 [ 1 , 15 ] [1,15] [1,15] 之和等于 t r e e [ 15 ] + t r e e [ 14 ] + t r e e [ 12 ] + t r e e [ 8 ] tree[15]+tree[14]+tree[12]+tree[8] tree[15]+tree[14]+tree[12]+tree[8] (区间 [ 15 , 15 ] [15,15] [15,15] [ 13 , 14 ] [13,14] [13,14] [ 9 , 12 ] [9,12] [9,12] [ 1 , 8 ] [1,8] [1,8] 之和)

观察可得，
15 − l o w b i t ( 15 ) = 14 15-lowbit(15)=14 15−lowbit(15)=14
14 − l o w b i t ( 14 ) = 12 14-lowbit(14)=12 14−lowbit(14)=12
12 − l o w b i t ( 12 ) = 8 12-lowbit(12)=8 12−lowbit(12)=8
8 − l o w b i t ( 8 ) = 0 8-lowbit(8)=0 8−lowbit(8)=0

就此求出区间 [ 1 , x ] [1,x] [1,x] 的和

// 区间查询 ( 区间 1 到 x 的和)
int query(int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res+=tree[i];
	return res;
}

例题：树状数组 区间求和 单点修改

  • 在每次输入时， a d d   (   i , a [ i ]   ) add\space (\space i,a[i]\space ) add ( i,a[i] )
  • 对于一个询问 [ L , R ] [L,R] [L,R] ，利用前缀和的思想，[1,R] 的和 减去 [1,L-1] 的和 即可
	cin>>n>>m;	
	for(int i=1;i<=n;i++)
		cin>>a[i], add(i,a[i]);
	while(m--)
	{
		cin>>opt;
		if(opt==1)
		{
			cin>>x>>delta;
			add(x,delta);
		}
		if(opt==2)
		{
			cin>>l>>r;
			cout<<query(r)-query(l-1)<<endl; 
		}
	}

2 ∣ 2| 2∣ 区间修改，单点查询

例题：树状数组 区间修改，单点查询

区间修改，单点查询 其实可以转换成 单点修改，区间查询

我们利用差分的思想，维护差分数组，区间 [ 1 , x ] [1,x] [1,x] 的数之和即为第 x x x 的数的值

对于区间修改 [ L , R ] [L,R] [L,R] 我们在 L L L 处加上 + d e l t a +delta +delta，在 R + 1 R+1 R+1 处加上 − d e l t a -delta −delta

	cin>>n>>m;	
	for(int i=1;i<=n;i++)
		cin>>a[i], add(i,a[i]-a[i-1]);
	while(m--)
	{
		cin>>opt;
		if(opt==1)
		{
			cin>>l>>r>>delta;
			add(l,delta);
			add(r+1,-delta);
		}
		if(opt==2)
		{
			cin>>x;
			cout<<query(x)<<endl; 
		}
	}

3 ∣ 3| 3∣ 区间修改，区间查询

例题：树状数组 区间修改，区间查询
在这里插入图片描述
t r e e 1 tree1 tree1 维护 d [ i ] d[i] d[i]
t r e e 2 tree2 tree2 维护 d [ i ] ∗ i d[i]*i d[i]∗i

对于区间 a d d add add 操作，

t r e e 1 tree1 tree1 在 L L L 处 + d e l t a +delta +delta ， 在 R + 1 R+1 R+1 处 − d e l t a -delta −delta (只影响差分数组的 L L L 与 R + 1 R+1 R+1 处)

t r e e 2 tree2 tree2 在 L L L 处 + d e l t a ∗ L +delta*L +delta∗L ， 在 R + 1 R+1 R+1 处 − d e l t a ∗ ( R + 1 ) -delta*(R+1) −delta∗(R+1)
(由于 d [ i ] d[i] d[i] 只有 L , R + 1 L,R+1 L,R+1 处改变，因此 d [ i ] ∗ i d[i]*i d[i]∗i 亦然)

对于 q u e r y query query 操作，
前缀和思想， q u e r y ( R ) − q u e r y ( L − 1 ) query(R)-query(L-1) query(R)−query(L−1)

int lowbit(int x)
{
	return x&(-x);
}
void add1(int x,int delta)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree1[i]+=delta;
}
void add2(int x,int delta)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree2[i]+=delta*x;
}
int query(int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res+=tree1[i]*(x+1)-tree2[i];
	return res;
}
signed main()
{
	cin>>n>>m;	
	for(int i=1;i<=n;i++)
		cin>>a[i], add1(i,a[i]-a[i-1]), add2(i,a[i]-a[i-1]);
	while(m--)
	{
		cin>>opt;
		if(opt==1)
		{
			cin>>l>>r>>delta;
			add1(l,delta);	add1(r+1,-delta);
			add2(l,delta);	add2(r+1,-delta);
		}
		if(opt==2)
		{
			cin>>l>>r;
			cout<<query(r)-query(l-1)<<endl;
		}
	}
	return 0;
}

4 ∣ 4| 4∣ 权值树状数组

例题：排列计数 (权值树状数组)

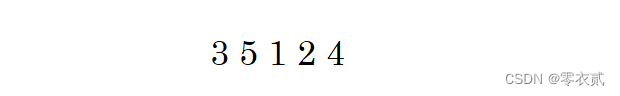
在这里插入图片描述
例如该排列，在其之前的个数为 67 67 67 ，其顺序为 68 68 68
在这里插入图片描述
则对于第 i i i 位，
令 f ( i ) f(i) f(i) 表示在 i i i 之前的未出现过的数字个数
答案 = = = ( n − i ) ! ∗ f ( i ) (n-i)!*f(i) (n−i)!∗f(i) 之和 ( i i i 从 1 1 1 到 n n n )

可以用 权值树状数组 维护 f ( i ) f(i) f(i)

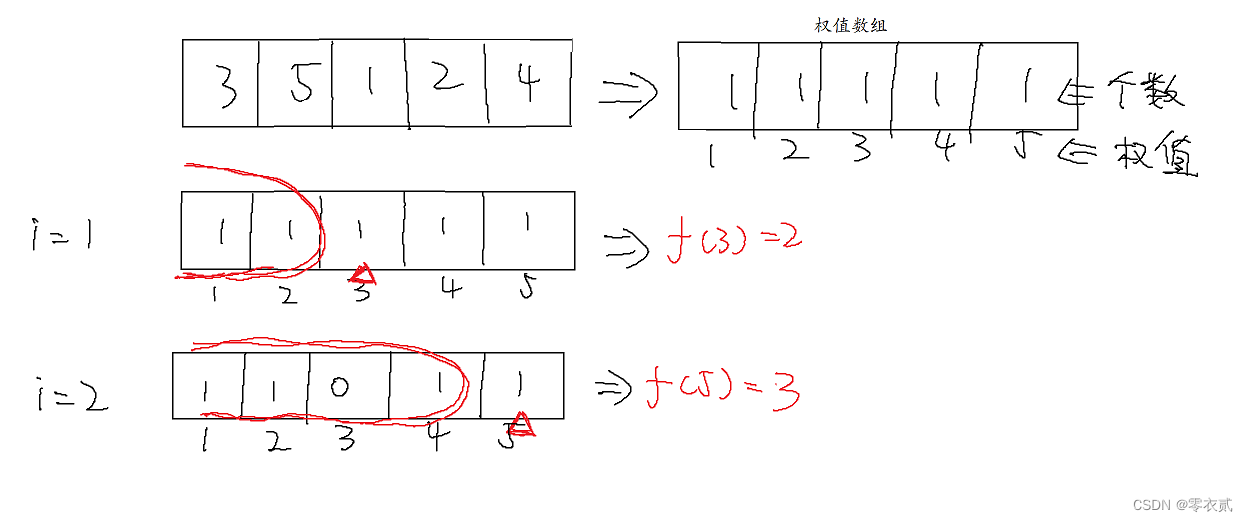
在这里插入图片描述

即化为 区间查询，单点修改

void init()
{
	calc[1]=1;
	for(int i=2;i<=n;i++)
		calc[i]=calc[i-1]*i,calc[i]%=mod;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i],add(i,1);
	init();	
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		int cnt=query(a[i]-1);
		ans+=cnt*calc[n-i], ans%=mod;
		add(a[i],-1);
	}
	cout<<ans+1;
}

5 ∣ 5| 5∣ 树状数组求第 k k k 大

由于树状数组中 t r e e [ x ] tree[x] tree[x] 管辖的区域是 l o w b i t ( x ) lowbit(x) lowbit(x) , 那么从 0 0 0 开始 , 每次加 2 i 2^i 2i , 累计的和一定表示从 1 1 1 开始的连续区间 , 根据这一特性 , 我们可以通过倍增的方式查询第一个前缀和大于等于 k k k 的某数

若我们用权值树状数组 , 那么一个数的前缀和就表示有多少数比它小

思路就是不断倍增逼近最后一个小于 k k k 的数

int select(int k)
{
	int pos = 0, cur = 0;
	for(int i=20;i>=0;i--)
	{
		pos += (1<<i);
		if(pos>n or cur+tree[pos]>=k) pos -= (1<<i);
		else cur += tree[pos];
	}
	return pos+1;
}

例题: SHOI 发牌

6 ∣ 6| 6∣ 例题

6.1 6.1 6.1 树状数组求逆序对

例题：逆序对

求逆序对及求 i < j i<j i<j 且 a i < a j a_i<a_j ai​<aj​ 的个数

用树状数组维护以 a [ i ] a[i] a[i] 为下标的权值数组

在这里插入图片描述

i i i 从小到大枚举，则在 i i i 之前已经枚举的大于 a [ i ] a[i] a[i] 的个数即为 i i i 的逆序对的个数，在枚举 i i i 之前有 i − 1 i-1 i−1 个数，因此个数 = i − 1 − q u e r y ( a [ i ] ) =i-1-query(a[i]) =i−1−query(a[i])

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=5e5+5;
int n,a[MAXN],A[MAXN],tree[MAXN];
int lowbit(int x)
{
	return x&(-x);
}
void add(int x,int delta)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree[i]+=delta;
}
int query(int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res+=tree[i];
	return res;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i], A[i]=a[i];
	sort(A+1,A+n+1);
	int cnt=unique(A+1,A+n+1)-A-1;
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(A+1,A+cnt+1,a[i])-A;
	
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		ans+=i-1-query(a[i]);
		add(a[i],1);	
	}
	cout<<ans;
	return 0;
}
6.2 6.2 6.2 树状数组去重求和

例题：去重求和

对于重复的数字，我们只关注其最后一个数字对答案的贡献

如 ： 1   2   3   2   1 1 \space 2\space 3\space 2\space 1 1 2 3 2 1
询问区间 [ 1 , 5 ] [1,5] [1,5] 不重复数字的和，等价于 0   0   3   2   1 0 \space 0\space 3\space 2\space 1 0 0 3 2 1，结果为 6 6 6

如果在该询问之后又有询问区间 [ 1 , 2 ] [1,2] [1,2] 的和，而数列已变为 0   0   3   2   1 0 \space 0\space 3\space 2\space 1 0 0 3 2 1，还需重复修改

因此我们可以建立一根扫描线，从左向右进行扫描，当某个询问的右端点与扫描线重合时，解决这次询问

至于保留最后一个数字而删除之前重复数字的操作，对于 a [ i ] a[i] a[i]，我们可以记录上一个 a [ i ] a[i] a[i] 出现的位置 l s t [ a [ i ] ] lst[a[i]] lst[a[i]]，将 l s t [ a [ i ] ] lst[a[i]] lst[a[i]] 处减去 a [ i ] a[i] a[i]

所以，此题要求单点修改，区间求和，使用树状数组

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=5e4+5;
const int MAXM=1e5+5;
int n,m,a[MAXN],ans[MAXM],tree[MAXN];
unordered_map <int,int> lst;
struct Question {
	int l,r,id;
}q[MAXM];
bool cmp(Question x,Question y) 
{
	if(x.r==y.r) return x.l<y.l;
	return x.r<y.r;
}
int lowbit(int x) {return x&(-x);}
void add(int x,int delta) 
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree[i]+=delta;
}
int query(int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res+=tree[i];
	return res;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i];
	cin>>m;
	for(int i=1;i<=m;i++)
		cin>>q[i].l>>q[i].r, q[i].id=i;
	sort(q+1,q+m+1,cmp);
	int i=1;
	for(int t=1;t<=m;t++)
	{
		for(;i<=q[t].r;i++)
		{
			if(lst[a[i]]!=0) add(lst[a[i]],-a[i]);
			lst[a[i]]=i;
			add(i,+a[i]);
		}
		ans[q[t].id]=query(q[t].r)-query(q[t].l-1);
	}
	for(int i=1;i<=m;i++) cout<<ans[i]<<endl;
	return 0;
}
6.3 6.3 6.3 权值树状数组与偏序问题

例题：铁人三项

如果存在一个运动员 j j j ，使得 x j > x i x_j>x_i xj​>xi​、 y j > y i y_j>y_i yj​>yi​、 y j > y i y_j>y_i yj​>yi​ ，则 i i i 不可用

我们先将 x x x 从大到小排序，需保证对于 j > i j>i j>i ，有 x j > x i x_j >x_i xj​>xi​ 这样只要存在 j j j 的 y j > y i , z j > z i y_j>y_i,z_j>z_i yj​>yi​,zj​>zi​,也就是说只要之前出现过 y j > y i , z j > z i y_j>y_i,z_j>z_i yj​>yi​,zj​>zi​ ， i i i 就不可用

那么在所有满足 y j > y i y_j>y_i yj​>yi​ 的 j j j 中 ，只要 m a x max max{ z j z_j zj​} > z i >z_i >zi​ ， i i i 就不可用

用权值树状数组维护一个以 y y y 的值为下标，以 z m a x z_{max} zmax​ 为值的数组

树状数组可维护前缀最大值，我们现在要求的是 y j > y i y_j>y_i yj​>yi​ 的, 因此我们需要通过处理将 y y y 按倒序存储

例：
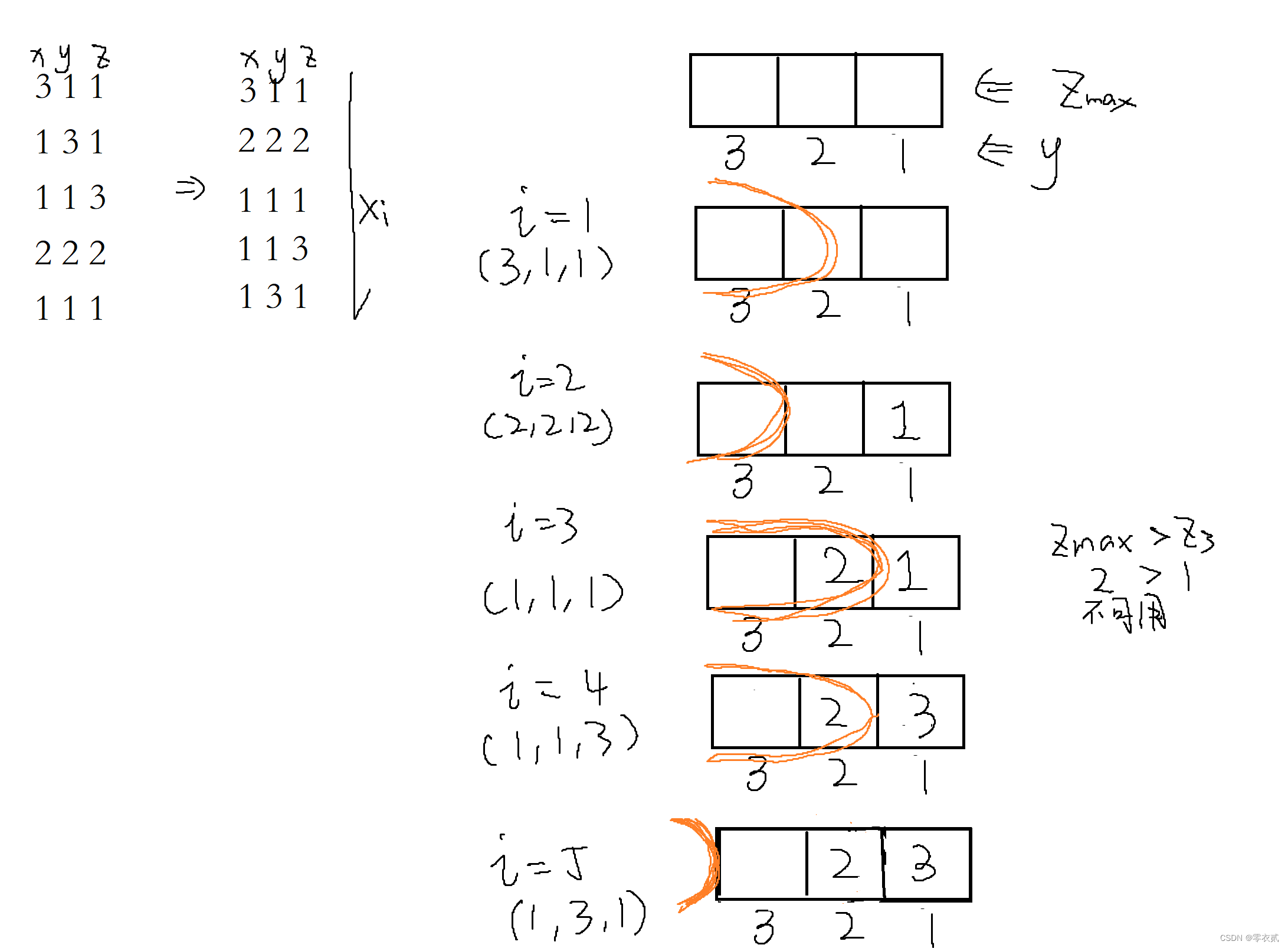
在这里插入图片描述

  • 注意的细节
    • 1 ∣ 1| 1∣ 记 y i ′ = n − y i + 1 y_i'=n-y_i+1 yi′​=n−yi​+1 ，即可实现将 y y y 倒序处理，加 1 1 1 是为了防止 y ′ = 0 y'=0 y′=0 导致树状数组卡死
    • 2 ∣ 2| 2∣ 对于每个 i i i ，需要询问 < y i <y_i <yi​ 的 最大 z z z ，因此应该先访问 y i y_i yi​ 比较小的，再访问 y i y_i yi​ 较大的

#include<bits/stdc++.h>
using namespace std;
const int MAXN=1e5+5;
struct Node{
	int x,y,z;
}a[MAXN];
int n,tree[MAXN];
bool cmp(Node t1,Node t2)
{
	if(t1.x==t2.x) return t1.y<t2.y;// 细节2
	return t1.x>t2.x;
}
bool bad[MAXN];
int lowbit(int x) 
{
	return x&(-x);
}
void add(int x,int val)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree[i]=max(tree[i],val);
}
int query(int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res=max(tree[i],res);
	return res;
} 
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i].x>>a[i].y>>a[i].z;
	sort(a+1,a+n+1,cmp);
	int cnt=n;
	for(int i=1;i<=n;i++)
	{
		if(query(n-a[i].y)>a[i].z)//细节1
			cnt--;
		add(n-a[i].y+1,a[i].z);//细节1
	}
	cout<<cnt;
	return 0;
}
6.4 6.4 6.4 权值树状数组优化dp

例题：Cow Protests

d p dp dp 转移方程： s u m sum sum 表示前缀和
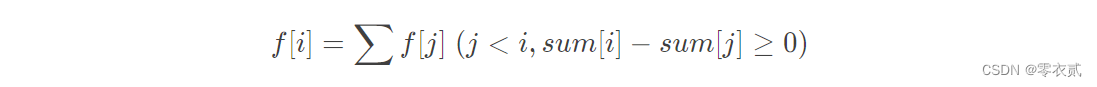
在这里插入图片描述

	f[0]=1;
	for(int i=1;i<=n;i++)
		for(int j=0;j<i;j++)
		{
			if(sum[i]<0 || sum[j]<0) continue;
			if(sum[i]-sum[j]>=0)
			{
				f[i]+=f[j],	f[i]%=mod;
			} 
		}

看到这题就觉得和 usaco 的 Bookshelf 和 TJOI 的书架 很像，只不过那两题是求 f [ j ] f[j] f[j] 的最大值，详见 线段树优化dp，此题变为了求 f [ j ] f[j] f[j] 的和，可以考虑使用树状数组

  • 具体实现：
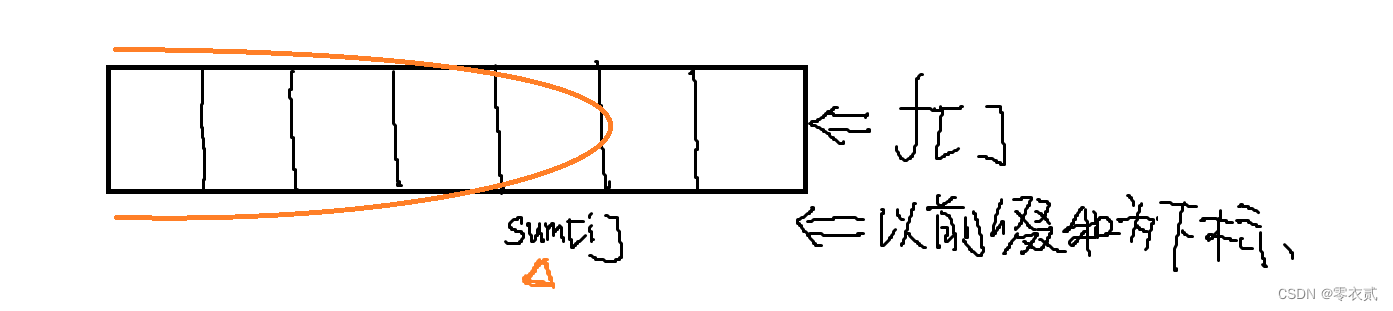
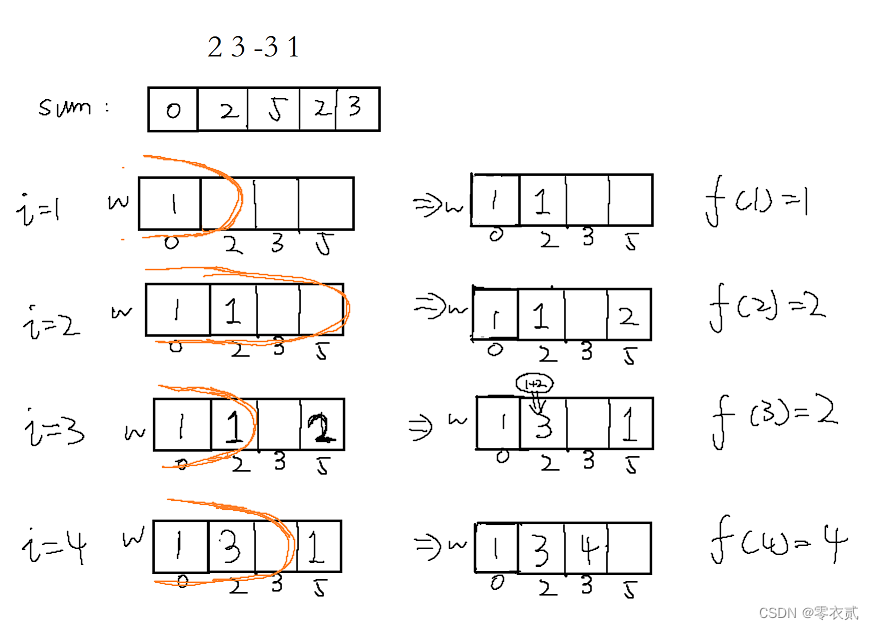
    在这里插入图片描述

在这里插入图片描述

i i i 从小到大开始枚举，则在 i i i 之前已枚举的数 并且 满足 s u m ≤ s u m [ i ] sum \leq sum[i] sum≤sum[i] 的 f f f 之和 ，即图中小于等于 s u m [ i ] sum[i] sum[i] 的 f f f 总和，即为 f [ i ] f[i] f[i] 的值

以前缀和为下标，用权值树状数组维护

此题由于可能为负数，我们需要离散化处理

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=1e5+5;
const int mod=1e9+9;
int n,a[MAXN],x[MAXN],sum[MAXN],pos[MAXN],f[MAXN],tree[MAXN]; 
int lowbit(int x)
{
	return x&(-x);
}
void add(int x,int delta)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree[i]+=delta, tree[i]%=mod;
}
int query(int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res+=tree[i], tree[i]%=mod;
	return res;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i], sum[i]=sum[i-1]+a[i], x[i]=sum[i], x[i]=sum[i]%=mod;
	
	sort(x+1,x+n+1);
	int cnt=unique(x+1,x+n+1)-x-1;
	for(int i=1;i<=n;i++)
		pos[i]=lower_bound(x+1,x+cnt+1,sum[i])-x;	
	
	pos[0]=lower_bound(x+1,x+cnt+1,0)-x;	
	
	add(pos[0],1);
	for(int i=1;i<=n;i++)
	{
		f[i]=query(pos[i]), f[i]%=mod;
		add(pos[i],f[i]);
	}
	cout<<f[n];
	return 0;
}
6.5 6.5 6.5 树状数组求顺序数对

例题：132型数对

直接从132型数对不好求，而我们可以很容易将 123 型和 132 型一起求出

记所有 j < i j<i j<i 且 a [ j ] < a [ i ] a[j]<a[i] a[j]<a[i] 的 j j j 的个数为 L [ i ] L[i] L[i]
记所有 i < j i<j i<j 且 a [ i ] < a [ j ] a[i]<a[j] a[i]<a[j] 的 j j j 的个数为 R [ i ] R[i] R[i]

对于求 132+123 型数对 ，枚举 i i i 作为左端点， R [ i ] ∗ ( R [ i ] − 1 ) / 2 R[i]*(R[i]-1)/2 R[i]∗(R[i]−1)/2 即为以 i i i 为左端点的该数对个数

对于 123 型个数，枚举 i i i 作为中间点， L [ i ] ∗ R [ i ] L[i]*R[i] L[i]∗R[i] 即为以 i i i 为中间点的该数对个数

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MAXN=2e4+5;
int n,a[MAXN],A[MAXN],tree1[MAXN],tree2[MAXN],L[MAXN],R[MAXN],tot1,tot2;
int lowbit(int x)
{
	return x&(-x);
}
void add(int *tree,int x,int delta)
{
	for(int i=x;i<=n;i+=lowbit(i))
		tree[i]+=delta;
}
int query(int *tree,int x)
{
	int res=0;
	for(int i=x;i>0;i-=lowbit(i))
		res+=tree[i];
	return res;
}
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>a[i], A[i]=a[i];
	sort(A+1,A+1+n);
	int cnt=unique(A+1,A+1+n)-A-1;
	for(int i=1;i<=n;i++)
		a[i]=lower_bound(A+1,A+cnt+1,a[i])-A;
	
	for(int i=1;i<=n;i++)
	{
		L[i]=query(tree1,a[i]-1);
		add(tree1,a[i],+1);
	}
	for(int i=n;i>=1;i--)
	{
		R[i]=query(tree2,n-a[i]);
		add(tree2,n-a[i]+1,+1);;
	}
	for(int i=1;i<=n;i++)
	{
		tot1+=R[i]*(R[i]-1)/2; 
		tot2+=L[i]*R[i];
	}
	cout<<tot1-tot2;
	return 0;
}
零衣贰
关注
  • 1
    点赞
  • 踩
  • 0
    收藏
    觉得还不错? 一键收藏
  • 1
    评论
专栏目录
树状数组学习笔记
m0_72545392的博客
09-24 164
树状数组学习及hh的项链题目详解
树状数组学习笔记(Python)
m0_72379992的博客
04-02 826
拜读了大佬的讲解博文，写一篇Python版的笔记巩固消化，附带蓝桥杯历年真题作为例题演示。
AcWing树状数组学习笔记 附二分查找基本知识
qq_49620160的博客
11-03 372
目录 什么是树状数组？ 基本操作： 拓展操作： 树状数组的相关题目 （1）AcWing楼兰图腾241： （2）AcWing 一个简单的整数问题245、264 关于二分 实数域上的二分： 什么是树状数组？ 对于树状数组 tr[u] 区间，将u进行二进制拆分，可以得到的最低位的1的位数，即为tr[u] 的“管辖范围”。一个 tr[u] 存储了一定区间内所有的元素的和，这个区间的长度由该区间末位的二进制最低位的1的位数（即 lowbit（x）= ...
RMQ | ST 表 | 树状数组 学习笔记
TMJYH09's csdn blog
02-16 297
前言 前段时间没啥空写博客，今天汇总一下这几天学的几种数据结构。 Part1. ST 表 ST 表是用于求解 RMQ（区间最值） 问题的一种数据结构，使用了倍增的思想，时间复杂度 O(nlog⁡n)\mathcal{O}(n\log n)O(nlogn)。 本人认为 ST 表很类似区间 dp。 有一个数组 aaa，假设现在要求静态区间最大值。 I. 创建 ST 表 首先定义 ST 表 sti,jst_{i,j}sti,j​ 表示 [i,i+2j−1][i,i+2^j-1][i,i+2j−1] 这段区间的最大
树状数组Web-maste开发笔记
06-10
树状数组，也被称为二叉索引树（Binary Indexed Tree, BIT）或 Fenwick 树，是一种高效的数据结构，常用于解决与数组相关的在线查询和更新问题。在Java编程中，树状数组能够帮助我们快速地实现前缀和查询、区间修改...
树状数组vaWeb-m开发笔记
06-11
【树状数组vaWeb-m开发笔记】是一份深入探讨JavaWeb开发中树状数组应用的文档，主要针对Java程序员提供关于高效数据结构和算法在实际项目中的应用指导。树状数组，又称线段树（Segment Tree），是计算机科学中一种...
树状数组Web-master- 开发笔记
06-11
树状数组，也被称为二进制索引树（Binary Indexed Tree, BIT），是计算机科学中一种数据结构，常用于高效地处理数组上的区间查询和更新操作。在Java编程语言中，树状数组是一种非常有用的工具，尤其在算法竞赛和数据...
树状数组-2023C-m开发笔记
06-09
树状数组，也被称为线段树（Segment Tree），是一种数据结构，主要应用于处理区间查询与更新问题。在C语言中实现树状数组，可以高效地处理动态维护区间和单点修改的问题，通常具有O(logn)的时间复杂度。这篇2023C-m...
JS基本功DOM学习笔记
07-12
1. **DOM树**：DOM将网页内容表示为一棵由节点构成的树形结构，其中每个节点代表HTML元素、属性、文本等。根节点通常是`document`，其他节点如`<div>`、`<p>`等是元素节点，而文本和注释则是文本节点。 2. **DOM...
数据结构--二叉树和堆
binhyun的博客
07-07 822
1.基本概念 2.树的遍历方法 3.满二叉树&&完全二叉树 4.逻辑结构&&物理结构 5.推理公式 6.二叉树应用--堆 7.简单实现堆
[数据结构] 基于插入的排序 插入排序&希尔排序
水墨不写bug
07-06 1140
插入排序&&希尔排序 实现原理
D1.排序
2302_79232710的博客
07-07 176
快速排序和归并排序
数据结构之顺序表
m0_73634434的博客
07-10 301
线性表(List)由零个或多个数据组成的有限数列，线性表是一种在实际中广泛使用的数据结构，常见的线性表：顺序表，链表，栈，队列，字符串。
【排序 - 堆排序】
最新发布
2302_80393814的博客
07-10 256
堆排序利用堆这种数据结构的特性，通过构建最大堆和不断调整堆的过程来实现排序。它的时间复杂度稳定在 O(n log n)，并且适用于大数据量的排序需求。通过本文，我们深入了解了堆排序的原理和实现方式，并通过C语言代码展示了如何实现堆排序算法。对于理解高效排序算法和算法设计有着重要的帮助。
数据结构--单链表实现
LH__1314的博客
07-05 1380
链表和顺序表都是线性表的一种，但是顺序表在物理结构和逻辑结构上都是连续的，但链表在逻辑结构上是连续的，而在物理结构上不一定连续；来看以下图片来认识链表与顺序表的差别这里以动态顺序表为例，和链表中的单链表对比一下动态顺序表单链表这里就可以很清晰的看到顺序表的底层其实就是一个数组，数据的是连续存储的（顺序表物理结构连续）；而链表它每一个数据都不是连续的（链表物理结构上不一定连续）。链表节点通过观察上图，我们会发现链表每一个节点都存放在数据和下一个节点的地址。
代码随想录第十二天|226.翻转二叉树、 101.对称二叉树、104.二叉树的最大深度、111.二叉树的最小深度
semirc9的博客
07-09 629
二叉树
【力扣】每日一题—第217题，存在重复元素
m0_65146517的博客
07-05 325
暴力求解两重for循环直接出结果，但是超时了！如果数组中每个元素互不相同，返回。如果任一值在数组中出现。感觉自己越来越厉害了，哎，不过如此，嘿嘿嘿。
【算法】排序算法介绍 附带C#和Python实现代码
Xiaoxin的博客
07-10 1107
排序算法是计算机科学中的一个基础而重要的部分，用于将一组数据按照一定的顺序排列。下面介绍几种常见的排序算法，并分别用C#和Python给出实现代码。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值