【算法】线段树

最新推荐文章于 2024-07-15 22:10:26 发布

风雪心

最新推荐文章于 2024-07-15 22:10:26 发布

阅读量1.2k

点赞数 23

分类专栏：算法和数据结构文章标签：算法数据结构后端

本文链接：https://blog.csdn.net/weixin_73366312/article/details/137600768

版权

算法和数据结构专栏收录该内容

15 篇文章 0 订阅

订阅专栏

线段树（Segment Tree）几乎是算法竞赛最常用的数据结构了，它主要用于维护区间信息（要求满足结合律）。与树状数组相比，它可以实现 $O(\log n)$ 的区间修改，还可以同时支持多种操作（加、乘），更具通用性。

洛谷 P3372【模板】线段树1

【模板】线段树 1 - 洛谷

题目描述
如题，已知一个数列，你需要进行下面两种操作：
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入格式
第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数，表示一个操作，具体如下：
操作1：格式：1 x y k 含义：将区间[x,y]内每个数加上k
操作2：格式：2 x y 含义：输出区间[x,y]内每个数的和
输出格式
输出包含若干行整数，即为所有操作2的结果。

一、线段树的性质：

线段树是一棵平衡二叉树。母结点代表整个区间的和，越往下区间越小。注意，线段树的每个节点都对应一条线段（区间），但并不保证所有的线段（区间）都是线段树的节点，这两者应当区分开。

如果有一个数组[1,2,3,4,5]，那么它对应的线段树大概长这个样子：

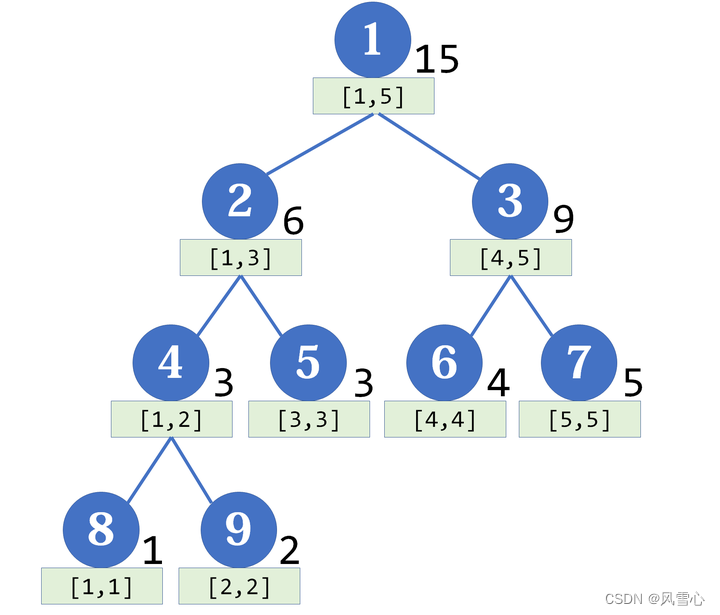
每个节点 $p$ 的左右子节点的编号分别是 $2p$ 和 $2p+1$ ，假如节点 $p$ 存储区间 $[a,b]$ 的和，设 $mid=\left \lfloor \frac{l+r}{2} \right \rfloor$ ,那么两个子节点分别存储 $[l,mid]$ 和 $[mid+1,r]$ 的和。可以发现，左节点对应的区间长度，与右节点相同或与之相比恰好多1。

二、线段树的常用结论

（1）如果一棵线段树有N个叶子节点，则其必定有N-1个非叶子节点，总节点个数为2N-1个。本结论详细证明请见线段树数组的开辟大小的结论证明部分。

（2）一棵线段树中的节点，其度数仅能为0或2，不存在度数为1的节点。

线段树的所有叶子结点的区间都仅包含一个下标元素，且单个的叶子节点不能再进一步被拆分。线段树的非叶子节点的对应区间的上下限必定不同，且可以被进一步拆分成更小的节点元素。因此线段树中叶子节点的度数为0，非叶子节点的度数为2。

（3）线段树不一定是完全二叉树

线段树不一定是完全二叉树，主要基于以下几个原因：

1.区间长度不一：线段树是用来处理区间问题的数据结构，而这些区间的长度可能并不相等。当我们将一个大的区间划分为两个子区间时，这两个子区间的长度可能是不同的。这种不均匀的划分会导致线段树的某些节点只有左子节点或只有右子节点，因此不满足完全二叉树的每个节点都有两个子节点的要求。

2.空间优化：在实际应用中，为了节省空间，我们可能会采用一些优化手段，例如懒惰标记（Lazy Propagation）或者动态分配节点。这些优化可能会导致线段树在某些情况下并不是满二叉树，即不是每个节点都有两个子节点。

3.特殊操作：在某些情况下，我们可能需要对线段树进行特殊操作，如合并两个线段树或从一个线段树中删除一部分区间。这些操作可能会破坏线段树原本的结构，使其不再是一个完全二叉树。

4.实现方式：线段树的实现方式并不是唯一的。虽然标准的线段树实现通常是基于递归的二分划分，但也可以有其他实现方式。这些不同的实现方式可能会导致线段树的结构有所不同，包括不一定是完全二叉树。

特殊地，一棵线段树可以仅存在单独的左子节点或者右子节点。

举个例子，假设我们有一个线段树用来处理一个包含5个元素的数组[a, b, c, d, e]。如果我们选择以第一个元素a为根节点代表的区间，并试图以某个方式将其划分为两个子区间，那么可能会出现只有左子节点或只有右子节点的情况。

1.只有左子节点：如果我们决定只将a作为根节点的左子节点代表的区间，而不对剩余的元素[b, c, d, e]进行进一步的划分，那么根节点的右子节点将是空的。这通常不是一个实用的选择，因为线段树的目的是为了高效地处理区间查询和更新，而只包含一个元素的左子节点并没有充分利用线段树的结构优势。

2.只有右子节点：一个更实际的例子是，如果我们首先以整个数组[a, b, c, d, e]作为根节点的区间，并决定首先划分掉右半部分[c, d, e]作为右子节点代表的区间。然后，如果我们选择不再对左半部分[a, b]进行划分，那么左子节点将是空的，而右子节点将包含三个元素的区间。这种情况在实际应用中可能发生，特别是当我们根据具体需求对线段树进行定制或优化时。

综上所述，线段树的结构是根据处理区间的需求来构建的，其目的主要是为了高效地处理区间查询和更新操作。虽然线段树在某些情况下可能呈现出类似于完全二叉树的结构，但由于上述原因，它并不一定是完全二叉树。

那么线段树需要满足什么条件，可以将它视为完全二叉树呢？有以下几个条件：

1.区间均匀划分：当处理的区间长度始终为2的幂次方，并且在构建线段树时，每个区间都被均匀地划分为两个等长的子区间时，线段树将呈现为完全二叉树。这是因为每次划分都保持二分性，每个节点都有两个子节点，除非它是叶子节点（代表单个元素的区间）。

2.没有优化或特殊操作：如果在线段树的构建和使用过程中，没有采用任何空间优化手段（如懒惰标记）或特殊操作（如合并或删除部分区间），线段树将保持其原始的、基于递归二分划分的结构，从而呈现出完全二叉树的形式。

3.静态线段树：在处理静态数据集（即数据不会改变）时，通常可以构建出完全二叉树的线段树结构。因为对于静态线段树，一旦构建完成，就不需要再对其结构进行修改，所以它可以保持为一个标准的完全二叉树。

（4）线段树所表示的区间长度等同于所有叶节点的数量之和

由于线段树所表示的总区间最后都将拆分为单独的叶子节点，而每个叶子节点表示一个独立的元素，因此，线段树表示的区间长度等同于所有叶节点的数量之和。

（5）线段树表示的不一定是一段连续的区间

虽然线段树最常见的应用是处理连续的区间查询和更新问题，但其数据结构本身并不局限于表示连续区间。线段树是一种二叉树结构，其每个节点代表一个区间，并通过递归地将区间划分为更小的子区间来构建整棵树。因此，只要能够将问题抽象为区间形式，无论是连续的还是非连续的，都有可能使用线段树来解决。

在实际应用中，有些问题可能涉及非连续的区间或者具有特殊区间结构的数据。在这些情况下，可以通过自定义线段树的节点和区间表示方式，以适应非连续区间的处理。例如，可以将线段树的节点设计为包含多个不连续的子区间，或者根据问题的需求对区间进行特殊的合并和划分操作。

（6）均匀划分的线段树的左子树和右子树区间长度之差总是小于等于1，即叶节点个数之差总是小于等于1。需要强调的是这里的线段树必须是均匀划分的，如果人为地将一个区间划分成不均匀的形式，则该结论将不再成立。

（7）线段树是平衡二叉树

三、线段树的建立

1.线段树数组的开辟

如果区间长度为N，则需要开辟一个长度为4*N的一维数组来实现对线段树所有节点的存储。

ll tree[MAXN*4];//开辟一个四倍大小的一维数组用来存储线段树的所有节点

原因：

线段树的节点的数组需要开辟原大小的四倍空间主要与其构建方式和更新操作有关。

线段树是一种二叉树结构，用于高效地解决一些与区间查询和更新有关的问题。在构建线段树时，对于每个区间，我们都会创建一个对应的节点来存储该区间的信息。由于线段树是完全二叉树，所以其空间复杂度为O(n)，其中n为原始数据的个数。

然而，当我们考虑更新操作时，情况会发生变化。在更新线段树中的一个节点时，我们可能需要递归地更新该节点的所有祖先节点，以确保线段树的正确性。在最坏的情况下，当我们更新线段树的根节点时，我们可能需要更新所有的节点。因此，为了确保在更新过程中有足够的空间来存储所有的节点，我们通常需要为线段树分配更多的空间。

具体来说，对于包含n个元素的数组，其对应的线段树有n个叶子节点（每个叶子节点对应数组中的一个元素），以及n-1个非叶子节点（用于合并子区间的信息）。因此，总共有2n-1个节点。而在线段树的运算中，第2n-1个节点的子节点的最大下标可达到2*(2n-1)+1=4n-1个。因此，为了确保能够存储所有的节点，我们通常将线段树数组的大小设置为4n，这样即使在最坏的情况下也能有足够的空间来存储所有的节点。

对于“结论：如果一棵线段树有n个叶子节点，则其必定有n-1个非叶子节点，总共有2n-1个节点。”的推导证明：

证法一：栽树原理

由线段树的性质可知，线段树的所有叶子结点的区间都仅包含一个下标元素，且单个的叶子节点不能再进一步被拆分。线段树的非叶子节点的对应区间的上下限必定不同，且可以被进一步拆分成更小的节点元素。由于整个区间包含n个元素，每个元素最后都成为一个单独的叶子节点，因此有n个叶子节点。

对这n个叶子结点按照数值从小到大进行排序。然后开始通过叶子节点合成非叶子节点。根据非叶子节点的定义可知，至少需要两个叶子节点才能合成一个非叶子节点。以下仅以上面列举的[1,2,3,4,5]的区间进行证明，该结论可进一步推广到一般情况。

首先由[1,1]和[2,2]可合成第一个非叶子节点①[1,2]，在该过程中，生成区间为[1,2]（即可认为1和2之间建立了连接）。然后我们以这个非叶子节点为基础，将它与叶子节点[3,3]合并，生成了第二个非叶子节点②[1,3]，在这一过程中，生成区间为[2,3]。同理可得③的生成区间为[3,4]，④的生成区间为[4,5]。由栽树原理可知，如果有n个叶子节点，则有n-1个生成区间，每一个生成区间都将对应一个非叶子节点，因此，一棵有n个叶子节点的线段树必定有n-1个非叶子节点，总共有2n-1个节点。

注意：本证明之所以能采用栽树原理，主要在于对线段树的划分，每次都将一个非叶子节点划分为两个子节点，因此可以认为非叶子节点的数量与它划分出的子节点的数量满足栽树原理中间隔和树的关系。如果对一个非叶子节点进行两个以上的子节点的划分，则栽树原理将不再适用。

证法二：完全二叉树的性质

由线段树的性质可知，线段树的所有叶子结点的区间都仅包含一个下标元素，且单个的叶子节点不能再进一步被拆分。线段树的非叶子节点的对应区间的上下限必定不同，且可以被进一步拆分成更小的节点元素。而每个叶子节点的度数为0，由于每个非叶子节点都可被拆分成两个更小的子节点，因此非叶子节点的度数为2。即可知，线段树中一个节点的度数要么为0，要么为2，不存在度数为1的节点。

又由于静态的线段树是完全二叉树，因此根据完全二叉树的节点性质可知， $n_{0}=n_{2}+1$ , $n_{0}=n$ ,进而得出 $n_{2}=n-1$ ,所以非叶子节点个数必定为n-1个，结论得证。

证法三：等比数列

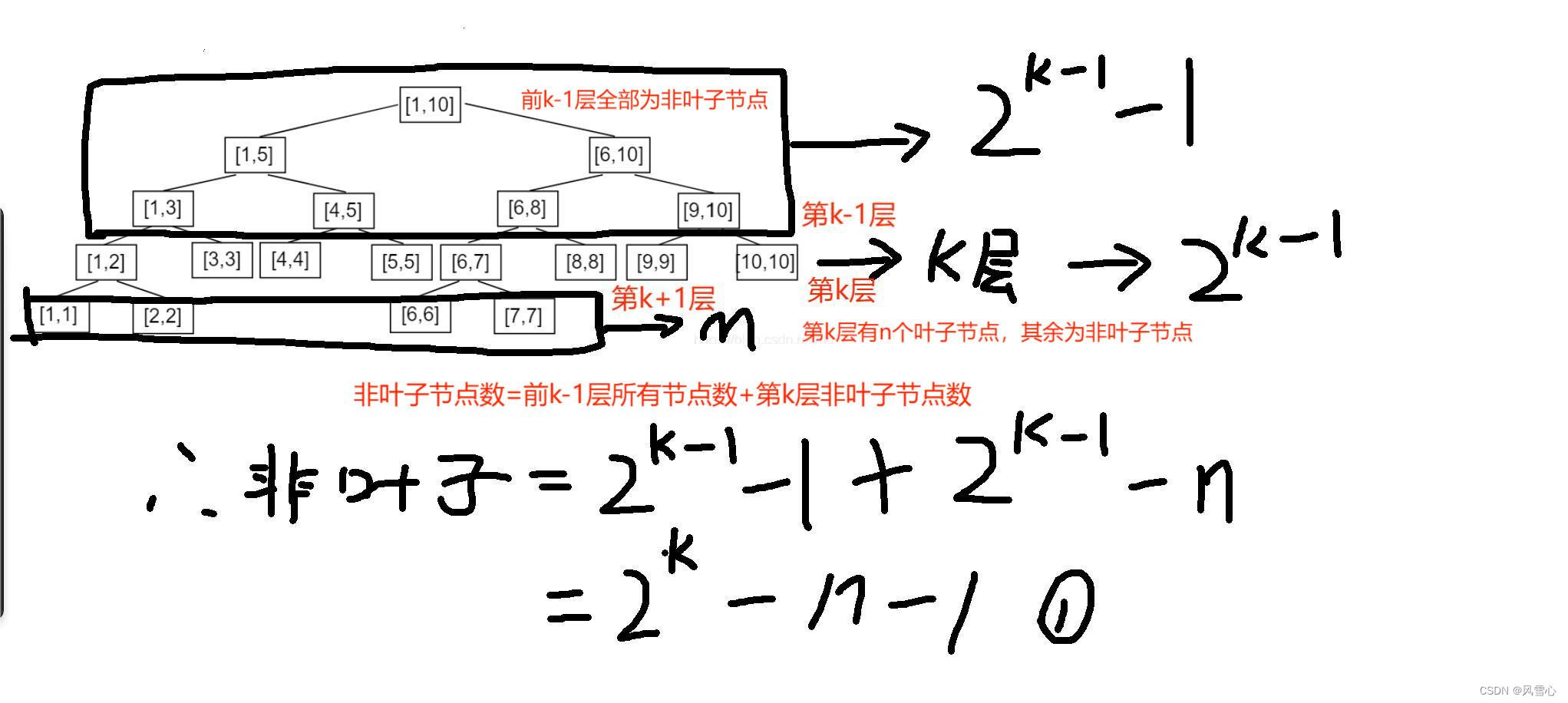
由于线段树是一棵完全二叉树，而根据完全二叉树和满二叉树的性质可知，如果一棵满二叉树总共有k层，则总节点数为 $2^{k}-1$ ，对于任意的 $i\in [1,k]$ ，均满足 $n_{i}=2^{i-1}$ ,所以第k层的节点个数 $n_{k}=2^{k-1}$ ,在总结点数和第k层节点数之间建立联系，有： $n_{all}=2n_{k}-1$ 。假设线段树包含的区间为N，最后一层叶子节点个数为m，倒数第二层个数为n，则有m+n=N。

2.线段树建立的代码实现

可以以数组为基础递归地建立一棵线段树。

void build(ll l = 1, ll r = n, ll p = 1)
{
    if (l == r) // 到达叶子节点
        tree[p] = A[l]; // 用数组中的数据赋值
    else       //如果这个节点不是叶子节点
    {
        ll mid = (l + r) / 2;   //对节点所对应的区间进行一个左右区间划分
        build(l, mid, p * 2); // 先建立左右子节点
        build(mid + 1, r, p * 2 + 1);
        tree[p] = tree[p * 2] + tree[p * 2 + 1]; // 该节点的值等于左右子节点之和
    }
}

Gif展现动态过程：

四、线段树的区间修改

在讲区间修改前，要先引入一个“懒标记”（或延迟标记）的概念。懒标记是线段树的精髓所在。对于区间修改，朴素的想法是用递归的方式一层层修改（类似于线段树的建立），但这样的时间复杂度比较高。使用懒标记后，对于那些正好是线段树节点的区间，我们不继续递归下去，而是打上一个标记，将来要用到它的子区间的时候，再向下传递。

void update(ll l, ll r, ll d, ll p = 1, ll cl = 1, ll cr = n)
{    //l表示目标区间下限，r表示目标区间上限，d表示增加的数，p表示遍历节点的动态下标
     //cl和cr分别表示当前节点的区间上下限
    if (cl > r || cr < l) // 区间无交集
        return; // 剪枝
    else if (cl >= l && cr <= r) // 当前节点对应的区间包含在目标区间中
    {
        tree[p] += (cr - cl + 1) * d; // 更新当前区间的值
        if (cr > cl) // 如果不是叶子节点
            mark[p] += d; // 给当前区间打上标记
    }
    else // 与目标区间有交集，但不包含于其中
    {
        ll mid = (cl + cr) / 2;    //对节点包含的区间进行二分
        mark[p * 2] += mark[p]; // 标记向下传递
        mark[p * 2 + 1] += mark[p];
        tree[p * 2] += mark[p] * (mid - cl + 1); // 往下更新一层
        tree[p * 2 + 1] += mark[p] * (cr - mid);
        mark[p] = 0; // 清除标记
        update(l, r, d, p * 2, cl, mid); // 递归地往下寻找
        update(l, r, d, p * 2 + 1, mid + 1, cr);
        tree[p] = tree[p * 2] + tree[p * 2 + 1]; // 根据子节点更新当前节点的值
    }
}

更新时，我们是从最大的区间开始，递归向下处理。注意到，任何区间都是线段树上某些节点的并集。于是我们记目标区间为[l,r]，当前区间为[cl,cr]，当前节点为p，我们会遇到三种情况：

1. 当前区间与目标区间没有交集：

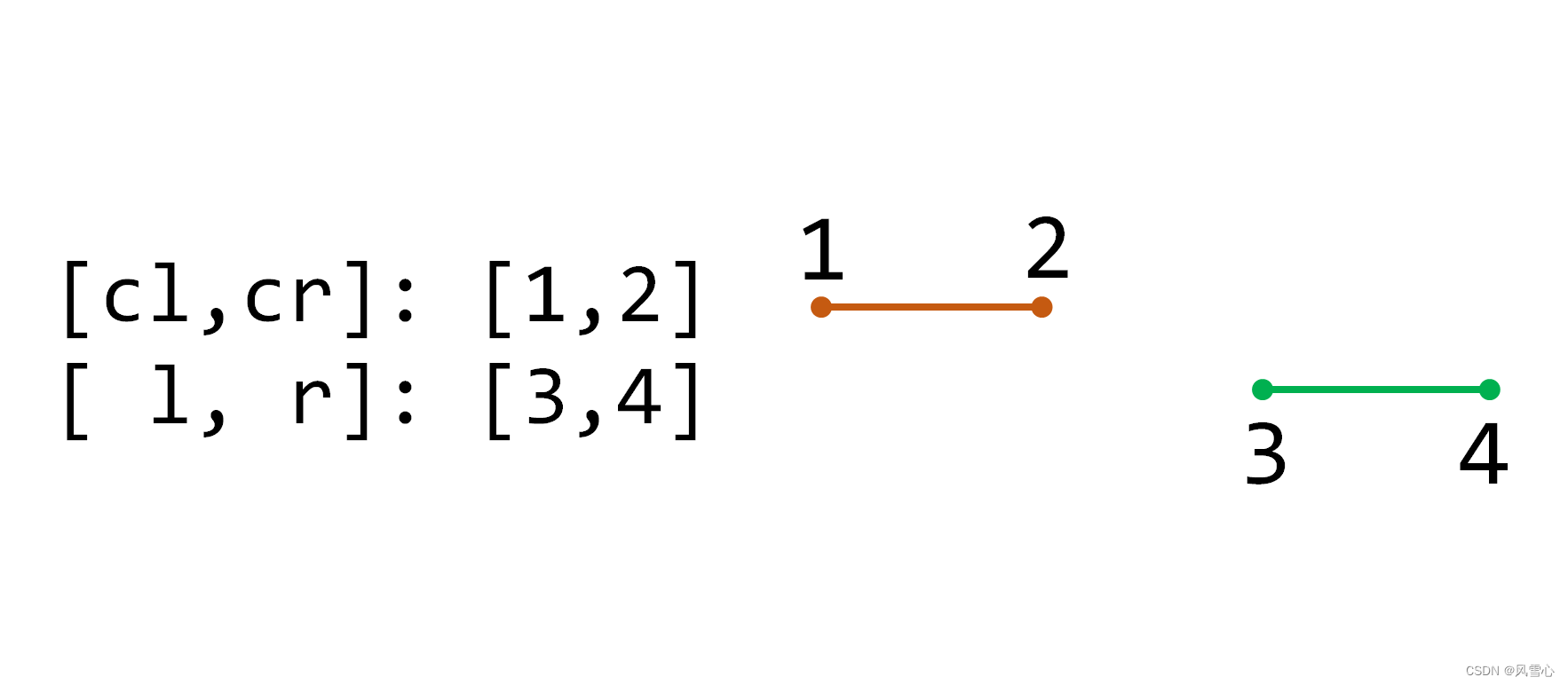
这时直接结束递归。

2.当前区间被包括在目标区间里：

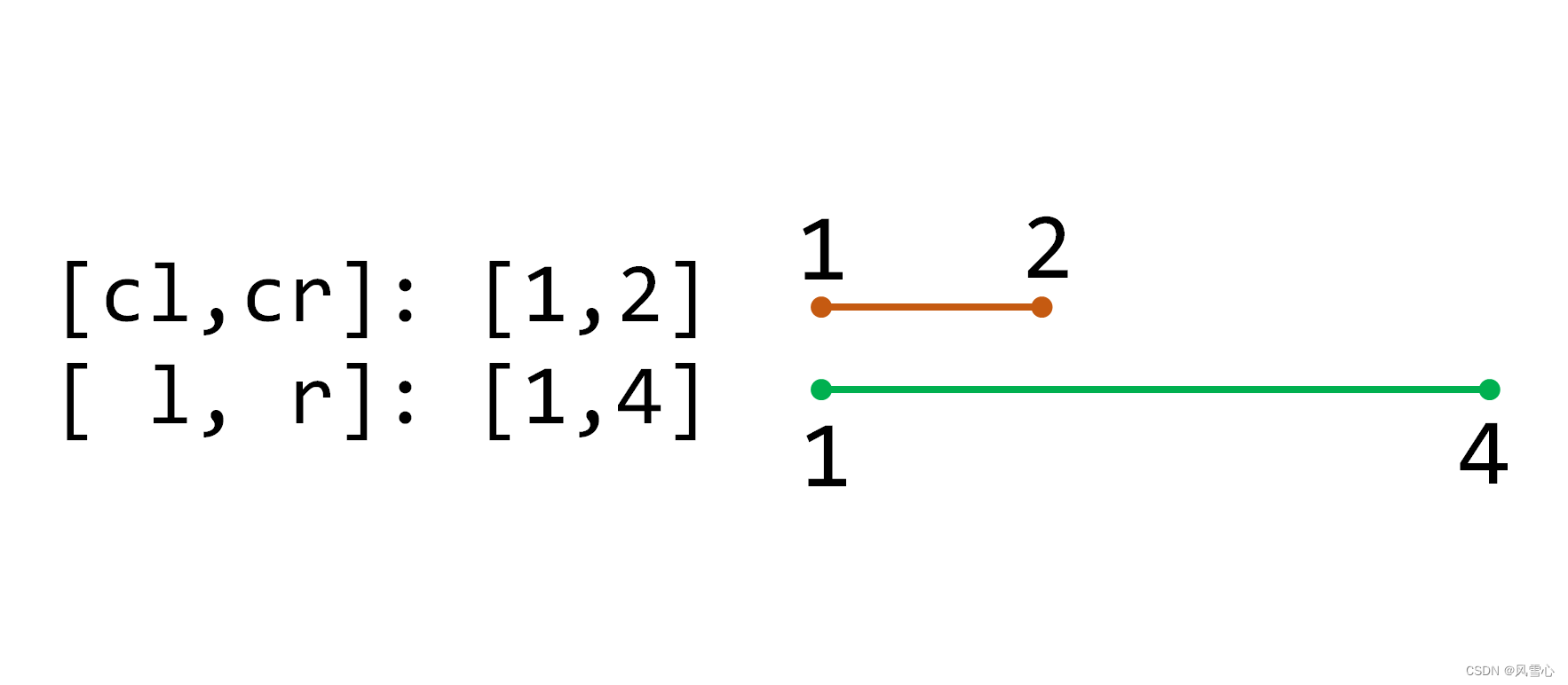
这时可以更新当前区间，别忘了乘上区间长度：

tree[p] += (cr - cl + 1) * d;

然后打上懒标记（叶子节点可以不打标记，因为不会再向下传递了）：

mark[p] += d;

这个标记表示“该区间上每一个点都要加上d”。因为原来可能存在标记，所以是+=而不是=。

3.当前区间与目标区间相交，但不包含于其中：

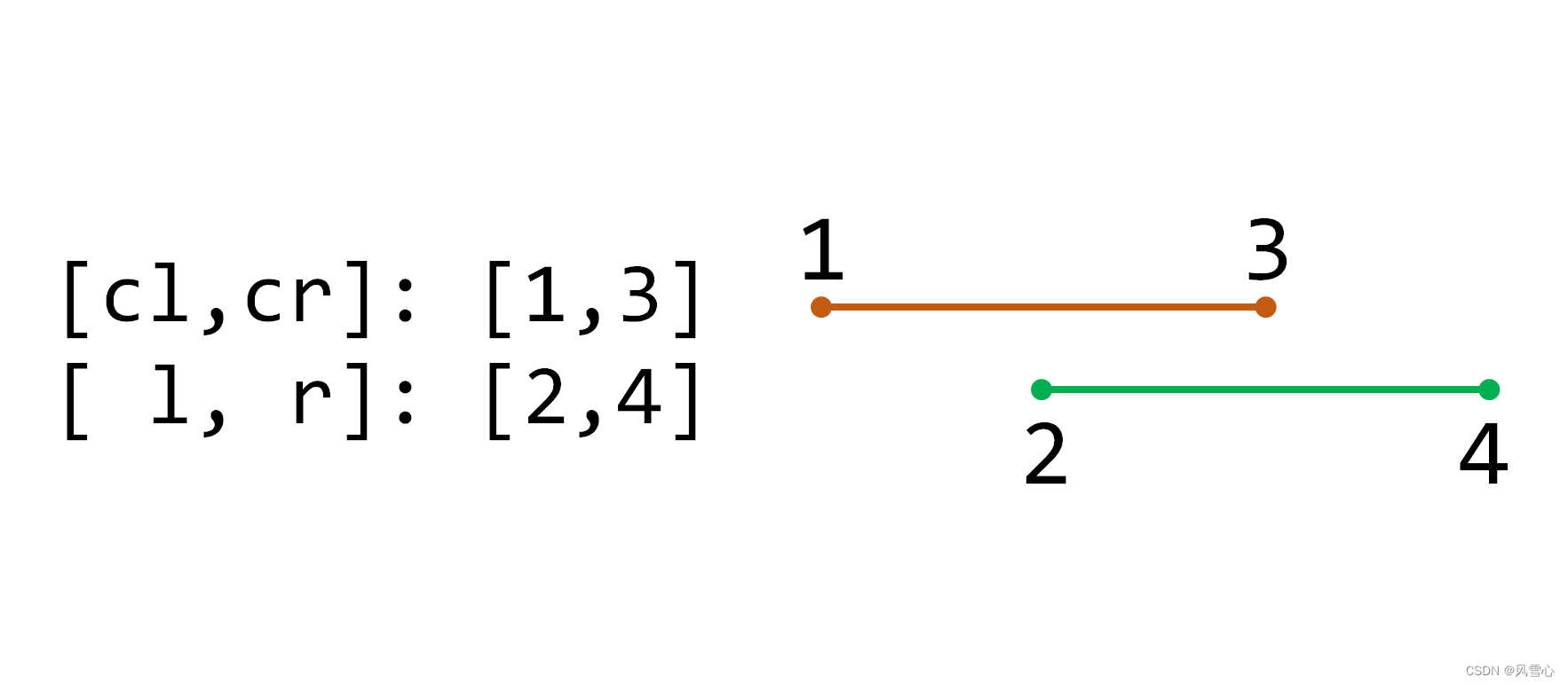
这时把当前区间一分为二，分别进行处理。如果存在懒标记，要先把懒标记传递给子节点（注意也是+=，因为原来可能存在懒标记）：

ll mid = (cl + cr) / 2;
mark[p * 2] += mark[p];
mark[p * 2 + 1] += mark[p];

两个子节点的值也就需要相应的更新（后面乘的是区间长度）：

tree[p * 2] += mark[p] * (mid - cl + 1);
tree[p * 2 + 1] += mark[p] * (cr - mid);

不要忘记清除该节点的懒标记：

mark[p] = 0;

这个过程并不是递归的，我们只往下传递一层（所以叫“懒”标记啊！），以后要用再才继续传递。其实我们常常把这个传递过程封装成一个函数：

inline void push_down(ll p, ll len)
{
    mark[p * 2] += mark[p];
    mark[p * 2 + 1] += mark[p];
    tree[p * 2] += mark[p] * (len - len / 2);
    tree[p * 2 + 1] += mark[p] * (len / 2); // 右边的区间可能要短一点
    mark[p] = 0;
}

然后在update函数中这样调用：

push_down(p, cr - cl + 1);

传递完标记后，再递归地去处理左右两个子节点。

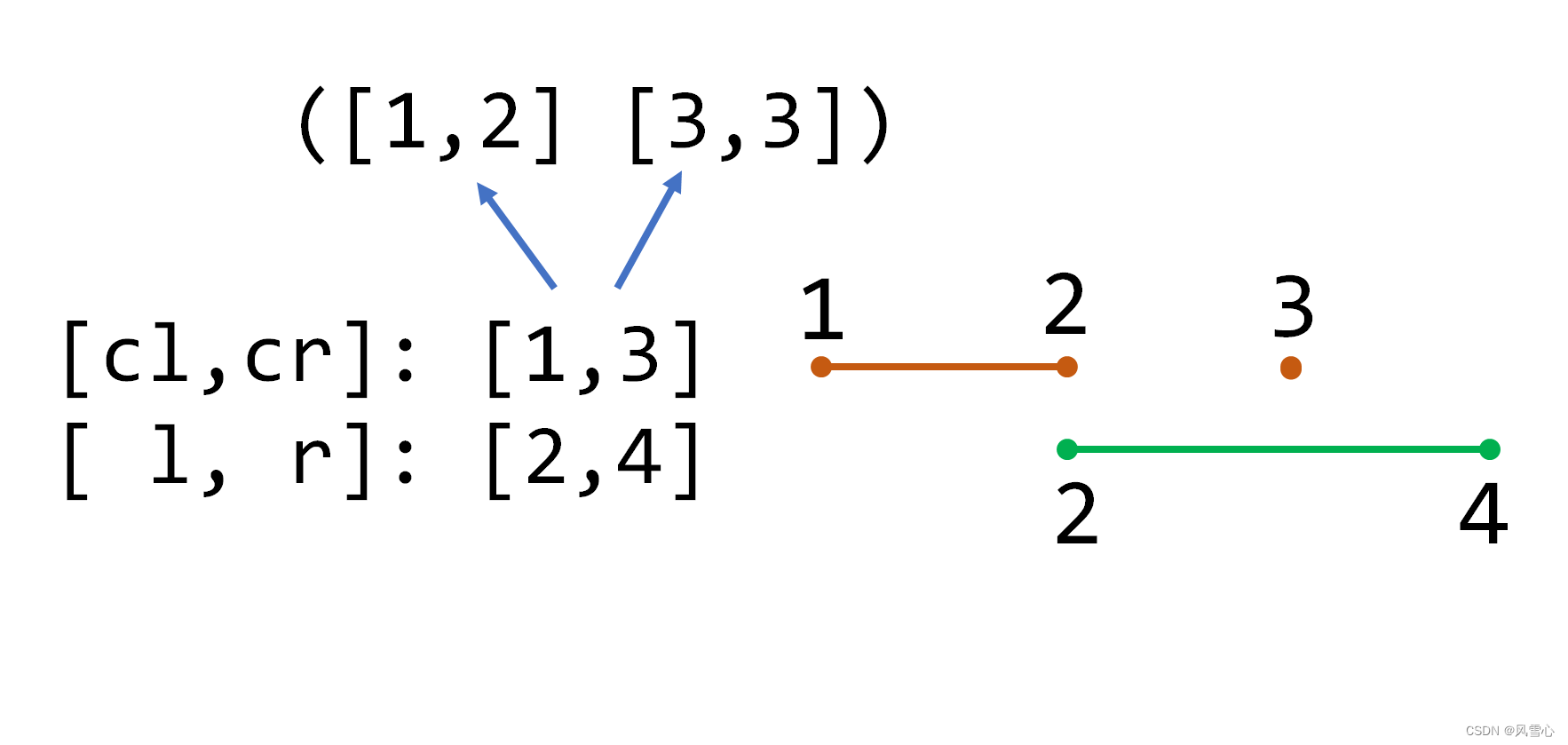
至于单点修改，只需要令左右端点相等即可。

五、线段树的区间查询

有了区间修改的经验，区间查询的方法完全类似，直接上代码了：

ll query(ll l, ll r, ll p = 1, ll cl = 1, ll cr = n)
{
    if (cl > r || cr < l)
        return 0;
    else if (cl >= l && cr <= r)
        return tree[p];
    else
    {
        ll mid = (cl + cr) / 2;
        push_down(p, cr - cl + 1);
        return query(l, r, p * 2, cl, mid) + query(l, r, p * 2 + 1, mid + 1, cr); 
        // 上一行拆成三行写就和区间修改格式一致了
    }
}

一样地递归，一样自顶至底地寻找，一样地合并信息。

六、模板题代码实现

#include <bits/stdc++.h>
#define MAXN 100005
using namespace std;
typedef long long ll;
inline ll read()    //快读快输
{
    ll ans = 0;
    char c = getchar();
    while (!isdigit(c))
        c = getchar();
    while (isdigit(c))
    {
        ans = ans * 10 + c - '0';
        c = getchar();
    }
    return ans;
}
ll n, m, A[MAXN], tree[MAXN * 4], mark[MAXN * 4]; // 经验表明开四倍空间不会越界
inline void push_down(ll p, ll len)
{
    mark[p * 2] += mark[p];
    mark[p * 2 + 1] += mark[p];
    tree[p * 2] += mark[p] * (len - len / 2);
    tree[p * 2 + 1] += mark[p] * (len / 2);
    mark[p] = 0;
}
void build(ll l = 1, ll r = n, ll p = 1)
{
    if (l == r)
        tree[p] = A[l];
    else
    {
        ll mid = (l + r) / 2;
        build(l, mid, p * 2);
        build(mid + 1, r, p * 2 + 1);
        tree[p] = tree[p * 2] + tree[p * 2 + 1];
    }
}
void update(ll l, ll r, ll d, ll p = 1, ll cl = 1, ll cr = n)
{
    if (cl > r || cr < l)
        return;
    else if (cl >= l && cr <= r)
    {
        tree[p] += (cr - cl + 1) * d;
        if (cr > cl)
            mark[p] += d;
    }
    else
    {
        ll mid = (cl + cr) / 2;
        push_down(p, cr - cl + 1);
        update(l, r, d, p * 2, cl, mid);
        update(l, r, d, p * 2 + 1, mid + 1, cr);
        tree[p] = tree[p * 2] + tree[p * 2 + 1];
    }
}
ll query(ll l, ll r, ll p = 1, ll cl = 1, ll cr = n)
{
    if (cl > r || cr < l)
        return 0;
    else if (cl >= l && cr <= r)
        return tree[p];
    else
    {
        ll mid = (cl + cr) / 2;
        push_down(p, cr - cl + 1);
        return query(l, r, p * 2, cl, mid) + query(l, r, p * 2 + 1, mid + 1, cr);
    }
}
int main()
{
    n = read();
    m = read();
    for (int i = 1; i <= n; ++i)
        A[i] = read();
    build();
    for (int i = 0; i < m; ++i)
    {
        ll opr = read(), l = read(), r = read();
        if (opr == 1)
        {
            ll d = read();
            update(l, r, d);
        }
        else
            printf("%lld\n", query(l, r));
    }
    return 0;
}

更加紧凑的版本：

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int MAXN = 1e5 + 5;
ll tree[MAXN << 2], mark[MAXN << 2], n, m, A[MAXN];
void push_down(int p, int len)
{
    if (len <= 1) return;
    tree[p << 1] += mark[p] * (len - len / 2);
    mark[p << 1] += mark[p];
    tree[p << 1 | 1] += mark[p] * (len / 2);
    mark[p << 1 | 1] += mark[p];
    mark[p] = 0;
}
void build(int p = 1, int cl = 1, int cr = n)
{
    if (cl == cr) return void(tree[p] = A[cl]);
    int mid = (cl + cr) >> 1;
    build(p << 1, cl, mid);
    build(p << 1 | 1, mid + 1, cr);
    tree[p] = tree[p << 1] + tree[p << 1 | 1];
}
ll query(int l, int r, int p = 1, int cl = 1, int cr = n)
{
    if (cl >= l && cr <= r) return tree[p];
    push_down(p, cr - cl + 1);
    ll mid = (cl + cr) >> 1, ans = 0;
    if (mid >= l) ans += query(l, r, p << 1, cl, mid);
    if (mid < r) ans += query(l, r, p << 1 | 1, mid + 1, cr);
    return ans;
}
void update(int l, int r, int d, int p = 1, int cl = 1, int cr = n)
{
    if (cl >= l && cr <= r) return void(tree[p] += d * (cr - cl + 1), mark[p] += d);
    push_down(p, cr - cl + 1);
    int mid = (cl + cr) >> 1;
    if (mid >= l) update(l, r, d, p << 1, cl, mid);
    if (mid < r) update(l, r, d, p << 1 | 1, mid + 1, cr);
    tree[p] = tree[p << 1] + tree[p << 1 | 1];
}
int main()
{
    ios::sync_with_stdio(false);
    cin >> n >> m;
    for (int i = 1; i <= n; ++i)
        cin >> A[i];
    build();
    while (m--)
    {
        int o, l, r, d;
        cin >> o >> l >> r;
        if (o == 1)
            cin >> d, update(l, r, d);
        else
            cout << query(l, r) << '\n';
    }
    return 0;
}

风雪心

关注

23
点赞
踩
30

收藏

觉得还不错? 一键收藏
打赏
1
评论
【算法】线段树

几乎是算法竞赛最常用的数据结构了，它主要用于（要求满足结合律）。与树状数组相比，它可以实现的，还可以同时（加、乘），更具通用性。如题，已知一个数列，你需要进行下面两种操作：1.将某区间每一个数加上x2.求出某区间每一个数的和第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。
复制链接

扫一扫