二维线性 DP-例题分析笔记(含 24年蓝桥真题)

例1：数字金字塔

题目描述：

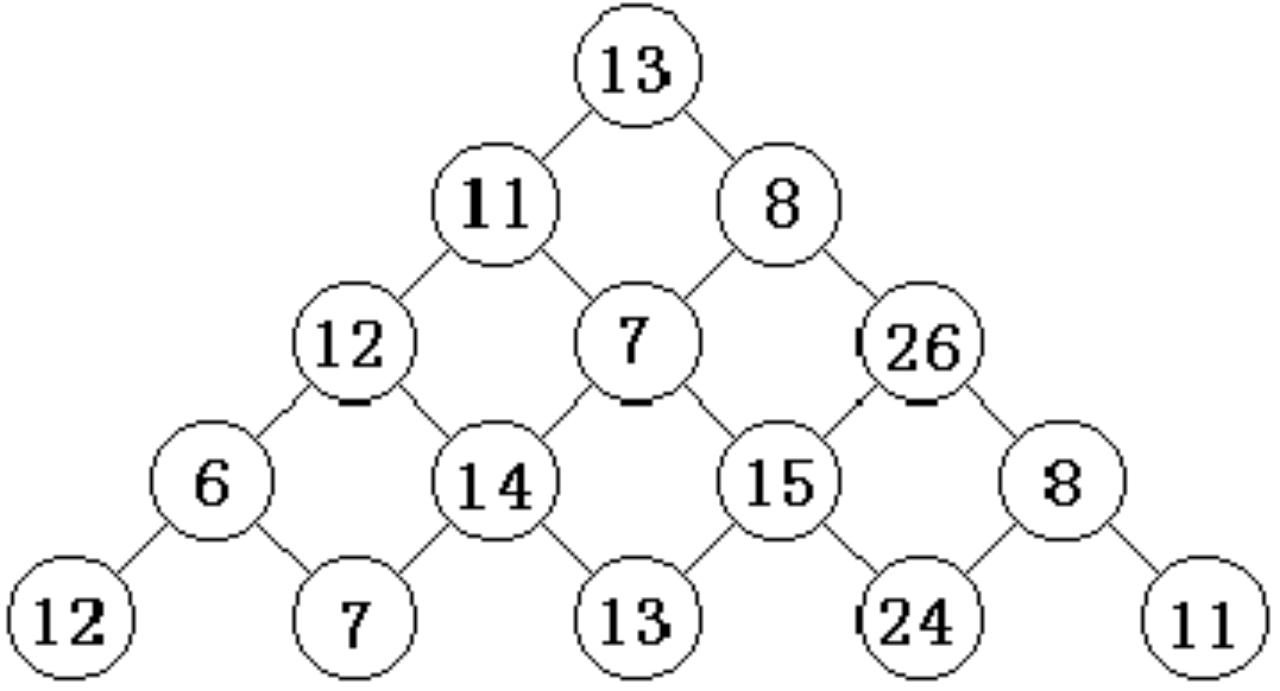
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。

输入：

       第一个行包含R(1<= R<=1000)，表示行的数目。

       后面每行为这个数字金字塔特定行包含的整数。

       所有的被供应的整数是非负的且不大于100。

输出：

      单独的一行，包含那个可能得到的最大的和。

样例输入：

5

13

11   8

12  7   26

6  14   15   8

12  7   13  24   11

样例输出：

86

---

普通搜索解法：

题目分析：题目要求从按照规则从最高点走到最低点的最大权值和，路径的起点和终点是固定的，那么我们就可以用搜索来解决，搜索每一条路径的权值和，然后去最大值。

1.直接定义一个递归函数：dfs(int x, int y, int currWeight) ，其中 x ，y 表示从（1, 1）走到（x， y）这条路径上的权值和是 currWeight。

2.当x 等于 N 时，即已经走到了第 N 行，也即递归函数的结束处，此时我们只需要判断，currWeight 是否大于 ans （这个变量是用来记录最终输出的答案的，即最大权值和，因为求最大值，一般赋值为负数，这里将其赋值为 ans = INT_MIN，即int 类型的最小值），如果 currWeight 大于 ans 则更新 ans 的值为 currWeight； 否则按下面两个方向走，即执行递归函数dfs(x+1, y, nums[x+1][y] + currWeight) 和 dfs(x+1, y+1, currWeight + nums[x+1][y+1])。nums数组存储的是该金字塔的每个数。

完整代码如下：

#include<bits/stdc++.h>
using namespace std;

const int maxn = 1e5+10;
int ans = INT_MIN;
int n;
int nums[maxn][maxn];
void dfs(int x, int y, int currWeight){
    if(x == n){ // 结束条件
        if(currWeight > ans){
            ans = currWeight; // 更新答案
        }
        return;
    }
    dfs(x+1, y, currWeight + nums[x+1][y]);
    dfs(x+1, y+1, currWeight + nums[x+1][y+1]);
}

int main(){
    cin >> n;
    for(int i=1; i<=n; i++){
        for(int j=1;j<=i; j++)
            cin >> nums[i][j];
    }
    //  搜索
    dfs(1, 1, nums[1][1]);
    cout << ans << endl;
    
    return 0;
}

综上，可知其时间复杂度为 O(2^n)，如果数据规模过大，则不推荐这种写法）会超时！

---

记忆搜索解法：

首先我们先普通分析一下上述普通搜索的超时原因之：

上述搜索之所以会超时，是因为进行了重复搜索，如样例中从(1,1)到(3,2)有“左右”和“右左”两种不同的路径，即搜索过程中两次到达(3,2)这个位置，那么从(3,2)走到终点的每一条路径就被搜索了两次，我们完全可以在第一次搜索(3,2)到终点的路径时就记录下(3,2)到终点的最大权值和，下次再次来到(3,2)时就可以直接调用这个权值避免重复搜索。我们把这种方法称为记忆化搜索，这也是记忆搜索的精髓所在。

​​​​​​​定义 dfs(int x, int y): 

表示从(x, y) 出发到达终点的最大权值和，则答案就是 dfs(1, 1)。在计算 dsf(x, y)时我们考虑从向左和向右两个方向。（请牢记这个定义，看不懂代码请反复理解一下这个定义）​​​​​​​

1.第一步向左：那么根据题意和分析可以得出，从 (x, y) 到终点的这条路径就被分成了两部分，即先从(x, y) 到(x+1, y) 接着由 (x+1, y) 到终点。那么第一部分就是固定的权值，即 nums[x][y]，第二部分的就是剩下路径的最大权值和，即 dfs(x+1, y)。

综上，第一步向左的的路径最大权值和就是 : dfs(x+1, y) + nums[x][y]

2.第二步向右：同理，向右也可以分为两部分，即先从 (x, y) 到 (x+1, y+1)，再从 (x+1, y+1) 到终点。

综上，第二步向右的路径最大权值和就是：nums[x][y] + dfs(x+1, y+1)

为了避免重复计算，我们用一个全局数组 flag[x][y]，记录从 (x, y) 出发到达终点的最大权值和，一开始随便赋值一个负数就可了，这里我们统一赋值为 -1，在计算 dfs(x, y) 时，我们首先查询 flag[x][y]，如果其值不等于-1，则说明 dfs(x, y) 已经被计算过了， 直接返回 flag[x][y]即可，否则计算 dfs(x, y)的值并存储在 flag[x][y]中。

完整代码如下：

#include<bits/stdc++.h>
using namespace std;

const int Maxn = 505;
int flag[Maxn][Maxn];
int nums[Maxn][Maxn];
int n;
int dfs(int x, int y);

int main(){
    // 数据输入以及预处理将 flag 数组赋值为 -1
    cin >> n;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=i; j++){
            cin >> nums[i][j];
        }
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=i; j++){
            flag[i][j] = -1;
        }
    }
    dfs(1, 1);
    cout << flag[1][1] << endl;
    // 也可以像下面这样直接打印结果,结果，由 dfs（x，y）的定义得
//    cout << dfs(1, 1) << endl;
    return 0;
}
int dfs(int x, int y){
    if(flag[x][y] == -1){
        if(x == n)
            // 如果是后一行元素，则 flag[x][y] = nums[x][y],
            // 因为这就好比从从 点 （x, y) 的上一个点到 （x， y)这个点的权值为多少，不就是点（x，y）对应的值嘛
            flag[x][y] = nums[x][y];
        else
            // 如果不是到最后一行，那么则有左右条路可以走，选其权值和的最大值，再加上该点对应的权值
            flag[x][y] = nums[x][y] + max(dfs(x+1, y), dfs(x+1, y+1));
    }
//    如果 flag[x][y]不等于 -1 说明之前已经计算出了从该点到终点的最大权值之和，则直接返回即可
    return flag[x][y];
}

综上，可知这段代码主要是通过深度优先搜索（DFS）来计算从顶点到最后一行的最大权值和。对于每个位置 (x, y) ，最多会被计算两次（一次从左边递归过来，一次从右边递归过来）。所以时间复杂度为 O(n^2) 。

---

重头戏来喽！～动态规划解法:

经过上面两种方法的理解和学习，我相信到这，再来学习进阶的动态规划解法是完全 so easy！

下面按动态规划迭代实现法进行讲解：

1.状态确定：题目要求从（1,1）出发到达最后一行的某个位置这个路径的最大权值和，即起点是确定的，而终点和路径中经过的点是不确定的。

因此我们定义 dp[x][y] 表示从（1,1）出发到达点 （x，y）的最大路径权值和，

则最终答案为： ans=max（dp[n][1],dp[n][2]...dp[n][n])

2.确定状态转移方程和边界条件：

思考时：我们不用去考虑(1,1)到(x,y)的每一步是如何走的，只需要考虑最后一步是如何走的，根据最后一步是向左还是向右分成以下两种情况：

向左：最后一步是从（x-1，y）走到（x，y），则此路径被分为两部分，第一部分是从 （1,1）走到（x-1，y），第二部分是从（x-1，y）走到（x，y）。该路径的最大权值和可以表示为，第一部分的最大权值和，加上第二部分的权值即加上 nums[x][y]，而第一部分的最大权值和就是从（1,1）到（x-1，y）的路径最大权值和，就是 dp 数组的定义，所以第一部分的路径最大权值和就是 dp[x-1][y]

综上，该路径最大权值和为：dp[x-1][y]+nums[x][y]

向右：与向左类似，即最后一步是从（x-1，y-1）走到（x，y），则此路径被分为两部分，第一部分是从 （1,1）走到（x-1，y-1），第二部分是从（x-1，y-1）走到（x，y）。

综上，同理的该路径最大权值和为：dp[x-1][y-1]+nums[x][y]

综上得状态转移方程为：

dp[x][y] = max( dp[x-1][y], dp[x-1][y-1] ) + nums[x][y]

根据 dp 数组的定义，其边界条件就是：dp[1][1] = nums[1][1]

这里正式介绍一种迭代法。与分析边界条件方法相似，计算dp[x][y]用到状态dp[x-1][y-1]与dp[x-1][y]，这些元素在dp[x][y]的上一行，也就是说要计算第x行的状态的值，必须要先把第x-1行元素的值计算出来，因此我们可以先把第一行元素 dp[1][1] 赋为 nums[1][1]，再从第二行开始按照行递增的顺序计算出每一行的有效状态即可。时间复杂度为O(n^2)。

注意：

根据 dp 数组的定义即：dp[x][y]表示从（1,1）到 （x，y）的路径最大权值和，由此可知我们是无法直接求得其最终结果路径最大权值和的，所以我们需要如下操作：

即定义一个变量存储最终答案，并遍历最后一行的元素求其 dp[n][i]，其每个值都是到终点的一个路径权值和，而我们只需取他们这些答案中最大的一个就是我们需要的最终答案了。

int ans = 0;
    for(int i=1; i<=n; i++){
        int tmp = dfs(n ,i);
        if(tmp > ans)
            ans = tmp;
    }

完整代码如下：

#include<bits/stdc++.h>
using namespace std;

const int maxn = 505;
//  dp[x][y] 表示从（1,1）出发到达点 （x，y）的最大路径权值和
int nums[maxn][maxn],dp[maxn][maxn];
int n;
int dfs(int x, int y){
    if(dp[x][y] == -1){
         dp[x][y] = nums[x][y] + max(dfs(x-1, y), dfs(x-1, y-1));
    }
    return dp[x][y];
}
int main(){
    cin >> n;
    for(int i=1; i<=n; i++){
        for(int j=1; j<=i; j++){
            cin >> nums[i][j];
        }
    }
    for(int i=1; i<=n; i++){
        for(int j=1; j<=i; j++){
            dp[i][j] = -1;
        }
    }
//    dp[1][1] = nums[1][1];
    int ans = 0;
    for(int i=1; i<=n; i++){
        int tmp = dfs(n ,i);
        if(tmp > ans)
            ans = tmp;
    }
    cout << ans << endl;

    return 0;
}

---

例2：数字串个数（2024 年蓝桥杯省赛Python B 组填空题）

题目描述：

小蓝想要构造出一个长度为 10000 的数字字符串，有以下要求：

1) 小蓝不喜欢数字 0 ，所以数字字符串中不可以出现 0 ；

2) 小蓝喜欢数字 3 和 7 ，所以数字字符串中必须要有 3 和 7 这两个数字。

请问满足题意的数字字符串有多少个？这个数字会很大，你只需要输出其

对 109 + 7 取余后的结果。​​​​​​​

---

题目分析：

该题规模如果直接暴力搜索时间复杂度明显超时了，可能从比赛开始跑，知道比赛结束都还跑不完，说明这不是他想考我们的点，换一个思维，该题明显也不是贪心...

大 哥，我确实看不出怎么做了，考啥都不知道嘛！咋办呢？一般到这，就是不知到考啥，且常规的搜索、贪心等算法都用不了，那么就基本是dp了，可以往动态规划这方面思考！

上正题咯：

首先我们先定义一个数组：long long ans[10001][4],

数组定义：

• 第一个维度表示字符串的长度（从 1 到 10000）。
• 第二个维度的 4 个元素分别代表：
  • ans[i][0]：到长度为 i 时含 3 的情况数。
  • ans[i][1]：到长度为 i 时含 7 的情况数。
  • ans[i][2]：到长度为 i 时既不含 3 也不含 7 的情况数。
  • ans[i][3]：到长度为 i 时同时含 3 和 7 的情况数。

数组初始化：long long ans[10001][4] = { {0,0,0,0}, {1, 1, 7, 0} }

原因如下：

        长度为 i 为 0 时，自然其第二维度的每个值都没有意义即任意赋值对其结果都不会有影响这里统一将其全赋值为 0。

• ans[10001][4] 中的 4 个元素分别代表不同的状态。
• ans[1][0] = 1 表示数字串长度为 1 时，只含 3 没有 7 的情况有一种（即只有 3 本身）。
• ans[1][1] = 1 表示数字串长度为 1 时，只含 7 没有 3 的情况有一种（即只有 7 本身）。
• ans[1][2] = 7 表示数字串长度为 1 时，既不含 3 也不含 7 的情况有 7 种（因为除了 3 和 7 还有 1、2、4、5、6、8、9 这 7 个数字可选）。
• ans[1][3] = 0 表示数字串长度为 1 时，同时含 3 和 7 的情况还没有。

接下来我们来看其递推公式：

1.只含 3 没有 7 的情况：

ans[i][0] = ans[i-1][2] + ans[i-1][0]*7 + ans[i-1][1];

我们来分析一下各项的含义：

• ans[i-1][2]：表示前一个长度时既不含 3 也不含 7 的情况数。当在此基础上添加一个数字时，有可能添加 3 从而变成当前长度下含 3 的情况。
• ans[i-1][0]*7：表示前一个长度时已经含 3 的情况，由于还可以添加 7 种其他非 0、3、7 的数字，所以有这么多种扩展方式。
• ans[i-1][1]：表示前一个长度时含 7 的情况，同样可以添加其他数字来扩展。

2.只含 7 没有 3 的情况：

ans[i][1] = ans[i-1][0] + ans[i-1][1]*7 + ans[i-1][2];

我们来分析一下各项的含义：

• ans[i-1][0]：前一个长度下含 3 的情况，在此基础上添加数字 7 就变成当前长度下含 7 的新情况。
• ans[i-1][1]*7：前一个长度下已经含 7 的情况，还可以再添加 7 种非 0、3、7 的数字来扩展出更多含 7 的情况。
• ans[i-1][2]：前一个长度下既不含 3 也不含 7 的情况，在此基础上添加数字 7 就得到当前长度下新的含 7 的情况。

3.既不含 3 也不含 7：

ans[i][2] = ans[i-1][2]*7;

分析如下​​​​​​​:

        ans[i-1][2]*7：表示前一个长度为时既不含 3 也不含 7 的情况，在此基础上还想让其下一个长度的数字串同时不含 3 和 7 就只有 7 种情况了，添加 1,3,4,5,6,8,9这 7 位数字中的任意一个。

4.既包含 3 也包含 7：

ans[i][3] = ans[i-1][0] + ans[i-1][1] + ans[i-1][3]*9; 

我们来分析一下各项的含义：

• ans[i-1][0]：表示前一个长度时含 3 的情况，在此基础上再添加一个合适的数字（不能是 0）就可能得到同时含 3 和 7 的新情况。
• ans[i-1][1]：表示前一个长度时含 7 的情况，同理也是可以发展为同时含 3 和 7 的情况。
• ans[i-1][3]*9：之前已经是同时含 3 和 7 的情况，还可以再添加 9 个非 0 的数字（因为题目要求数字串中不能出现 0）来进一步扩展这种情况，即 9 种情况。

完整代码如下：

#include<bits/stdc++.h>
using namespace std;

long long ans[10001][4]={{0,0,0,0},{1,1,7,0}};
const int MOD=1000000007;

int main(){
    int i;
    for(i=2; i<=10000; i++){

// 每个递推公式都用 MOD 求余数，避免在递推过程中就结果溢出，导致最终结果受出错
        ans[i][0] = (ans[i-1][2] + ans[i-1][0] * 7 + ans[i-1][1]) % MOD;
        ans[i][1] =(ans[i-1][0] + ans[i-1][1] * 7 + ans[i-1][2]) % MOD;
        ans[i][2] = (ans[i-1][2] * 7) % MOD;
        ans[i][3] = (ans[i-1][0] + ans[i-1][1] + ans[i-1][3] * 9) % MOD;
    }
// 注意：应该输出 i-1 而不是 i，因为循环结束时 i 已经超出范围
    cout << (ans[i-1][0] + ans[i-1][1] + ans[i-1][3]) % MOD << endl;
    return 0;
}