2022第十三届蓝桥杯省赛C++A组：最长不下降子序列（二维动态规划解法）

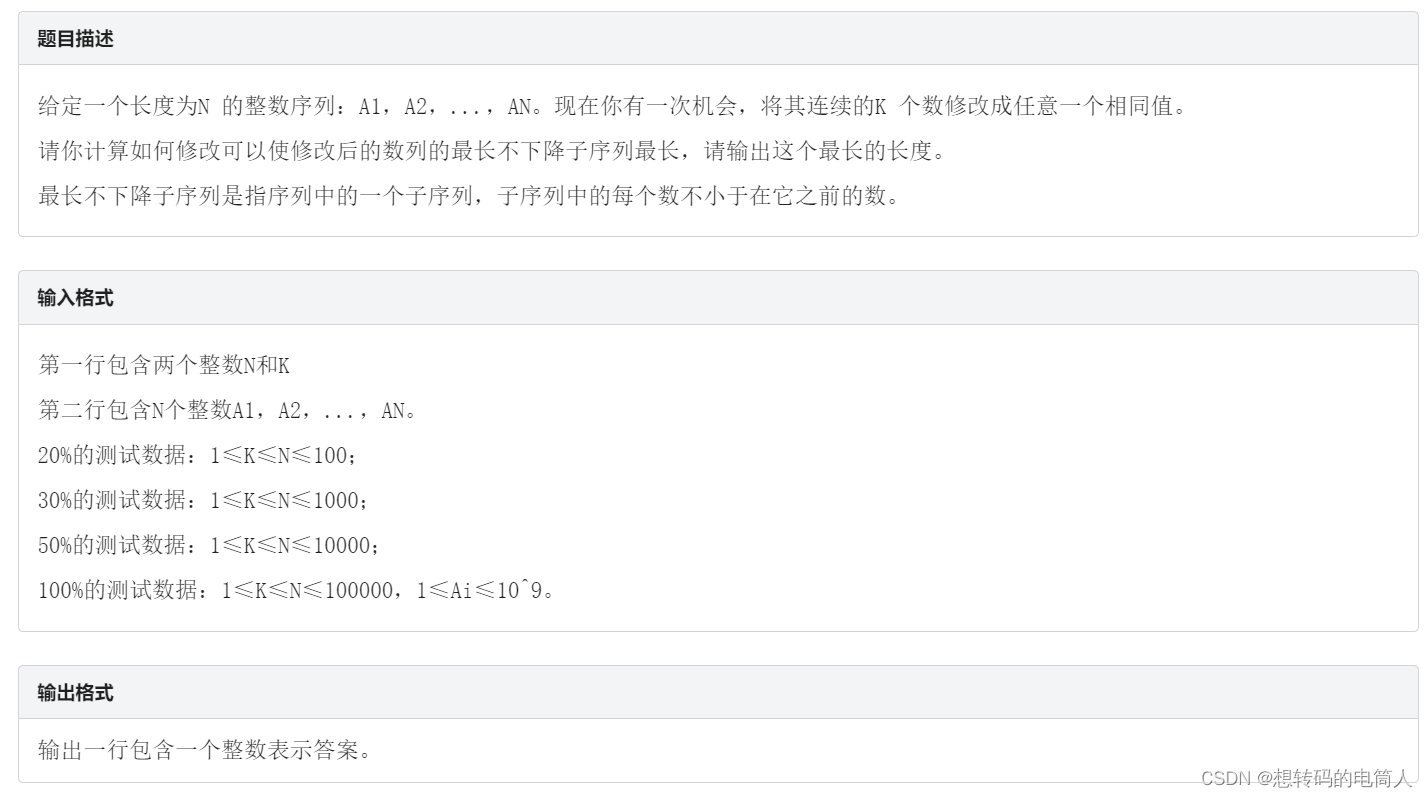
题目描述

笔者认为该题目有些问题，序列应该是可以不连续的，不过这个题目是按连续子序列来的，那就按要求做了

解题思路

对于该题考虑二维动态规划，dp[i]用来表示以nums[i]为结尾的序列，其最长不下降的序列长度，dp[i][0]代表没有修改过的序列，dp[i][1]代表已修改过的序列，初始状态dp[0][0]=dp[0][1]=1

用一个序列进行举例 5 6 26 23 22 21 27 10 k=3该序列最长不下降子序列长度为7

对该数组用两次循环进行遍历

对于nums[i]<=nums[j]，动态转移方程为

dp[j][0] = max(dp[i][0] + 1, dp[j][0])，未修改的最长子序列长度+1
dp[j][1] = max(dp[i][1] + 1, dp[j][1])，已修改的最长子序列长度+1

即在原本dp[i]的最长子序列上加1，本例中5,6,26即为以26结尾的最长子序列，dp[2][0]=dp[2][1]=3

对于nums[j]>nums[i]，需要执行三步，

第一步，dp[j][1] = max(dp[i][0] + 1, dp[j][1]);即未修改的状态->已修改的状态，例如5 6 26 23 直接修改为5 6 26 26，故以nums[3]=23结尾的已修改的最长子序列长度为4

第二步，k=3，从nums[3]开始的3个数均可改为nums[2]=26，故dp[i + t][1] = max(dp[i][0] + t, dp[i + t][1])，其中1<=t<=k，即以23,22,21结尾的最长子序列均可在前面基础上+1，即改成5 6 24 24 24 24，此时最长子序列长度为6

第三步，从21改为26继续往后遍历，后面27比26大，故以27结尾的子序列长度再+1，为7，往后碰到10，比26小，终止遍历

最终dp[i][1]中含有最佳状态，在本例中最佳状态以27结尾即dp[6][1]=7

#include<bits/stdc++.h>
using namespace std;
int N, k;
vector<int> nums;
int main() {
	cin >> N >> k;
	vector<int> t(2, 1);
	vector<vector<int>> dp(N, t);
	while (N--) {
		int temp;
		cin >> temp;
		nums.push_back(temp);
	}
	for (int i = 0; i < nums.size(); i++) {
		int j = i + 1;
		for (int j = i + 1; j < nums.size(); j++) {
			if (nums[i] <= nums[j])
			{
				dp[j][0] = max(dp[i][0] + 1, dp[j][0]);
				dp[j][1] = max(dp[i][1] + 1, dp[j][1]);
			}
			else {
				dp[j][1] = max(dp[i][0] + 1, dp[j][1]);
				for (int t = 1; t <= k && i + t < nums.size(); t++) {
					dp[i + t][1] = max(dp[i][0] + t, dp[i + t][1]);
				}
				for (int t = i + k + 1; t < nums.size(); t++) {
					if (nums[i] <= nums[t])
						dp[t][1] = max(dp[i][0] + t - i, dp[t][1]);
					else break;
				}
				break;
			}
		}
		/*cout << i << endl;
		for (auto d : dp) {
			for (auto p : d) {
				cout << p << " ";
			}
			cout << endl;
		}*/
	}
	int m = 0;
	for (int i = 0; i < nums.size(); i++)
		m = max(m, dp[i][1]);
	cout << m;
	return 0;
}