重新开始学stm32 控制算法 —— PID算法

上山的路

已于 2023-09-18 21:42:28 修改

阅读量5.5k

点赞数 13

文章标签：服务器 linux 运维

于 2023-08-30 22:32:20 首次发布

本文链接：https://blog.csdn.net/weixin_73719155/article/details/132589802

版权

今天我们来学习新的内容 —— PID算法。想必大家都听说过 PID 算法的鼎鼎大名了，今天我们就从增量式 PID 和位置式 PID 这两种来认识这个非常实用且通用的控制算法。

简介

首先，我们还是先来简单了解一下什么是 PID 。

PID即：Proportional（比例）、Integral（积分）、Differential（微分）的缩写。PID 的使用场景非常广泛，凡是需要将某个物理量保持稳定的场景，PID 都可以大显神通。像它的名字一样，它的组成部分有三个部分：比例部分、积分部分、微分部分。

1.比例（P）部分

成比例地反映控制系统的偏差信号 e(t)，偏差一旦产生，控制器立即产生控制作用，以减小偏差。当仅有比例控制时系统输出存在稳态误差。P 参数越大比例作用越强，动态响应越快，消除误差的能力越强。但实际系统是有惯性的，控制输出变化后，实际 u(t) 值变化还需等待一段时间才会缓慢变化。所以，由于实际系统是有惯性的，比例作用不宜太强，比例作用太强会引起系统振荡不稳定。P 参数的大小应在以上定量计算的基础上根据系统响应情况，现场调试决定，通常将P参数由大向小调，以能达到最快响应又无超调为最佳参数。

要形象地理解的话，就比如控制水温，要控制现在的水温达到目标的水温，加热的功率根据两者的差距按比例来提供。当当前水温与目标水温差距较小时，就可以以较小的功率加热；当当前水温与目标水温差距较大时，就可以以较大的功率加热；当当前水温与目标水温差距极大时，就可以以极大的功率加热，就可以快速达到接近目标水温的温度。

2.积分（I）部分

控制器的输出与输入误差信号的积分成正比关系，主要用于消除静差。积分作用的强弱取决于积分时间常数 t，t 越大，积分作用越弱，反之则越强。

由于只有比例部分是不可能完全消除静态误差的，加强比例作用只能减小静态误差，所以必须引入积分作用。积分作用消除静差的原理是，只要有误差存在，就对误差进行积分，使输出继续增大或减小，一直到误差为零，积分停止，输出不再变化。但由于实际系统是有惯性的，输出变化后，u(t) 值不会马上变化，须等待一段时间才缓慢变化，因此积分的快慢必须与实际系统的惯性相匹配，惯性大，积分作用就应该弱，积分时间 I 就应该大些，反之而然。如果积分作用太强，积分输出变化过快，就会引起积分过头的现象，产生积分超调和振荡。通常 I 参数也是由大往小调，即积分作用由小往大调，观察系统响应以能达到快速消除误差，达到给定值，又不引起振荡为准。

还是拿控制水温来理解，按前面的按比例提供功率加热，当水温到达某个接近目标水温的温度时，我们按比例提供的加热功率来加入水与水的自然降温速度一样了，诶，温度没法再加了。这时候就需要到积分部分了，在前面一开始加热时就开始累积误差，时刻矫正着加热的力度，从而使水温更加接近目标水温。

3.微分部分

反映偏差信号的变化趋势，并能在偏差信号变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减少调节时间。在微分控制中，控制器的输出与输入误差信号的微分（即误差的变化率）成正比关系。

不论比例调节作用，还是积分调节作用都是建立在产生误差后才进行调节以消除误差，都是事后调节。但是我们肯定是想要我们的系统在控制调整后能快速恢复，比例作用和积分作用是事后调节(即发生误差后才进行调节)，而微分作用则是事前预防控制，即一发现u(t)有变大或变小的趋势，马上就输出一个阻止其变化的控制信号，以防止出现过冲或超调等。D越大，微分作用越强，D越小，微分作用越弱。系统调试时通常把D从小往大调，具体参数由试验决定。

接着用控制水温来理解，就是当我们要对水加热或冷却时，都要一定程度去减小这个水的加热或冷却的速度，从而避免加热或冷却太过了。也许举另一个例子会更加形象，“阻尼” 大家都知道吧，其实微分部分的作用就相当于是 “阻尼” 的作用。

位置式PID

位置式 PID 的公式如下：

下面我们使用代码来实现这条公式。

我们可以先定义一个结构体来保存我们需要使用到的变量。

typedef struct
{
	float target_val;   //目标值
	float err;          //误差值
	float err_last;     //上一个误差值
	float Kp,Ki,Kd;     //比例、积分、微分系数
	float integral;     //积分值
	float output_val;   //输出值
}PID;

然后我们根据公式来写我们的位置式 PID 的运算函数。

float PID_realize(PID* pid, float actual_val)
{
	pid->err = pid->target_val - actual_val;                    (1)
	
	pid->integral += pid->err;                                  (2)

	pid->output_val = pid->Kp * pid->err + 
				     pid->Ki * pid->integral + 
				     pid->Kd * (pid->err - pid->err_last);       (3)

	pid->err_last = pid->err;                                   (4)

	return pid->output_val;
}

（1）首先是计算出误差e(k)，就是用目标值pid.target_val当前值actual_val。

（2）然后就是计算积分部分的误差累加，把每次的误差pid.err累加进pid.integral，就实现了e(k)的积累。

（3）接着就是把三个部分加起来，把计算结果放在pid.output_val里面，最后返回该值即是公式的输出了。

（4）再把这次计算得到的误差e(k)更新为上一次计算得到的误差e(k-1)。

增量式PID

增量式 PID 的公式如下：

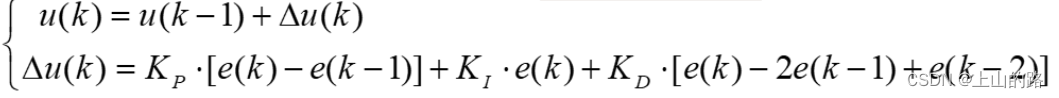
同样，我们可以先定义一个结构体来保存我们需要使用到的变量。，只是与位置式 PID 不同的是这里我们要多一个变量来保存上上次计算得到的误差。

typedef struct
{
	float target_val;   //目标值
	float err;          //误差值
	float err_last;     //上一个误差值
    float err_last_last;//上上个误差值
	float Kp,Ki,Kd;     //比例、积分、微分系数
	float integral;     //积分值
	float output_val;   //输出值
}PID;

下面我们根据公式来写我们的增量式 PID 的运算函数。

float PID_realize(PID* pid, float actual_val)
{
	pid->err = pid->target_val - actual_val;                    (1)
	
	pid->output_val = pid->Kp * (pid->err - pid->err_last) + 
				   pid->Ki * pid->err + 
				   pid->Kd * (pid->err - 2 * pid->err_last + pid->err_last_last);  (2)

    pid->err_last_last = pid->err_last;                         (3)
	pid->err_last = pid->err;

	return pid->output_val;
}

（1）首先是计算出误差e(k)，就是用目标值pid.target_val当前值actual_val。

（2）然后是将三个部分加起来算出Δu(k)，把计算结果放在pid.output_val里面，最后返回该值即是公式的输出了。

（3）再把这次计算得到的误差e(k)更新为上一次计算得到的误差e(k-1)，把上次计算得到的误差e(k-1)更新为上上次计算得到的误差e(k-2)。

注意：这里的函数返回值只是Δu(k)，在函数外还要计算u(k)。

以上就是今天关于 PID 的理论内容了，至于实际操作是需要多去尝试才能掌握到调 PID 参数的技巧以及要掌握的 “度” 。下面是个人找到觉得讲的非常好的B站博主的调参视频连接。

电机速度环和位置环PID调参教程——HZ12I38

下期见！！！