基于PCA和LDA的人脸识别

该项目包含以下内容：

1. 主成分分析PCA方法介绍
2. 使用PCA和LDA进行人脸识别并对比效果
3. 对给定照片进行人脸检测

项目含有方法、流程的介绍，具有可执行的代码以及必要的说明

---

 主成分分析PCA与线性判别分析LDA介绍

        主成分分析（PCA）是一种统计方法，用于降低数据集的维度，同时尽可能保留数据集中的原始信息。它通过正交变换将可能相关的变量转换为一组线性不相关的变量，这些变量被称为主成分。

        主成分分析的步骤：数据标准化：由于 PCA 受到数据尺度的影响，需要先对数据进行标准化处理，确保每个特征的均值为 0，标准差为 1。协方差矩阵计算：计算数据集的协方差矩阵，以确定数据特征之间的相关性。特征值和特征向量计算：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。选择主成分：根据特征值的大小，选择前几个最大的特征值对应的特征向量作为主成分。 转换到新的空间：将原始数据投影到这些主成分上，得到新的数据集，这个新数据集的维度小于原始数据集。

        线性判别分析（Linear Discriminant Analysis，简称 LDA）是一种监督学习的降维技术，它不仅用于降维，还用于分类和特征提取。LDA 的目标是寻找最佳的投影方向，使得不同类别的数据在这个方向上的投影尽可能分开，即类内差异最小化，类间差异最大化。

基于PCA和LDA的人脸识别

数据集

        该数据来自耶鲁大学，包含15个人的165张图片，每个人11张图片。使用 PIL 库读取图片，为了节省计算量，将图片缩小到原来的四分之一，得到每一张图片的尺寸为(97, 115)，我们将其展开为一维向量以作为特征向量，即每张图片 有11155 个特征。

        定义 choose()函数，使用 for 循环遍历 image 列表， 步长为 11（每次迭代处理 11 个连续的图像和标签）。在每次迭代中，使用 image[i:i + 11] 和 label[i:i + 11] 获取一个包含 11 个图像和标签的子集。然后使用 random.sample 函数从子集中随机选择 num 个元素的索引，random.sample 需要从 range(len(data_group)) 中选择，确保索引在有效范围内。再次使用 for 循环遍历 selected_indices，这是一个包含随机选择的索引的列表。 在内部循环中，使用 append 方法将被选中的图像和标签添加到训练集列表 中。使用列表推导式和 extend 方法找到未被选中的图像和标签，并将它们添加 到测试集列表中。函数返回四个 NumPy 数组：train_images、train_labels、 test_images 和 test_labels。 通过这个函数，每次随机选择每个人的N张图片，共计15N张图片作为训 练集，剩下的图片即为测试集。

def load_dataset(folder_path): 
    images = [] 
    labels = [] 
    temp_images = [] 
    for filename in os.listdir(folder_path): 
        image_path = os.path.join(folder_path, filename) 
        label = filename.split('.')[0] 
        image = Image.open(image_path).convert('L') 
        original_size = image.size 
        # 计算新的尺寸，缩小到原来的四分之一 
        new_size = (original_size[0] // 2, original_size[1] // 2) 
        # 缩小图像 
        resampling_filter = Image.Resampling.LANCZOS 
        img_resized = image.resize(new_size, resampling_filter) 
        print(new_size) 
        image_np = np.array(img_resized) 
        # 将图像展平成一维数组 
        image_np = image_np.reshape(image_np.size)  # 将图像展平成一维数组 
        images.append(image_np) 
        labels.append(label) 
return np.array(images), np.array(labels) 
 
def choose(image, label, num): 
    train_labels = [] 
    test_labels = [] 
    train_images = [] 
    test_images = [] 
    for i in range(0, len(image), 11): 
        data_group = image[i:i + 11] 
        labels_group = label[i:i + 11] 
        # 随机挑选5个元素的索引 
        selected_indices = random.sample(range(len(data_group)), num) 
        # 根据索引挑选数据和标签 
        for idx in selected_indices: 
            train_images.append(data_group[idx]) 
            train_labels.append(labels_group[idx]) 
        # 找出未被选中的数据和标签 
        test_images.extend([data for idx, data in enumerate(data_group) if idx not in 
selected_indices]) 
        test_labels.extend([labels_group[idx] for idx in range(len(data_group)) if idx not in 
selected_indices]) 
    return np.array(train_images), np.array(train_labels), np.array(test_images), 
np.array(test_labels)

Eigenfaces和Fisherfaces

        Eigenfaces使用PCA方法进行降维，Fisherfaces使用 LDA方法进行降维，需要样本的 标签。

        通过直接调用sklearn库中的PCA和LinearDiscriminantAnalysis方法来对数据进行降维。然后使用K 最近邻（K-Nearest Neighbors，KNN）算法来进行人脸识别分类。分别对N=5和N=7两种情况进行分析，以错误率作为指标， 每组尝试不同的主成分数进行对比判断，最终确定最好的模型。

KNN实现函数及预测函数：

def classify(images, labels, num_neighbors=3): 
# 使用K近邻分类器 
images_array = np.asarray(images) 
if np.iscomplexobj(images_array): 
images_array = np.real(images_array)  # 取实部 
knn = KNeighborsClassifier(n_neighbors=num_neighbors) 
knn.fit(images_array, labels) 
return knn 
def evaluate_model(knn, images, labels, num_neighbors=3): 
# 预测 
images_array = np.asarray(images) 
if np.iscomplexobj(images_array): 
images_array = np.real(images_array)  # 取实部 
predictions = knn.predict(images_array) 
# 计算误判率 
er = np.sum(predictions != labels) 
return er

训练函数：

def fin(): 
    ferrors = [] 
    images, labels = load_dataset('data2/') 
    print(np.shape(images)) 
    print(np.shape(labels)) 
    scaler = StandardScaler() 
    data_scaled = scaler.fit_transform(images) 
    for i in range(3, 13, 3): 
        errors = [] 
        # 创建LDA对象 
        lda = LinearDiscriminantAnalysis(n_components=i)  # 设置需要保留的主成分数量 
        for j in range(10): 
            train_images, train_labels, test_images, test_labels = choose(data_scaled, labels, 7) 
            print(np.shape(train_images)) 
            print(np.shape(test_images)) 
            # 使用LDA进行降维 
            X_train_lda = lda.fit_transform(train_images, train_labels) 
            X_test_lda = lda.transform(test_images) 
            knn = classify(X_train_lda, train_labels) 
            error = evaluate_model(knn, X_test_lda, test_labels) 
            errors.append(error) 
        errorst = np.mean(errors) 
        ferrors.append(errorst) 
        print(ferrors) 
plot_error_rate(range(3, 16, 3), ferrors) 
ferrors = [] 
    for i in range(10,121,10): 
        errors = [] 
        # 初始化PCA对象，设置保留i个主成分 
        pca = PCA(n_components=i) 
        # 在标准化后的数据上拟合PCA模型并转换数据 
        data_pca = pca.fit_transform(data_scaled) 
        for j in range(10): 
            train_images, train_labels, test_images, test_labels = choose(data_pca, labels, 5) 
            print(np.shape(train_images)) 
            print(np.shape(test_images)) 
            knn = classify(train_images, train_labels) 
            error = evaluate_model(knn, test_images, test_labels) 
            errors.append(error) 
        errorst = np.mean(errors) 
        ferrors.append(errorst) 
        print(ferrors) 
    plot_error_rate(range(10, 121, 10), ferrors)

人脸识别结果

        对于Eigenfaces 方法，以错误率为指标，分别绘制了在 N=3、N=5、N=7 情况下不同主成分数对应的平均错误率的折线图，如下：

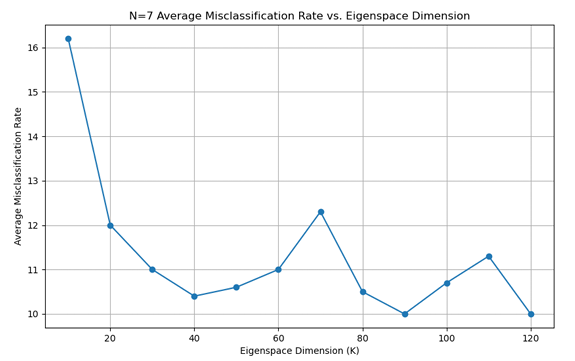
        同样对于Fisherfaces 方法，以错误率为指标，分别绘制了在 N=5 和N=7 情况下不同主成分数对应的错误率的折线图 ，如下：

 

 

        归纳得到： 

        由上可知：在相同的N值下，Fisherfaces方法的性能要高于Eigenfaces方法， 随着选取训练集图片的数目增加，两种模型的性能也随之提高。主成分的数目也 极大的影响了最后的识别效果，对于Eigenfaces方法，当主成分数为30-60时， 错误率较低；对于Fisherfaces 方法，当主成分数为 9-12 时，错误率较低。

        实际上，可绘制出两种降维方法所对应的每种主成分对应的累计方差贡献率折线图。

         从中我们可以看出，对于PCA来说，主成分数目为60时就可以代表95%以 上的数据，同样对于LDA来说，主成分数目为10时就可以代表90%以上的数据。

人脸检测

        对给定的三张图片进行分析，使用矩形框框选出识别到的人脸，旁边的名字表示他与数据集中的哪张人脸最为相近。