极大似然估计
基本思想
极大似然估计是在总体类型已知的条件下使用的一种参数估计方法。
首先是德国数学家高斯在1821年提出的,然而这个方法常归功于英国统计学家费歇。
极大似然法的基本思想通过一个例子说明:
一个猎人和一个二逼外出打猎,一只野兔从前方窜过,一声枪响,野兔应声倒下。如果要你推测,是谁打中的?你会如何想?
选择一个参数使得实验结果有最大的概率
(1)若总体X属离散型,其分布律
P{X=x}=p(x;θ),θ∈Θ
的形式是已知,
θ
为待估参数,
Θ
是
θ
可能取值的范围。
设
X1,X2,⋅⋅⋅,Xn
是来自
X
的样本;则
∏i=1np(xi;θ)
又设 x1,x2,⋅⋅⋅,xn 是 X1,X2,⋅⋅⋅,Xn 的一个样本值;易知样本 X1,X2,⋅⋅⋅,Xn 取 x1,x2,⋅⋅⋅,xn 得概率,为事件 {X1=x1,X2=x2,⋅⋅⋅,Xn=xn} 发生的概率为
L(θ)=L(x1,x2,⋅⋅⋅,xn;θ)=∏i=1np(xi;θ)θ∈Θ
它是 θ 的函数, L(θ) 称为样本的似然函数
由最大似然估计法:固定 x1,x2,⋅⋅⋅,xn ;挑选使得概率 L(θ)=L(x1,x2,⋅⋅⋅,xn;θ) 达到最大的参数
L(x1,x2,⋅⋅⋅,xn;θ)=max L(x1,x2,⋅⋅⋅,xn;θ)
θ 与 x1,x2,⋅⋅⋅,xn 有关,记 θ(x1,x2,⋅⋅⋅,xn) ;称其为参数 θ 的极大似然估计值。
θ(X1,X2,⋅⋅⋅,Xn) 称为参数 θ 的极大似然估计量
求参数的最大似然函数的步骤:
1.写出似然函数
L(θ1,(θ1,⋅⋅⋅,θk)=L(x1,x2,⋅⋅⋅,xn;θ1,⋅⋅⋅,θk)=∏i=1nf(xi;θ1,⋅⋅⋅,θk)
2.取对数
3.将对数似然函数对各参数求偏导数并令其为零,得对数似然方程组。若总体分布中只有一个未知参数,则为一个方程,称对数似然方程
4.从方程组中解出 θ1,⋅⋅⋅,θk ,并记为
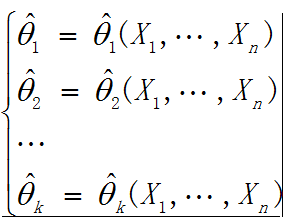
示例



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








