独立性检验的基本思想和初步应用

最新推荐文章于 2024-02-20 00:01:45 发布

宁静致远wyd

最新推荐文章于 2024-02-20 00:01:45 发布

阅读量2.2w

点赞数 8

分类专栏：数学

本文链接：https://blog.csdn.net/weiyudang11/article/details/51555131

版权

数学专栏收录该内容

7 篇文章 0 订阅

订阅专栏

独立性检验的基本思想和初步应用

问题：数学家克里斯提娜每天从一家面包店买一块1000g的面包，并记录下买回的面包的实际质量，一年后这位数学家发现，所记录数据的均值为950个，于是克里斯提娜推断这家秒宝典的面包分量不足。

假设‘面包分量足’，则一年购买面包的质量数据的平均值应当不小于1000个；
“这个平均值不大于950g”是一个与假设“面包分量足”矛盾的小概率事件。
这个小概率事件的发生使庞加莱得出推断结果

假设检验问题的原理

假设检验问题由两个互斥的假设构成，其中一个叫做原假设，用H0表示；另一个叫做备择假设，用H1表示。
例如，在前面的例子中，原假设为： H0：面包份量足，
备择假设为： H1：面包份量不足。
这个假设检验问题可以表达为：

H0：面包份量足 ←→ H1：面包份量不足

求解假设检验问题

在H0成立的条件下，构造与H0矛盾的小概率事件；
如果样本使得这个小概率事件发生，就能以一定把握断言H1成立；否则，断言没有发现样本数据与H0相矛盾的证据。

两种变量

定量变量：体重、身高、体温、考试成绩等
分类变量：性别、是否吸烟、国籍等

研究两个变量的相关关系

定量变量—回归分析（画散点图，相关系数r、相关系数、相关系数 $R^2$ 残差分析）
分类变量 — 独立性检验

为了调查吸烟是否对肺癌有影响，某肿瘤研究所随机地调查了9965人，得到如下结果（单位：人）

不吸烟者中患有肺癌的比重是0.54%
在吸烟者中环肺癌的比重是 2.28%
说明：吸烟者和不吸烟者患肺癌的可能性存在差异，吸烟者患有肺癌的可能性大。

想要知道能够以多大的把握认为“吸烟与患肺癌有关”，
为此先假设
$H_{0}$ :吸烟与患肺癌没关系
用A表示不吸烟，B表示不患肺癌，则“吸烟与患肺癌没有关系”等价于“吸烟与患肺癌独立”，即假设H0等价于 P(AB)=P(A)P(B)

在表中，a恰好为事件AB发生的频数；a+b和a+c恰好分别为事件A和B发生的频数。由于频率接近于概率，所以在H0成立的条件下应该有
$P(A) \approx \frac{a+b}{n},P(B) \approx \frac{a+c}{n},P(AB) \approx \frac{a}{n}$
$\therefore \frac{a}{n}\approx \frac{a+b}{n}*\approx \frac{a+c}{n}$ 其中 $n=a+b+c+d$ 为样本容量， $(a+b+c+d)*a \approx (a+c)*（a+b)$
即： $ad\approx bc$

**因此： $|ad-bc$ 越小，说明吸烟与患肺癌之间关系越弱；
$|ad-bc$ 越大，说明吸烟与患肺癌之间关系越强。**

独立性检验
为了使不同样本容量的数据有统一的评判标准，基于上述分析，我们构造一个随机变量—–卡方统计量
$K^2=\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$
若 $H_0$ 成立，即“吸烟与患肺癌没有关系”，则 $K^2$ 应很小

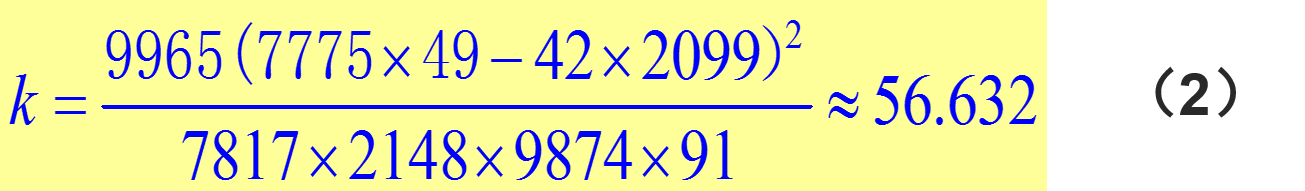
在 $H_0$ 成立的情况下，统计学家估算出如下的概率

$P (K 2 \geq 6.635) \approx 0.01$ $P(K^2 \geq 6.635) \approx0.01$
即在 $H_0$ 成立的情况下， $K^2$ 的值大于6.635的概率非常小，近似于0.01。
也就是说，在 $H_0$ 成立的情况下，对随机变量K2进行多次观测，观测值超过6.635的频率约为0.01。

【总结】独立性检验的解题步骤如下：
第一步　提出假设 $H_0$ ：患肺癌与吸烟没有关系.（目标结论 $H_1$ “患肺癌与吸烟有关系”的反面.）
第二步　计算独立性检验的标准，即统计量 $K^2=n(ad-bc)^2/{(a+b)(c+d)(a+c)(b+d)}$ 的值.（它越小，原假设 $H_0$ 成立的可能性越大；它越大，目标结论H1成立的可能性越大.）
第三步　由独立性检验的临界值表得出结论及其可信度（即在多大程度上适用）

非参数检验

单样本非参数检验是对单个总体的分布形态等进行推断的方法，其中包括卡方检验、二项分布检验、K-S检验以及变量值随机性检验等方法。
总体分布的卡方检验
例如，医学家在研究心脏病人猝死人数与日期的关系时发现：一周之中，星期一心脏病人猝死者较多，其他日子则基本相当。当天的比例近似为2.8：1：1：1：1：1：1。现收集到心脏病人死亡日期的样本数据，推断其总体分布是否与上述理论分布相吻合。
卡方检验方法可以根据样本数据，推断总体分布与期望分布或某一理论分布是否存在显著差异，是一种吻合性检验，通常适于对有多项分类值的总体分布的分析。它的原假设是：样本来自的总体分布与期望分布或某一理论分布无差异。
二项分布检验
在生活中有很多数据的取值是二值的，例如，人群可以分成男性和女性，产品可以分成合格和不合格，学生可以分成三好学生和非三好学生，投掷硬币实验的结果可以分成出现正面和出现反面等。通常将这样的二值分别用1或0表示。如果进行n次相同的实验，则出现两类（1或0）的次数可以用离散型随机变量X来描述。如果随机变量X为1的概率设为P，则随机变量X值为0的概率Q便等于1-P，形成二项分布。
SPSS的二项分布检验正是要通过样本数据检验样本来自的总体是否服从指定的概率为P的二项分布，其原假设是：样本来自的总体与指定的二项分布无显著差异。
从某产品中随机抽取23个样品进行检测并得到检测结果。用1表示一级品，用0表示非一级品。根据抽样结果验证该批产品的一级品率是否为90%。
单样本K-S检验
K-S检验方法能够利用样本数据推断样本来自的总体是否服从某一理论分布，是一种拟合优度的检验方法，适用于探索连续型随机变量的分布。
例如，收集一批周岁儿童身高的数据，需利用样本数据推断周岁儿童总体的身高是否服从正态分布。再例如，利用收集的住房状况调查的样本数据，分析家庭人均住房面积是否服从正态分布。
单样本K-S检验的原假设是：样本来自的总体与指定的理论分布无显著差异，SPSS的理论分布主要包括正态分布、均匀分布、指数分布和泊松分布等。
两独立样本的非参数检验
两独立样本的非参数检验是在对总体分布不甚了解的情况下，通过对两组独立样本的分析来推断样本来自的两个总体的分布等是否存在显著差异的方法。独立样本是指在一个总体中随机抽样对在另一个总体中随机抽样没有影响的情况下所获得的样本。
SPSS中提供了多种两独立样本的非参数检验方法，其中包括曼-惠特尼U检验、K-S检验、W-W游程检验、极端反应检验等。
某工厂用甲乙两种不同的工艺生产同一种产品。如果希望检验两种工艺下产品的使用是否存在显著差异，可从两种工艺生产出的产品中随机抽样，得到各自的使用寿命数据。
甲工艺：675 682 692 679 669 661 693
乙工艺：662 649 672 663 650 651 646 652
曼-惠特尼U检验
两独立样本的曼-惠特尼U检验可用于对两总体分布的比例判断。其原假设：两组独立样本来自的两总体分布无显著差异。曼-惠特尼U检验通过对两组样本平均秩的研究来实现判断。秩简单说就是变量值排序的名次，可以将数据按升序排列，每个变量值都会有一个在整个变量值序列中的位置或名次，这个位置或名次就是变量值的秩。
K-S检验
K-S检验不仅能够检验单个总体是否服从某一理论分布，还能够检验两总体分布是否存在显著差异。其原假设是：两组独立样本来自的两总体的分布无显著差异。
这里是以变量值的秩作为分析对象，而非变量值本身。
游程检验
单样本游程检验是用来检验变量值的出现是否随机，而两独立变量的游程检验则是用来检验两独立样本来自的两总体的分布是否存在显著差异。其原假设是：两组独立样本来自的两总体的分布无显著差异。
两独立样本的游程检验与单样本游程检验的思想基本相同，不同的是计算游程数的方法。两独立样本的游程检验中，游程数依赖于变量的秩。
极端反应检验
极端反应检验从另一个角度检验两独立样本所来自的两总体分布是否存在显著差异。其原假设是：两独立样本来自的两总体的分布无显著差异。
基本思想是：将一组样本作为控制样本，另一组样本作为实验样本。以控制样本作为对照，检验实验样本相对于控制样本是否出现了极端反应。如果实验样本没有出现极端反应，则认为两总体分布无显著差异，相反则认为存在显著差异。
多独立样本的非参数检验
多独立样本的非参数检验是通过分析多组独立样本数据，推断样本来自的多个总体的中位数或分布是否存在显著差异。多组独立样本是指按独立抽样方式获得的多组样本。
SPSS提供的多独立样本非参数检验的方法主要包括中位数检验、Kruskal-Wallis检验、- Jonckheere-Terpstra检验。
例：希望对北京、上海、成都、广州四个城市的周岁儿童的身高进行比较分析。采用独立抽样方式获得四组独立样本。
中位数检验
中位数检验通过对多组独立样本的分析，检验它们来自的总体的中位数是否存在显著差异。其原假设是：多个独立样本来自的多个总体的中位数无显著差异。
基本思想是：如果多个总体的中位数无显著差异，或者说多个总体有共同的中位数，那么这个共同的中位数应在各样本组中均处在中间位置上。于是，每组样本中大于该中位数或小于该中位数的样本数目应大致相同。
Kruskal-Wallis检验
Kruskal-Wallis检验实质是两独立样本的曼-惠特尼U检验在多个样本下的推广，也用于检验多个总体的分布是否存在显著差异。其原假设是：多个独立样本来自的多个总体的分布无显著差异。
基本思想是：首先，将多组样本数据混合并按升序排序，求出各变量值的秩；然后，考察各组秩的均值是否存在显著差异。容易理解：如果各组秩的均值不存在显著差异，则是多组数据充分混合，数值相差不大的结果，可以认为多个总体的分布无显著差异；反之，如果各组秩的均值存在显著差异，则是多组数据无法混合，某些组的数值普遍偏大，另一些组的数值普遍偏小的结果，可以认为多个总体的分布有显著差异。
Jonckheere-Terpstra检验
Jonckheere-Terpstra检验也是用于检验多个独立样本来自的多个总体的分布是否存在显著差异的非参数检验方法，其原假设是：多个独立样本来自的多个总体的分布无显著差异。
基本思想与两独立样本的曼-惠特尼U检验类似，也是计算一组样本的观察值小于其他组样本的观察值的个数
Kendall协同系数检验
它也是一种对多配对样本进行检验的非参数检验方法，与第一种检验方法向结合，可方便地实现对评判者的评判标准是否一致的分析。其原假设是：评判者的评判标准不一致。
有6名歌手参加比赛，4名评委进行评判打分，现在需要根据数据推断这4个评委的评判标准是否一致。（见下页具体分析）
如果将每个被评判者对象的分数看做来自多个总体的配对样本，那么该问题就能够转化为多配对样本的非参数检验问题，仍可采用Friedman检验，于是相应的原假设便转化为：多个配对样本来自的多个总体的分布无显著差异。但对该问题的分析是需要继续延伸的，并非站在对6名歌手的演唱水平是否存在显著差异的角度进行分析，而是在认定他们存在差异的前提下继续判断4个评委的打分标准是否一致。
如果利用Friedman检验出各总体的分布不存在显著差异，即各个歌手的秩不存在显著差异，则意味着评委的打分存在随意性，评分标准不一致。原因在于：如果各个评委的评判标准是一致的，那么对于某个歌手来说将获得一致的分数，也就是说，评委给出的若干个评分的秩应完全相同，这就必然会导致各歌手评分的秩有较大的差异。[1]