标准差分进化（DE）算法笔记丨matlab实现

DE算法matlab代码讲解，：https://www.bilibili.com/video/BV1Ez411b7SJ
评论区有代码分享
一、前言
之前提到过PSO算法，它作为进化算法的入门算法，具有参数少，实现简单，收敛性强的特点。但是，“早熟”这一特点在PSO算法中最为致命，它使得算法极容易陷入局部最优，算法性能也会因此而急剧下降。因此，差分进化算法（DE）应运而生，同样的，DE也是一种基础算法，但是它的多样性更强，不容易出现早熟现象，在一般优化中更加实用。

二、算法流程
1.初始化种群，评价出适应度值，并找出全局最优位置与最优适应度值。
2.进入优化，generation+1。
3.变异。为了保证多样性，变异中需要选择的随机粒子不应与当前更新粒子相同。变异策略通常有以下5种：
变异向量V，F为缩放因子，通常设置为0.5。
(1)DE/rand/1

上式中有三个随机位置，r1,r2,r3是不等于i的不相同的随机数，种群多样性提高，相应的，其收敛性会降低。

(2)DE/best/1

Xbest是种群最优位置，在上式中有着指导作用，能够提升粒子的收敛性。

(3)DE/rand-to-best/1

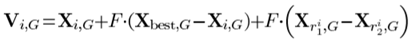
个人认为，上式在多样性和收敛性之间的制衡效果较好。两个随机位置用于开发，最优位置用来指导。它能适用于一般优化问题，但是对于大规模优化这种需要强收敛效果的问题可能不太适用。

(4)DE/best/2

(5)DE/rand/2

上式包含5个不同的随机粒子，种群的开发能力较强，提高了种群多样性。

4.交叉。U为交叉向量，CR是交叉概率。CR的值越大，发生交叉的概率越大，通常CR=0.3。
（1）二项式交叉

      %NP：种群个数；Dim:维度；V：变异向量；U：交叉向量；
        for i=1:NP         
            jRand=randi([1,Dim]);  %jRand∈[1,Dim]
            for j=1:Dim
                k=rand;
                if k<=CR||j==jRand 
                 %j==jRand是为了确保至少有一个U(i,j)=V(i,j)
                    U(i,j)=V(i,j);
                else
                    U(i,j)=X(i,j);
                end     
            end    
        end

（2）指数交叉

       for i=1:NP
            j=randi([1,Dim]);%j∈[1,Dim]
            L=0;
            U(i,:)=X(i,:);
            k=rand;
            while(k<CR && L<Dim)
                U(i,j)=V(i,j);
                j=j+1;
                if(j>Dim)
                    j=1;
                end
                L=L+1;
            end
       end

5.评价进化的新粒子U，适应度值为fitnessU,根据U的适应度值的高低载进行以下筛选。

        if fitnessU(i)<fitnessX(i)
            X(i,:)=U(i,:);
            fitnessX(i)=fitnessU(i);
       end

6.更新最佳位置及适应度值，进入下一代循环stesp2。

三、总结
DE算法的实现比较简单，算法的灵活性较强，不同方法的变异交叉会有不同的实验效果。对于DE算法的改进也非常多，很多改进方法使得其性能突飞猛进，个人认为是一个比较普遍且适应性强的一个基础算法。