ML course_week3

逻辑回归(Logistic Regression)

6.1 分类问题

在分类问题中，要预测的变量 y 是离散的值，因此需要介绍一种 逻辑回归 (Logistic Regression) 的算法。逻辑回归算法是分类算法，我们将它作为分类算法使用，它适用于标签 y 取值离散的情况

分类问题主要用于结果是否属于某一个类（正确或者=错误），比如：判断一封电子邮件是否是垃圾邮件，判断一次金融交易是否欺诈。区分一个肿瘤是恶性的还是良性的

首先讨论二元的分类问题：
将 因变量(dependent variable) 可能属于的两个类别称为负向类 （negative class） 和正向类 （positive class），则因变量 y ∈0，1，其中0表示负向类，1表示正向类

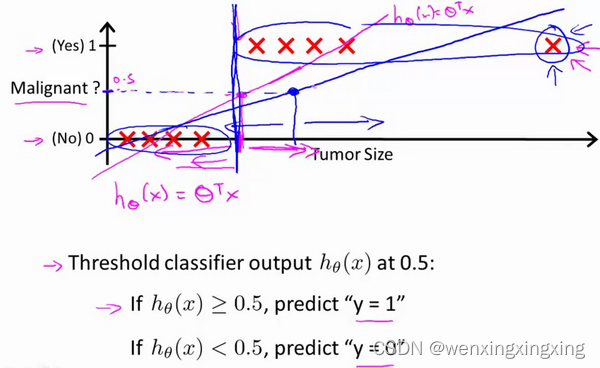
对于分类问题，y取之为0或1，如果使用线性回归算法来解决一个分类问题，假设函数h_θ(x)的输出值可能远大于1，或者远小于0，而所有的训练样本的标签 y 都等于 0 或 1。尽管标签应该取值0或1，但是如果算法的输出值远大于1或者远小于0，就会产生较大的误差，因此需要介绍逻辑回归算法，这个算法可以保证：输出值永远在0~1之间

6.2 假说函数

在分类问题中，要用什么样的函数来表示逻辑回归的假设函数 h_θ(x)。我们希望分类器的输出值在0和1之间，因此，我们希望想出一个满足某个性质的假设函数，这个性质是它的预测值要在0和1之间。

回顾乳腺癌的分类问题，如果使用线性回归的方法求出适合数据的一条直线：

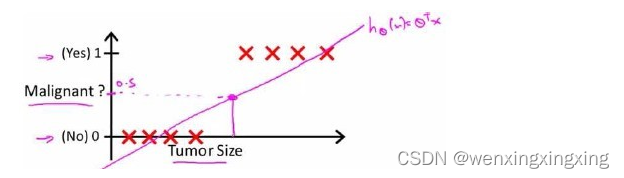
根据线性回归模型我们只能预测连续的值，然而对于分类问题，我们需要输出0或1，我们可以预测：

• 当 h_θ(x) >= 0.5时，预测值 y = 1
• 当 h_θ(x) < 0.5时，预测值 y = 0

对于上图所示的数据，似乎也能够很好的完成分类任务。但假如预测一个非常大尺寸的恶性肿瘤，将其作为实例加入我们的训练集中，将获得一条新的直线。

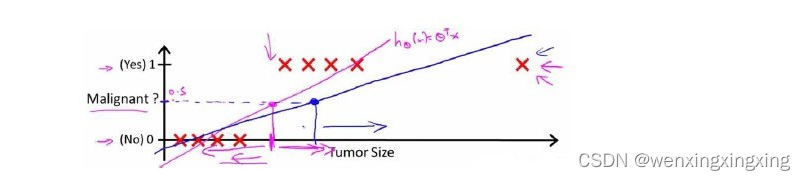
可以看出，线性回归模型，因为其预测的值可以超越[0,1]的范围，并不适合解决这样的问题。

因此有必要引入一个新的模型：逻辑回归。逻辑回归，该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是：
h_θ(x) = g(θ_TX)，其中：X表示特征向量；g代表逻辑函数，公式为：g(z) = 1/(1+e^-z)，是一个常用的S形函数 （Sigmoid function）

python 代码实现：

	import numpy as np
	    
	def sigmoid(z):
	    
	   return 1 / (1 + np.exp(-z))

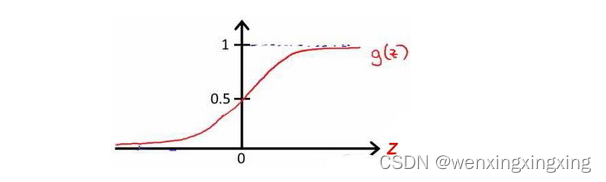
该函数的图像为：

合起来，我们得到逻辑回归模型的假设：
对模型的理解：g(z) = 1/(1+e^-z)
h_θ(x) 的作用是，对于给定的变量，根据选择的参数计算输出变量=1的可能性，即h_θ(x) = P(y = 1 | x; θ)，例如，对于给定的x，计算得出 h_θ(x) = 0.7，则表示70%的几率 y 为正向类，相应的 y为负向类的几率为1-0.7 = 0.3

6.3 决策边界(decision boundary)

回顾逻辑回归的假设函数：

在逻辑回归中，我们预测：
- 当 h_θ(x) >= 0.5时，预测 y = 1
- 当 h_θ(x) < 0.5时，预测 y = 0

根据上面绘制出的S型曲线，我们知道：

• z = 0时，g(z) = 0.5
• z > 0时，g(z) > 0.5
• z < 0时，g(z) < 0.5

又z = θ^Tx，即：

• θ^Tx >= 0，预测 y = 1
• θ^Tx < 0，预测y = 0

现在假设我们有一个模型：

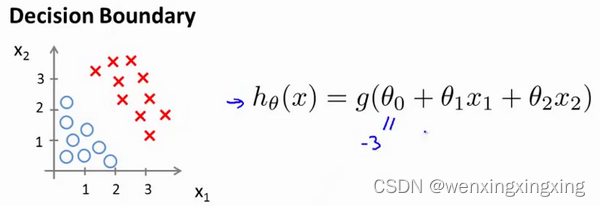
并且参数 θ 是向量[-3 1 1]，则当-3 + x₁ + x₂ >= 0；即 x₁ + x₂ >= 3时，模型预测 y = 1。因此可以绘制x₁ + x₂ = 3这条线便是我们模型的分界线，将预测为1和预测为0的区域分隔开：

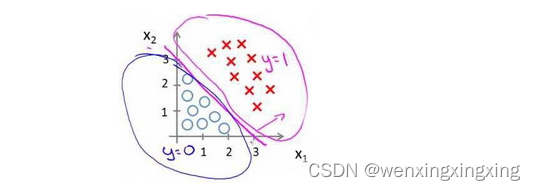
假使我们的数据呈现这样的分布情况，现有的假设函数就很难适用。

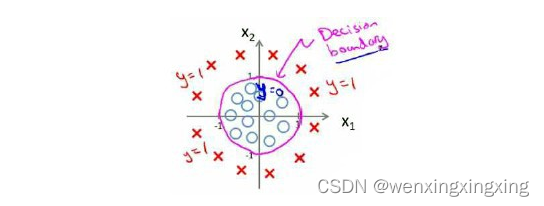
因为需要用曲线才能分隔 y = 0 的区域和 y = 1 的区域，我们需要二次方特征,，其中特征向量是 [-1, 0, 0, 1, 1]，于是得到的判定边界恰好是圆点在原点且半径为1的圆形。

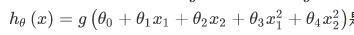
6.4 代价函数

逻辑回归模型的代价函数同样是需要寻找拟合的参数 θ，对于线性回归模型，代价函数的定义是所有模型误差的平方和，理论上讲，逻辑回归模型也可以沿用，但问题在于，当我们将 h_θ(x)= g(z) = 1/(1+e^-z)代入此定义的代价函数后，得到的是一个非凸函数 （non-convexfunction）


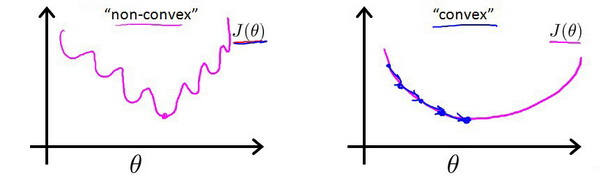
这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值。

线性回归的代价函数为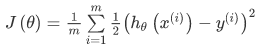：。重新定义逻辑回归的代价函数为：

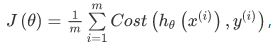
其中：

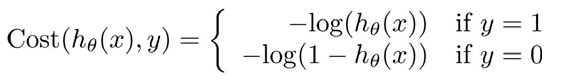
h_θ(x)与Cost( h_θ(x⁽ⁱ⁾), y)之间的关系如下图所示：

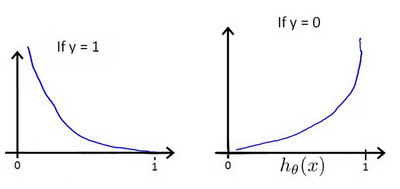
这样构建的Cost( h_θ(x⁽ⁱ⁾), y)函数的特点是：

• 当实际的 y = 1且 h_θ(x⁽ⁱ⁾)也为1时，误差为0；当 y = 1但 h_θ(x⁽ⁱ⁾)不为1时，误差随着 h_θ(x⁽ⁱ⁾)变小而变大
• 当实际的 y = 0 且 h_θ(x⁽ⁱ⁾)也为0时，误差为0；当 y = 0 但 h_θ(x⁽ⁱ⁾)不为0时，误差随着 h_θ(x⁽ⁱ⁾)变大而变大

可以将构建的 Cost( h_θ(x⁽ⁱ⁾), y) 简化如下：

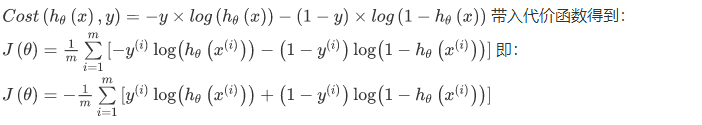
Python 代码实现：

	xxxxxxxxxx
	import numpy as np
	    
	def cost(theta, X, y):
	    
	  theta = np.matrix(theta)
	  X = np.matrix(X)
	  y = np.matrix(y)
	  first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
	  second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
	  return np.sum(first - second) / (len(X))

对此代价函数使用梯度下降法来求得能使代价函数最小的参数。算法为：

求导后得到：

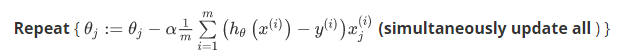
可以证明此代价函数是一个凸优化问题，代价函数 J(θ)是一个凸函数，并且没有局部最优值：
推导过程：

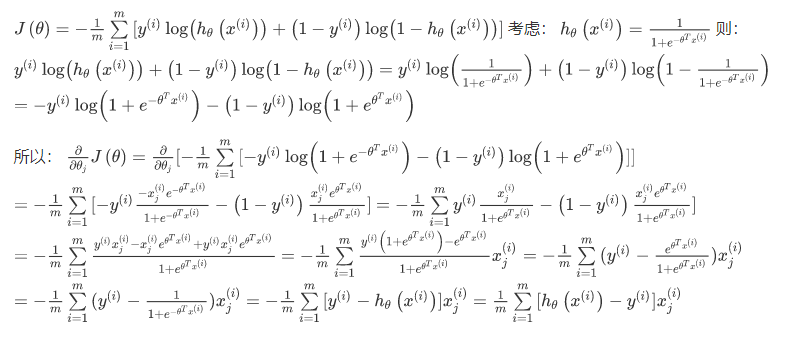
注：虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的 h_θ(x) = g(θ^TX)与线性回归中不同，所以实际上是不一样的。另外，在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。

6.5 简化的代价函数和梯度下降

逻辑回归的代价函数：

这个式子可以合并成：


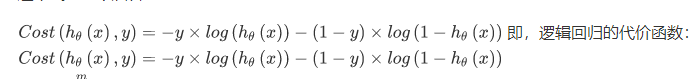
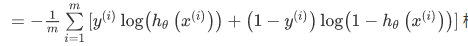
现在就是尽量寻找让 J(θ)取得最小值的参数θ。如果我们给出一个新的样本，假如某个特征 x，我们可以用拟合训练样本的参数θ，来输出对假设的预测。 另外，我们假设的输出，实际上就是这个概率值：p(y = 1 | x; θ)，就是关于x以θ为参数，y=1的概率，也可以认为就是估计y=1的概率。

最小化代价函数的方法，是使用梯度下降法梯度下降法(gradient descent)，通常的梯度下降法的模板：

要反复更新每个参数，用这个式子来更新，就是用它自己减去学习率 α 乘以后面的微分项。求导后得到：

最后得到：

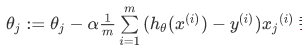
如果有n个特征，参数向量θ包括θ₀，θ₁，θ₂一直到θ_n，那么就需要用上次同时更新所有的θ的值。

逻辑回归的更新规则和线性回归的更新规则是一样的，但是两则的假设函数却不同：
线性回归：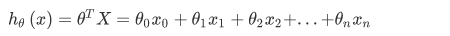
逻辑回归：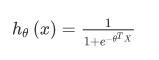
因此，即使更新参数的规则看起来基本相同，但由于假设的定义发生了变化，所以逻辑函数的梯度下降，跟线性回归的梯度下降实际上是两个完全不同的东西。我们可以使用 for循环 来更新参数值，或者 向量化实现，然后对n个参数同时更新

特征缩放也适用于逻辑回归。如果你的特征范围差距很大的话，那么应用特征缩放的方法，同样也可以让逻辑回归中，梯度下降收敛更快。