排序算法通常分为外部排序和内部排序,通常所说的八类排序属于内部排序;
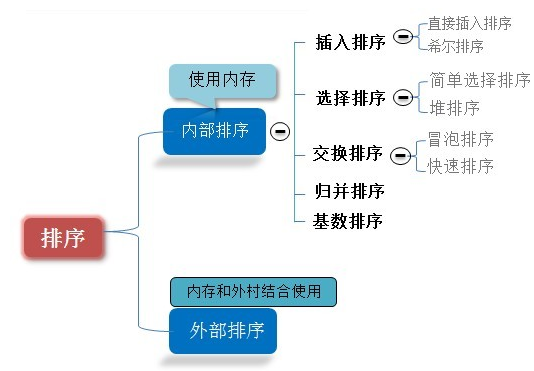
外部排序在此不说明,主要给出八类排序的简单思想和实现:
1.插入排序
1.1 直接插入排序:
每次将一个新数,插入到已经排列好的有序序列当中,新数作为key值和有序序列中的数值比较。
代码实现
#include <stdio.h>
void main(){
int i,j,key;
int A[7]={12,41,23,17,5,2,38};
for(j=1;j<7;j++){
key=A[j];
for(i=j-1;i>=0;i--){
if(A[i]>key){
A[i+1]=A[i];
}else{
break;
}
}
A[i+1]=key;
}
for(i=0;i<7;i++){
printf("%d-",A[i]);
}
}1.2希尔排序
希尔排序是1959 年由D.L.Shell 提出来的,相对直接排序有较大的改进。希尔排序又叫缩小增量排序;思想是将待排序的序列分成若干子序列,对每个子序列进行直接插入排序,当序列基本有序时,最后再进行一次直接插入排序;增量d取值:d = {n/2 ,n/4, n/8 …..1}
代码实现:
#include <stdio.h>
#include <iostream>
using namespace std;
void shellInsert(int a[],int n,int dk){
for(int i=dk;i<n;i++){
if(a[i]<a[i-dk]){
int key = a[i];
//cout<<key;
int j=i-dk;
//a[i]=a[j];
while(key<a[j] && j >=0 ){
a[j+dk]=a[j];
j-=dk;
}
a[j+dk]=key;
}
}
}
void shellSort(int a[],int n){
int dk = n/2;
// cout << dk;
while (dk >= 1){
cout <<"dk:"<<dk<<"\n";
shellInsert(a,n,dk);
dk=dk/2;
}
for (int i=0;i<n;i++){
cout << a[i]<<",";
}
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
shellSort(a,13);
return 0;
}
2 选择排序
2.1 简单选择排序
在要排序的一组数中,选出最小(或者最大)的一个数与第1个位置的数交换;然后在剩下的数当中再找最小(或者最大)的
与第2个位置的数交换,依次类推,直到第n-1个元素(倒数第二个数)和第n个元素(最后一个数)比较为止。
代码实现:
#include <iostream>
using namespace std;
int selectMiniKey(int a[],int n,int b){
int min=b;
for (int j=b+1;j<n;++j){
if(a[j]<a[min]){
min=j;
}
}
return min;
}
void selectSort(int a[],int n){
int min,temp;
for(int i=0;i<n;++i){
min=selectMiniKey(a,n,i);
if(i!=min){
temp=a[i];
a[i]=a[min];
a[min]=temp;
}
}
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
selectSort(a,13);
for(int i=0;i<13;++i){
cout << a[i]<<",";
}
return 1;
}
简单选择排序的改进--二元选择排序
每次同时挑选出最小的和最大的:
代码实现:
#include <iostream>
using namespace std;
void selectSort2(int a[],int n){
int min,max,temp;
for(int i=1;i<=n/2;i++){
min=i-1,max=i-1;
for (int j=i;j<=n-i;j++){
if(a[j]>=a[max]){
max=j;
continue;
}
if(a[j]<=a[min]){
min=j;
}
}
cout<<a[min]<<":"<<a[max]<<"\n";
/*
**watch out the swap order,it matters if i-1==max,then the min swap will have effect on max swap
*/
if((i-1)!=max){
temp=a[i-1];a[i-1]=a[min];a[min]=temp;
temp=a[n-i];a[n-i]=a[max];a[max]=temp;
}else{
temp=a[n-i];a[n-i]=a[max];a[max]=temp;
temp=a[i-1];a[i-1]=a[min];a[min]=temp;
}
//temp=a[n-i];a[n-i]=a[max];a[max]=temp;
cout<<i<<":";
for(int z=0;z<n;++z)
cout<<a[z]<<",";
cout << "\n";
}
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
selectSort2(a,13);
for(int i=0;i<13;++i){
cout << a[i]<<",";
}
return 1;
}2.2 堆排序
首先将待排序的序列构建成一个大顶堆或者小顶堆;之后将堆顶元素与最后一个元素交换,选择出最大或者最小的元素;之后将前面n-1个元素重新调整为一个大顶堆或者小顶堆,重复上面的过程,直到选择出最后一个元素;堆排序的过程其实就分为两步:一是构建堆;二是调整堆,事实上构建堆的过程也是通过调整堆来实现的。
代码实现:(递归实现)
#include<iostream>
using namespace std;
void printHeap(int a[],int n){
for(int i=0;i<n;++i)
cout<<a[i]<<",";
cout<<"\n";
}
void heapAdjust(int a[],int s,int e){
int tmp=a[s];
int child=2*s+1;
if(child>=e) return;
if(child+1<e && a[child]<a[child+1]){
++child;
}
if(a[s]<a[child]){
a[s]=a[child];a[child]=tmp;
heapAdjust(a,child,e);
}
}
void heapBuild(int a[],int n){
for(int i=(n-1)/2;i>=0;--i){
heapAdjust(a,i,n);
}
}
void heapSort(int a[],int n){
heapBuild(a,n);
printHeap(a,n);
for(int i=n-1;i>=0;--i){
int tmp=a[0];a[0]=a[i];a[i]=tmp;
heapAdjust(a,0,i);
}
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
heapSort(a,13);
printHeap(a,13);
return 1;
}
3 交换排序
3.1 冒泡排序
在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
代码实现:
#include<iostream>
using namespace std;
void printArray(int a[],int n){
for(int i=0;i<n;++i)
cout<<a[i]<<",";
cout<<"\n";
}
void bubleSort(int a[],int n){
for (int i=0;i<n;++i){
for(int j=0;j<n-i;++j){
if(a[j]>a[j+1]){
int tmp=a[j];
a[j]=a[j+1];
a[j+1]=tmp;
}
}
}
printArray(a,n);
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
bubleSort(a,13);
return 1;
}
3.2快速排序
思想:选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟排序讲待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素值小,另一部分记录的元素值比基准值大,此时基准元素在其排好序后的正确位置;然后分别对这两部分记录用同样的方法继续进行排序,直到整个序列有序。
代码实现:
#include<iostream>
using namespace std;
void printArray(int a[],int n){
for (int i=0;i<n;++i)
cout<<a[i]<<",";
cout << "\n";
}
void swap(int *a,int *b){
int tmp=*a;
*a=*b;
*b=tmp;
}
int partitionKey(int a[],int low,int high){
int key=a[low];
while(low<high){
/*
*whatch the if condition is >= and --high not high--
*/
while(low<high && a[high]>=key)--high;
swap(&a[low],&a[high]);
while(low<high && a[low]<=key) ++low;
swap(&a[low],&a[high]);
}
return low;
}
void quickSort(int a[],int low,int high){
if(low<high){
int key=partitionKey(a,low,high);
/*
*watch that edge number dose not contain key itself
*/
quickSort(a,low,key-1);
quickSort(a,key+1,high);
}
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
quickSort(a,0,12);
printArray(a,13);
return 1;
}
4 归并排序
思想:将两个有序表归并成一个有序表;注意是两个有序表;对于一个待排序列来说,可以将代排序列分成若干个子序列,调整子序列有序后,再将子序列归并成一个更大的有序列,直到序列全部有序。
代码实现
#include<iostream>
using namespace std;
void printArray(int a[],int n){
for(int i=0;i<n;++i)
cout<<a[i]<<",";
cout<<"\n";
}
void merge(int a[],int b[],int first,int mid,int last){
int k=0,i=first,j=mid+1,n=last,m=mid;
while(i<=m && j<=n){
if(a[i]<a[j]){
b[k++]=a[i++];
}else{
b[k++]=a[j++];
}
}
while(i<=m) b[k++]=a[i++];
while(j<=n) b[k++]=a[j++];
for(int s=0;s<k;s++){
a[s+first]=b[s];
}
}
void mergeSort(int a[],int b[],int s,int e){
int mid;
if(s==e) return;
mid=(s+e)/2;
mergeSort(a,b,s,mid);
}
void mergeSortRecursive(int a[],int n){
int *p = new int[n];
if(p==NULL) return;
mergeSort(a,p,0,n-1);
printArray(a,n);
}
int main(){
int a[13]={12,45,67,8,90,34,25,67,9,10,14,78,29};
mergeSortRecursive(a,13);
return 1;
}
5 基数排序
比较简单,就不实现了,感兴趣的可以看一下http://blog.csdn.net/hguisu/article/details/7776068这篇博客,讲的比较细.






















 882
882

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








