逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,使得逻辑回归模型成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。本文主要详述逻辑回归模型的基础,至于逻辑回归模型的优化、逻辑回归与计算广告学等,请关注后续文章。
1 逻辑回归模型
回归是一种极易理解的模型,就相当于y=f(x),表明自变量x与因变量y的关系。最常见问题有如医生治病时的望、闻、问、切,之后判定病人是否生病或生了什么病,其中的望闻问切就是获取自变量x,即特征数据,判断是否生病就相当于获取因变量y,即预测分类。
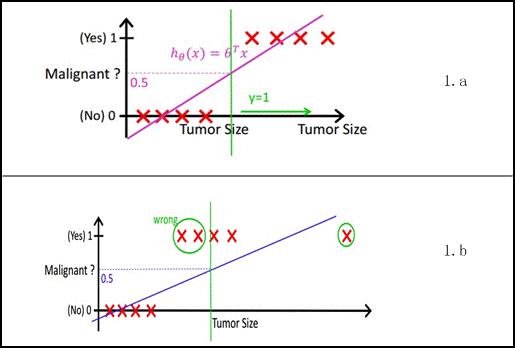
最简单的回归是线性回归,在此借用Andrew NG的讲义,有如图1.a所示,X为数据点——肿瘤的大小,Y为观测值——是否是恶性肿瘤。通过构建线性回归模型,如hθ(x)所示,构建线性回归模型后,即可以根据肿瘤大小,预测是否为恶性肿瘤hθ(x)≥.05为恶性,hθ(x)<0.5为良性。
图1 线性回归示例
然而线性回归的鲁棒性很差,例如在图1.b的数据集上建立回归,因最右边噪点的存在,使回归模型在训练集上表现都很差。这主要是由于线性回归在整个实数域内敏感度一致,而分类范围,需要在[0,1]。逻辑回归就是一种减小预测范围,将预测值限定为[0,1]间的一种回归模型,其回归方程与回归曲线如图2所示。逻辑曲线在z=0时,十分敏感,在z>>0或z<<0处,都不敏感,将预测值限定为(0,1)。
图2 逻辑方程与逻辑曲线
逻辑回归其实仅为在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,逻辑回归成为了机器学习领域一颗耀眼的明星,更是计算广告学的核心。对于多元逻辑回归,可用如下公式似合分类,其中公式(4)的变换,将在逻辑回归模型参数估计时,化简公式带来很多益处,y={0,1}为分类结果。
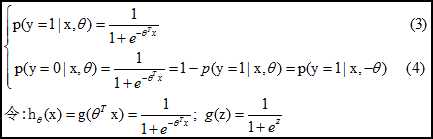
对于训练数据集,特征数据x={x1, x2, … , xm}和对应的分类数据y={y1, y2, … , ym}。构建逻辑回归模型f(θ),最典型的构建方法便是应用极大似然估计。首先,对于单个样本,其后验概率为:
那么,极大似然函数为:
log似然是:
2 梯度下降
由第1节可知,求逻辑回归模型f(θ),等价于:
采用梯度下降法:
从而迭代θ至收敛即可:









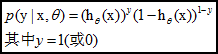
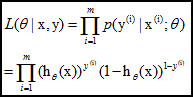

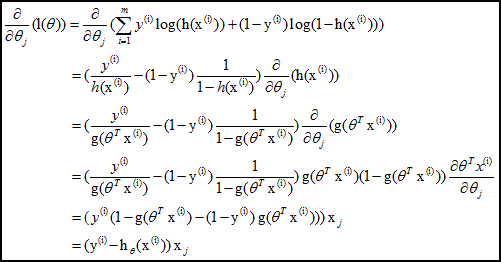














 7014
7014











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








