量子支持向量机

支持向量机，俗称SVM，是广泛使用的监督机器学习算法技术之一。 SVM 尝试在输入特征空间中找到分隔两个类的超平面。 有时，在给定的输入空间中找到一个好的超平面可能不是最佳的。 通过使用各种核方法，我们可以目标是在高维输入特征空间中找到超平面，而无需显式定义高维特征空间。 核定义了高维特征向量空间中给定输入特征向量的点积。 由于寻找超平面的解决方案取决于输入特征向量的点积，而不是明确地取决于输入特征，因此支持向量机可以很好地与不同的内核配合使用，以呈现决策边界中相对于输入特征的非线性。 简而言之，内核帮助将输入特征空间中的向量投影到更高维的向量空间，在该空间中可以获得线性决策边界来分离两个类。 根据 SVM 公式中使用的核函数，学习超平面的优化目标可以是凸的或非凸的。 非凸优化可能会导致解决方案收敛于局部最小值，从而导致性能不佳。 对此，我们可以使用 Grover 算法的量子最小化子程序来求解非凸优化问题的全局最小值。 参见图 5-5。

假设我们的超平面方向由垂直于超平面的参数向量和定义超平面与原点距离的偏差 b 定义，则可以定义位于超平面上的特征向量如下：

在 SVM 中，我们尝试以某种方式构建超平面，使得一类数据点（例如标签 y = 1）满足以下关系：

具有标签 y = − 1 的另一类数据点应满足以下关系：

正如我们所看到的，我们并不满足于让超平面分隔两个类，而是希望通过定义另外两个由给出的超平面来在两个类之间进行一些额外的分隔。

在 SVM 中，我们想要选择模型的参数，使得由超平面定义的两个类边界之间的距离最大化。 我们取两个点，位于超平面上，属于类别 1，点位于超平面上，属于类别 -1。 由于这些点位于超平面上，因此它们满足以下条件：

可以将公式 5-74 中的两个公式相减，得到以下结果：

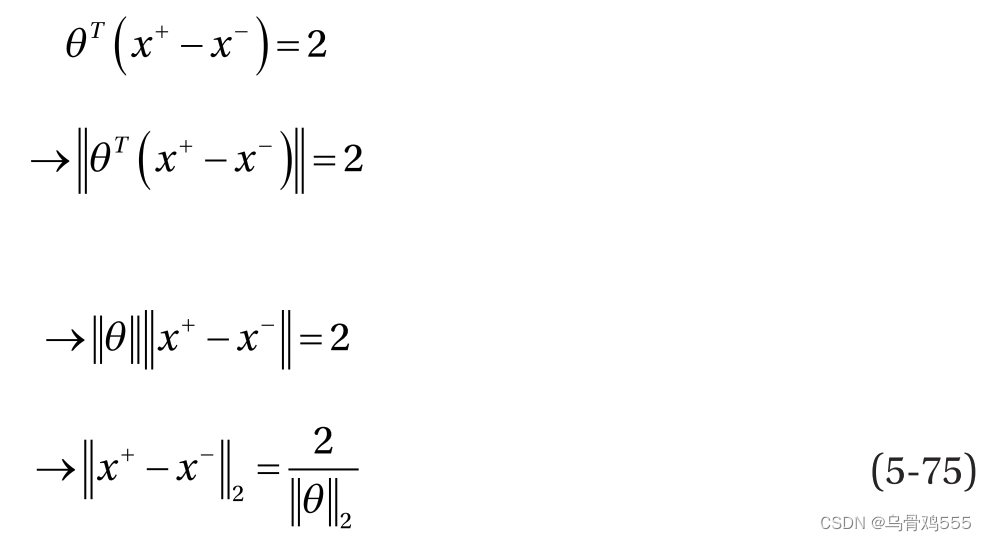
两个超平面之间的距离就是两个点和之间的距离。

为了学习SVM超平面的参数，我们最大化了超平面之间的距离，使得类之间的距离尽可能的远。最大化超平面之间的距离类似于最小化参数θ的范数，如公式5-75所示。然而，在没有任何约束的情况下无限地最大化分离会导致错误分类。为了确保数据点被正确分类，我们需要对每个数据点遵守式5-72和式5-73的约束，总结如下:

因此，优化问题可以写成:

它受到以下约束: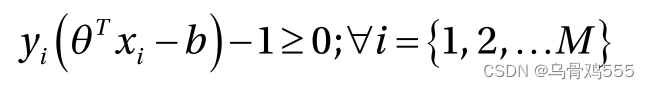

由于这是一个约束优化问题，我们可以使用拉格朗日乘子和Karush-Kuhn-Tucker条件来解决问题。对于大小为M的训练数据集中的每个数据点，使用拉格朗日乘子，总体目标函数可表示为:

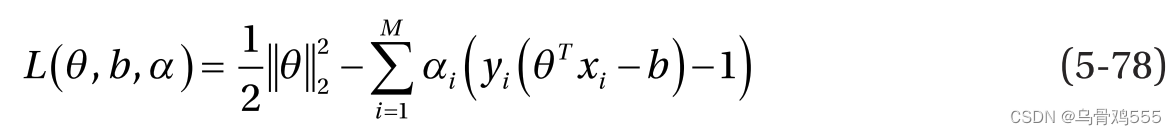
拉格朗日乘子决定支持向量机的支持向量。不为零的数据点只影响模型预测，称为支持向量。的数据点不影响模型参数，因此不影响预测。

在前面的表达式中，α是所有M个数据点的拉格朗日乘子向量。通过式5-78中目标的最小最大优化，可得到优化后的参数θ∗，b∗，α∗: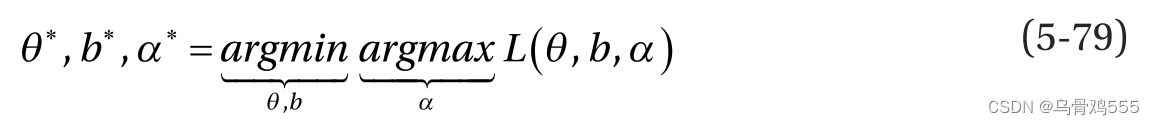

我们通常分两步进行优化。首先，我们最小化关于θ和b的目标，并代入公式5-79中推导出的θ和b的值。为了做到这一点，我们取L(θ， b， α)对θ和b的梯度，并设它为零。物镜相对于θ的梯度得到如下:

同理，令objective对b求导为零，得到:

将式5-80中θ的值代入，得到: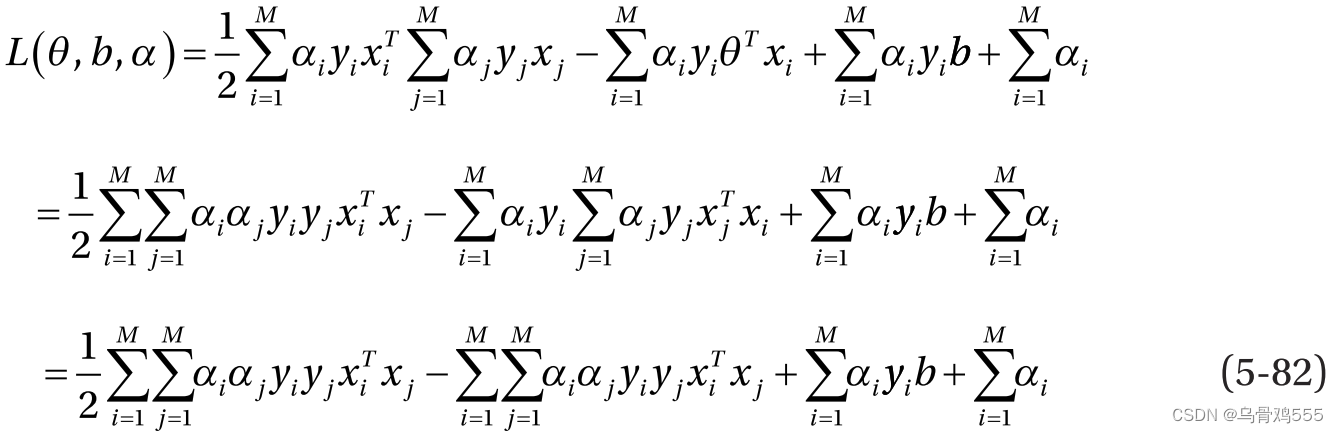

根据公式5-81，公式5-82中的第三项为零，因此我们可以将目标简化为: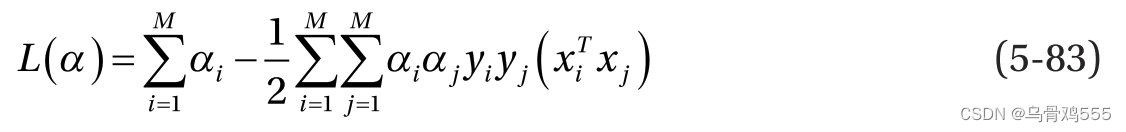

现在我们的目标完全是拉格朗日乘子αi，因此我们进入了优化的第二阶段我们需要解决对偶优化问题，定义如下: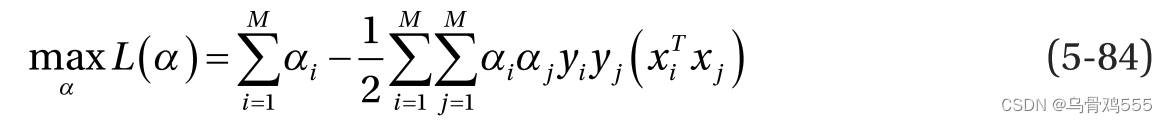

它受到以下限制: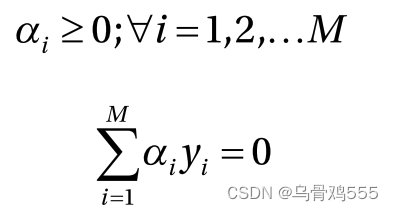

如公式5-84所示，对偶公式只包含特征向量之间的点积，因此我们可以用核函数代替点积来学习非线性决策边界。这是因为两个特征向量之间的核函数是在更高的维度上定义它们的点积。例如，两个特征向量和之间的高斯核定义如下:

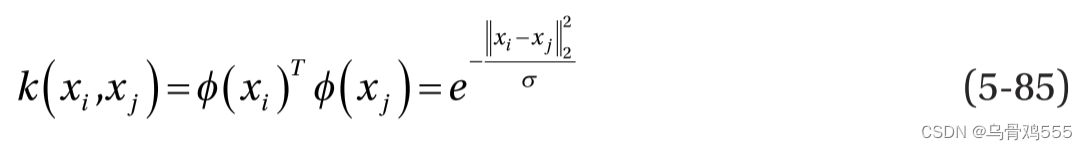
公式 5-85 中的函数将特征向量投影到更高的维度，但我们不需要学习它。 从对偶公式中可以看出，我们只对点积感兴趣，而核 k(., .) 提供了相同的点积，而无需显式学习。 然而，向更高维度的投影的性质将由所选的内核来定义，因此根据问题，可能需要选择最佳的内核。 因此，一般来说，对偶公式中的目标可以用核函数重写如下：

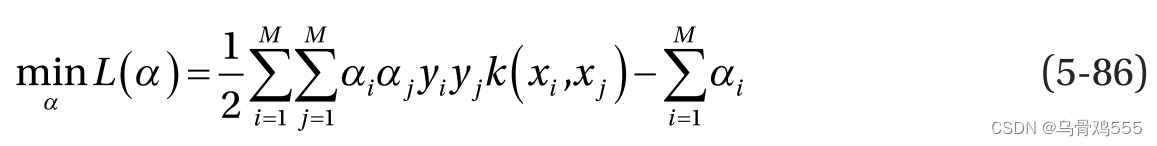
请注意，在公式 5-86 中，我们通过将目标乘以 -1，将最大化问题更改为最小化问题。

需要注意的一件事是，二元类分类过程中的决策函数并不那么严格，我们让超平面 代替超平面进行类别区分。 因此，决策函数可以写成如下：

从公式 5-80 中，我们有。 将其代入公式 5-87，我们得到更新的决策边界，如下所示：

与训练目标非常相似，预测的决策边界取决于预测数据点 x 和训练中的数据点的点积。 因此，我们可以通过用核函数替换点积来概括决策边界，如下所示：

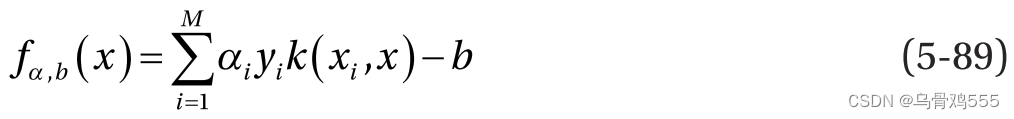
Anquita 等人的量子 SVM 版本。 通过尝试离散解来解决这个对偶公式，其中拉格朗日乘数被假定为 0 或 1。这很容易允许拉格朗日乘数向量表示为 M 量子位的基本状态 |α〉 = ∣ α1 α2…αM〉 系统。 M 量子位系统将有个基本状态，它们为优化问题提供了详尽的拉格朗日乘子向量集可能性。 这个想法是解决使用 Grover 优化算法找到最优拉格朗日乘子向量 |α*〉 的对偶问题。

执行函数 L(α) 并输出 1 以获得最佳 α* 的预言机 O 需要作为该量子 SVM 公式的一部分来实现。 Grover 算法的输入是所有可能的拉格朗日乘子的等叠加，期望的输出是高概率的最优拉格朗日乘子∣α*〉。

Grover 算法为公式 5-64 中的目标函数提供了全局最优值，并将时间复杂度从 O(N) 降低到。 然而，实现这样的量子 SVM 算法确实有其自身的局限性。 请注意，构建一个实现具有复杂内核的目标函数 L(α) 的预言机可能是一项非常具有挑战性的任务。

量子最小二乘支持向量机

正如我们所讨论的，Anquita 等人提出的量子 SVM 提案。 由于设计返回最佳拉格朗日乘数向量的量子预言机的复杂性，这可能不是实现 SVM 的实用方法。 一种称为最小二乘 SVM 的不同公式可以避免构建量子预言机，因此作为量子机器学习范式中选择的 SVM 公式而广受欢迎。量子最小二乘SVM算法称为qSVM，它使用前面讨论的Harrow、Hassidim和Lloyd的HHL算法来确定模型的参数。

最小二乘 SVM 公式使用与对偶公式不同的方法，通过为每个数据引入误差松弛项，将每个数据点的不等式约束转换为等式约束点，如下所示：

作为优化的一部分，我们最小化每个数据点的误差平方和作为正则化器，以及与最大化超平面之间的距离相关的代价目标。对于每个数据点，优化问题也应遵守式5-90中的等式约束。最小二乘支持向量机的总体目标为:
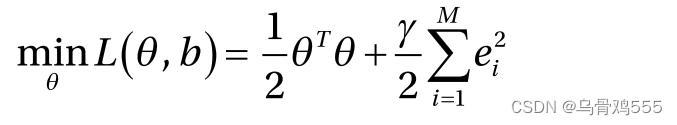
它受以下约束: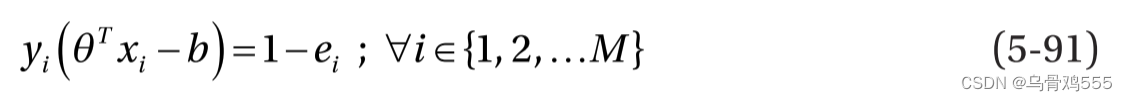

在SVM中，二元类被标记为+1或- 1，因此。在方程5-91的等式两边乘以，我们得到:

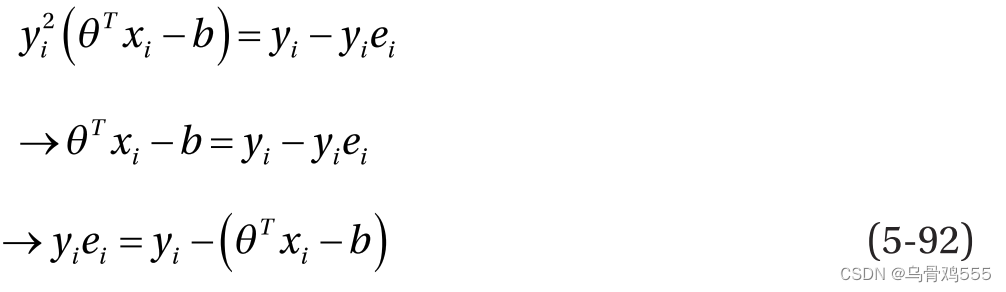
因为对于SVM, yi∈{−1，+1}，所以对于正类，为+ei，对于负类，为- ei。一般来说，我们可以放宽ei≥0的约束，用ei代替，使得。这允许我们重写公式5-92如下:

因此，最小二乘支持向量机的总体目标可以写成: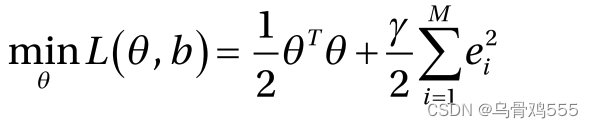

它受到以下约束: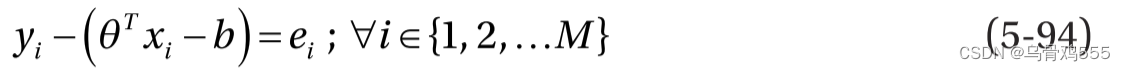

每个数据点(xi, yi)的约束可以使用拉格朗日乘子αi在现有目标中组合，如下所示:

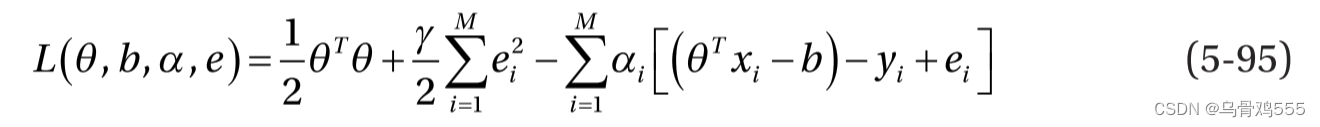
最优条件如下: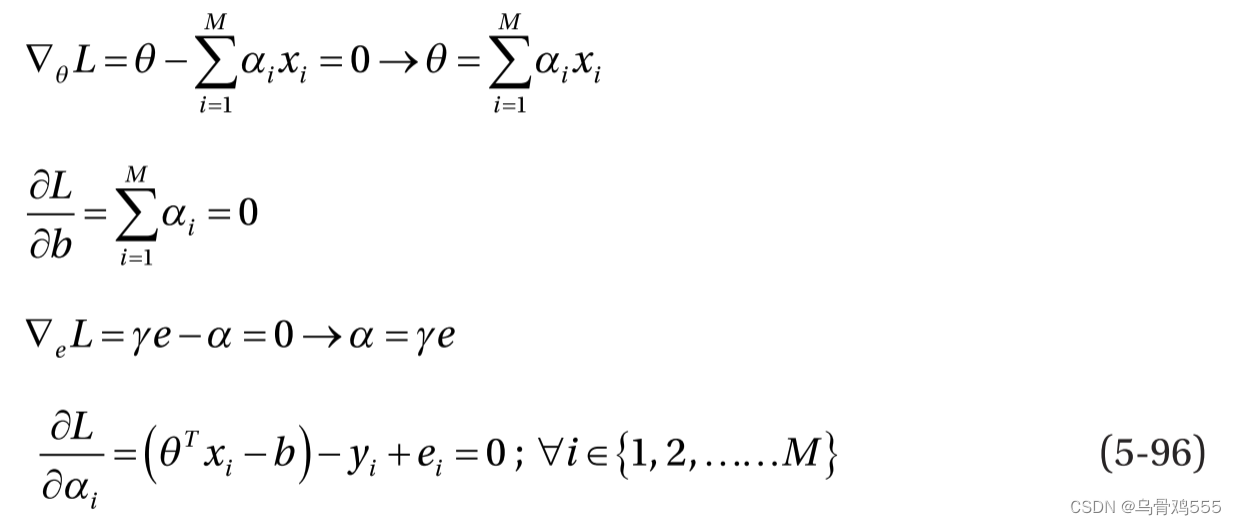

通过求解与最优性有关的前四组方程(见式5-96)，我们可以去掉θ和误差松弛项ei。这样我们就得到了一个线性方程组，表示如下:

式5-97中，K为维数为M × M的核矩阵，Y为列矩阵中所有M个数据点的目标标签向量yi。广义核矩阵项为k(xi, xj)，其中i和j是矩阵k的行数和列数。我们可以求解式5-73所示方程组，使用HHL算法推导出α和b。分类的决定边界将继续如下: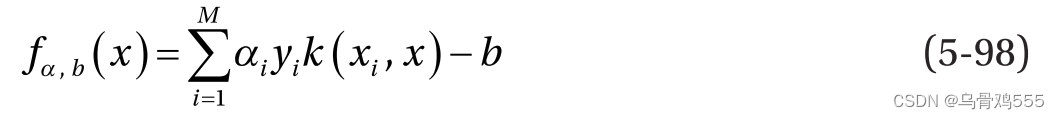

使用Qiskit实现SVM

在本节中，我们将执行IBM Qiskit中的量子支持向量机实现，并查看它在乳腺癌数据集分类任务中的表现。对于此任务，我们首先对给定数据进行标准Z缩放，然后执行主成分分析以将数据维数降至2。这将允许我们使用两个量子位来表示数据。Qiskit还提供了一种高维投影数据的方法。我们使用Qiskit的SecondOrderExpansion功能来创建二阶特性。在创建SecondOrderExpansion特性时，entangler_map允许您在特性之间创建交互。将二阶特征数据点输入到QSVM例程中训练模型。
github去找。