字符串算法总结

最新推荐文章于 2024-05-03 19:07:10 发布

wh653

最新推荐文章于 2024-05-03 19:07:10 发布

阅读量598

点赞数 1

分类专栏： ACM/ICPC之路文章标签：字符串数据结构

本文链接：https://blog.csdn.net/wh653/article/details/46858049

版权

ACM/ICPC之路专栏收录该内容

20 篇文章 0 订阅

订阅专栏

集训刚开始几天学了一下字符串算法(只看了一点点), 不过今天开始要看一些数学计算几何方面的东西, 所以先写个总结, 以后回来继续看.

暂时给出kmp以及一些练习题, AC自动机和hash后续给出

主要介绍:
0. Trie树
1. kmp算法
2. AC自动机 (待填坑)
3. 字符串哈希 (待填坑)

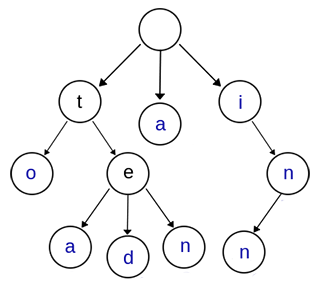
Trie树

又叫字典树, 其实这个数据结构还是比较直观的, 比如所有字符串都是26个字母的, 那么这个字典树就是一个26叉树, 如果abcd存在, 那么字典树里就有root -> a -> b -> c -> d的一条路.
请允许我盗图..

#include <cstdio>
#include <cstring>
using namespace std;
const int segma_size = 26;
const int maxsize = 50000;
struct TrieNode{
    int val;
    int cnt;
    int next[segma_size];
    TrieNode(){
        memset(next, 0, sizeof(next));
        cnt=0;
    }
};
TrieNode trie[maxsize];
int tcnt;
void init()
{
    tcnt = 1;
}
void insert(char *key)
{
    char *p = key;
    int u = 0;
    while(*p)
    {
        if(trie[u].next[*p-'a'] == 0)
            trie[u].next[*p-'a'] = tcnt++;
        u = trie[u].next[*p-'a'];
        p++;
    }
    trie[u].cnt = 1;
}
int find(char *key)
{
    char *p = key;
    int u = 0;
    while(*p)
    {
        if(trie[u].next[*p-'a'] == 0)
            return 0;
        u = trie[u].next[*p-'a'];
        p++;
    }
    return trie[u].cnt;
}

这是我写的一个静态的Trie树, 不要用new, delete来做..太慢

kmp算法

kmp算法是用于处理两个字符串匹配的算法, 有一个较长的文本串S(长度n), 模式串P(长度m), 在S中查找P是否出现过, 暴力算法为O(n*m).

KMP算法是一个比较晦涩的算法, 但是可以做到O(n+m)的复杂度

大意是计算出模式串的Next数组.在暴力匹配的时候, i指针在文本串上向后滑动, j指针在模式串上向后滑动, 如果匹配失败, 则i回滚到模式串的开头后一个位置继续开始匹配, 即 每次与模式串匹配失败, i向前回滚, 因此最坏情况下, 每次都回滚m个位子, 总共n次, 复杂度为O(m*n)

而求出Next数组后, i指针不前移, 利用Next数组将模式串跳转,

例如模式串是abcdabce, 匹配abcdabc都成功, 然而匹配e的时候发现, 跟文本串(例如abcdabcfabc)的f不一样, 此时, abcdabce中, e前面的abc和文本串f前面的abc相同, 而e前面的abc和模式串开头的abc也相同, 那么只需要从d开始与文本串匹配即可. (前面已经一样, 不用比较了)

给一个非常详细的帖子, 从头到尾理解KMP
或者可以看看hihocoder里的KMP算法那个, 也不错

这里也有一个帖是介绍了比较多的好的题目的KMP练习题

求Next数组的一个模板, kmp匹配就不写了, 并不是所有时候都需要匹配..Next数组灵活使用比较蛋疼..

#include <cstdio>
#include <cstring>
using namespace std;
const int maxsize = 200050;
int _next[maxsize];
void getNext(char *p)
{
    int pLen = strlen(p);
    int i, k;
    _next[0] = -1;
    for(i=1; i<=pLen; i++)
    {
        k = _next[i-1];
        while(k>=0 && p[k] != p[i-1])
            k = _next[k];
        _next[i] = k+1;
    }
}