数据结构的终极boss：AVL树的详细讲解及代码实现

1.为什么要引入AVL树

1.当插入数据有规律时，就会出现歪脖子树，也就是整颗二叉树像一根棍一样的情况，使搜索的时间复杂度退化到O(n)，为了解决这个问题，我们引入了AVL树

2.AVL的存储结构：五元组

template <class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K,T>* left;
	AVLTreeNode<K, T>* right;
	AVLTreeNode<K, T>* _parent;
	pair<K, T>kv;
	int bf;
};

avl树作为二叉树的改良形式，是可以由avl树写出map等容器的（原版红黑树），所以它存储的数据为KV模型，除了传统二叉树的数据，左节点，右节点外，它还有指向父亲的节点的指针以及平衡因子，这个平衡因子的初始值为0，当此节点有左节点时，平衡因子加一，有右节点时，平衡因子减一

3.插入函数

bool insert(const pair&(K,V)
{
	if (root == nullptr)
	{
		root = new Node(kv);
		return true;
	}
	else
	{
		Node* parent = nullptr;
		Node* cur = root;
		while (cur)
		{
			if (cur->kv.first > key)
			{
				parent = cur;
				cur = cur->left;
			}
			else if (cur->kv.first < key)
			{
				parent = cur;
				cur = cur->right;
			}
			else
			{
				return false;
			}

		}
		cur = new Node(key);
		if (parent->kv.first < key)
		{
			parent->right = cur;
			cur->_parent = parent;
		}
		else
		{
			parent->left = cur;
			cur->_parent = parent;
		}
		
	}
	while (parent)
	{
		if (cur == parent->left)
		{
			parent->bf--;
		}
		else
		{
			parent->bf++;
		}
		if (parent->bf == 0)
		{
			break;
		}
		else if (parent->bf == 1 || parent->bf == -1)
		{
			cur = parent;
			parent = parent->_parent;
		}
		else if(parent->bf==2||parent->bf==-2)
		{
			if (parent->bf == 2 && cur->bf == 1)
			{
				RotateL(parent);
			}
			else if (parent->bf == -2 && cur->bf == 1)
			{
				RotateLR(parent);
			}
			else if (parent->bf == 2 && cur->bf == -1)
			{
				RotataRL(parent);
			}
			else if (parent->bf == -2 && cur->bf == -1)
			{
				RotateR(parent);
				
			}


		}
		else
		{
			assert(false);
		}
	}
	return true;
}

首先当根节点为空时直接插入并返回，如果不为空则按二叉搜索树的方法找到待插入的节点并进行赋值，其中赋值包括父节点指针的赋值以及平衡因子的赋值，左树加加右树减减，如果此时平衡因子为0，说明整棵树不会出现不平衡的情况，直接结束循环，如果此时平衡因子为1或-1，说明此子树不会出现不平衡的情况，但它的祖先节点可能会出现不平衡的状况，需要向上调整。如果此时平衡因子为2或-2，说明此时子树已经出现了不平衡的状况，需要进行旋转调整，旋转调整的口诀：父子同正左，父子同负右，父负子正左右，父正子负右左，按照不同的情况调用旋转函数

4.右单旋函数

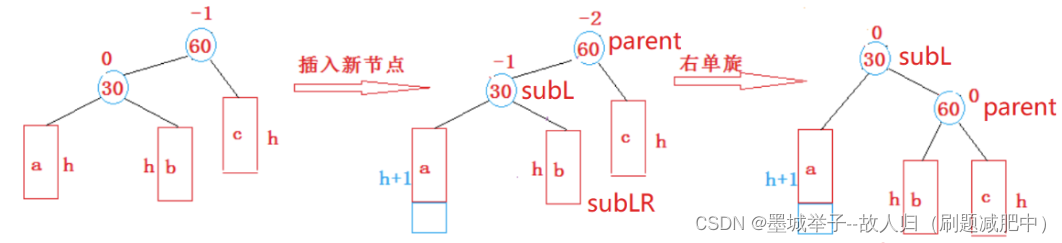
情景：原先abc树高度都为h，在a数插入一个节点后60节点开始不平衡，此时的解决方案是让60节点的父节点的指向60节点的指针指向30节点（有点绕），并将30节点未执行插入操作的子树到60节点的空子树处，并让60节点成为30节点的子树（另一棵子树是执行过插入操作的），以上操作也遵循了二叉搜索树的数据存放规则

	void RotateR(Node* parent)
	{
		Node* grandparent = parent->_parent;//找出祖先节点
		Node* childl = parent->left;//记录主要旋转子树
		if (grandparent)//存在祖先节点的情况 
		{
			if (grandparent->left == parent)
			{
				grandparent->left =childl;//把原先parent所占的位置用childl代替
			}
			else
			{
				grandparen->right = childl;
			}
		}
		else
		{
			root = childl;//没有祖先
		}
		childl->_parent = grandparent;//直接将主要旋转子树的父节点设置为祖先节点，如果没有祖先则为nullptr
		parent->left = childl->right;//把左子树的未被插入的树移接到之前的parent的左子树，注意二叉搜索树的取值范围
		childl->right->_parent = parent;//与上一条配合
		childl->right = parent;//正式右旋
		parent->_parent = childl;//与上一条配合
		childl->bf = parent->bf = 0;//调整完成，平衡因子归0
	}

5.左单旋函数

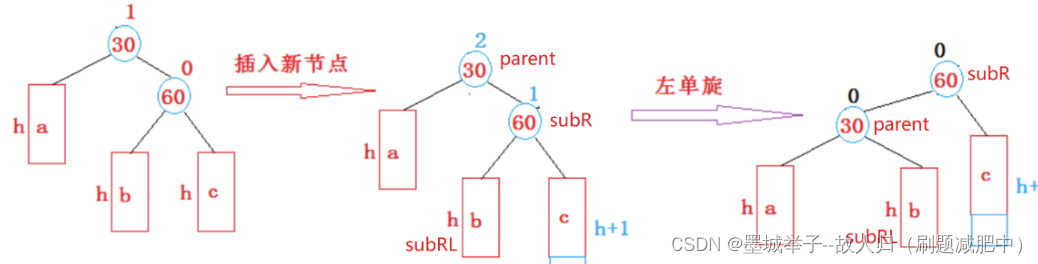
与左单旋类似，就是childr变成了childl,parent->left变成了parent->right

	void RotateL(Node*parent)
	{
		Node* grandparent = parent->_parent;//找出祖先节点
		Node* childr = parent->right;//记录主要旋转子树
		if (grandparent)//存在祖先节点的情况 
		{
			if (grandparent->left == parent)
			{
				grandparent->left = childr;//把原先parent所占的位置用childl代替
			}
			else
			{
				grandparen->right = childr;
			}
		}
		else
		{
			root = childr;//没有祖先
		}
		childr->_parent = grandparent;
		parent->right = childr->left;
		childr->left->_parent = parent;
		childr->left = parent;
		parent->_parent = childr;
		childr->bf = parent->bf = 0;
	}

6.右左旋函数和左右旋函数

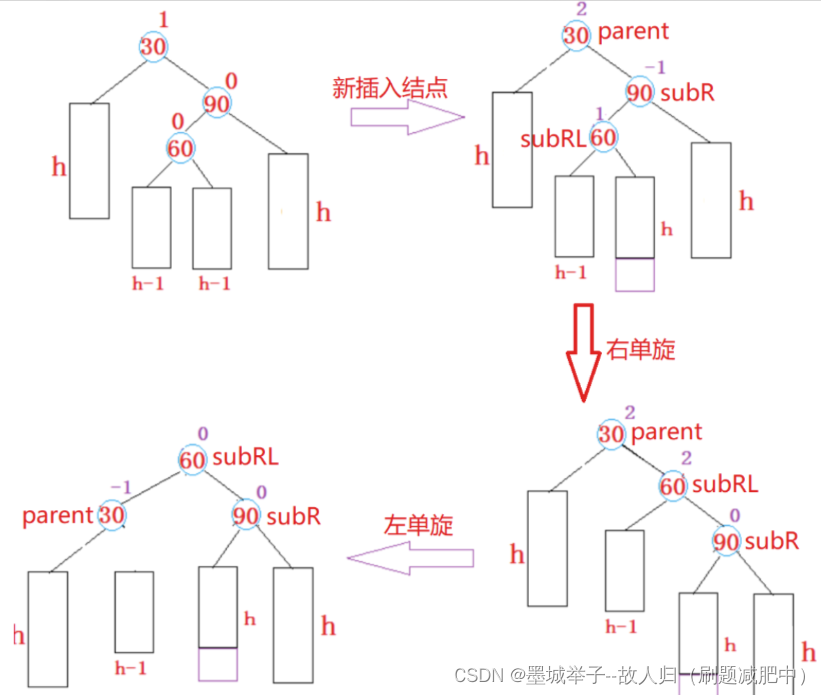
使用右左旋函数和左右旋函数的情景是父节点出问题的树与子节点新插入的树不在同一边，所以需要先对子树（子树为parent的与旋转方向相同方向的节点）进行旋转（旋转方向与新插入子树方向相反），再对父节点进行旋转（旋转方向与子树旋转方向相反）

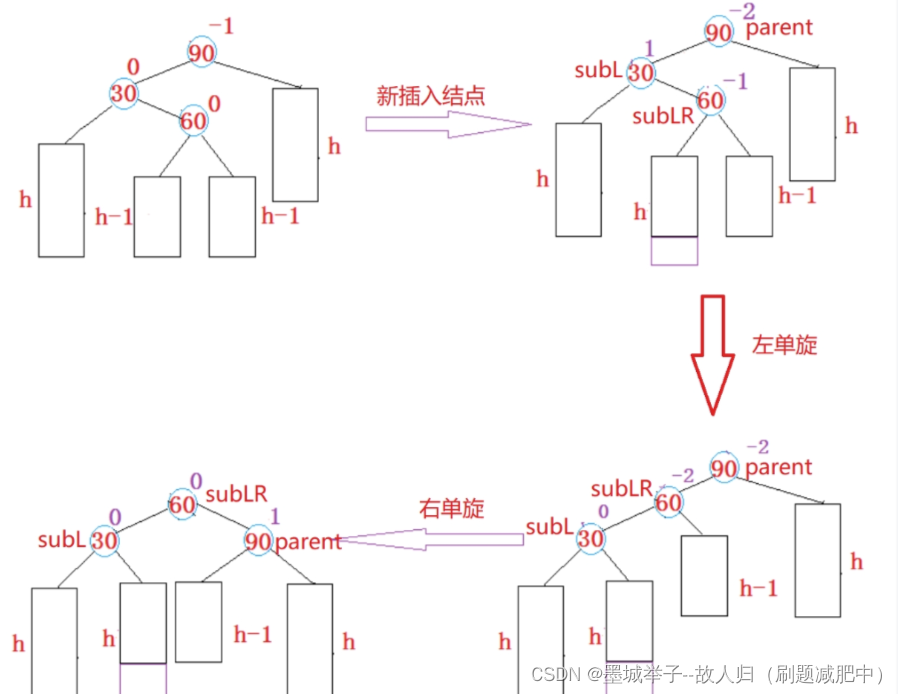
左右旋函数同理

接下来对二者进行节点调整，调整的对象是旋转后的子树的与旋转方向相反的子节点，调整的方面有三个，一个是parent的节点，一个是子节点，一个是子节点同方向的下一个节点我们称为新节点，调整规则是0则都0，1右左父左右子-1，-1右左新-1左右父1

void RotateRL(Node* parent)
{
	Node* childr = parent->right;
	int lbf = childr->left->bf;
	RotateR(childr);
	RotateL(parent);
	if (lbf == 0)
	{
		parent->bf = 0;
		childr->bf = 0;
		childr->left->bf = 0;
	}
	else if (lbf == 1)
	{
		parent->bf = -1;
		childr->bf = 0;
		childr->left->bf = 0;
	}
	else if (lbf == -1)
	{
		parent->bf = 0;
		childr->bf = 0;
		childr->left->bf = -1;
	}
	else
	{
		assert(0);
	}
}

	void RotateLR(Node* parent)
	{
		Node* childl = parent->left;
		int rbf = childl->right->bf;
		RotateR(childl);
		RotateL(parent);
		if (rbf == 0)
		{
			parent->bf = 0;
			childl->bf = 0;
			childl->right->bf = 0;
		}
		else if (rbf == 1)
		{
			parent->bf = 0;
			childl->bf = -1;
			childl->right->bf = 0;
		}
		else if (rbf == -1)
		{
			parent->bf = 1;
			childl->bf = 0;
			childl->right->bf = 0;
		}
		else
		{
			assert(0);
		}
	}

7.旋转总结

当根节点不平衡，平衡因子为2或-2时，分以下情况考虑

1.平衡因子为2，说明右子树高，那么再来看根节点的右节点的平衡因子，当此节点的平衡因子为1时，执行左单旋，为-1执行右左双旋

2.平衡因子为-2，说明左子树高，那么再来看根节点的左节点的平衡因子，当此节点的平衡因子为-1时，执行右单旋，为-1执行左右双旋时与平衡因子为2时的情况不同，它执行完成后根节点所在的树已经平衡不需要继续进行向上调整

8.验证平衡二叉树

1.验证avl树分为两个步骤，一个是验证二叉搜索树，其次是验证平衡性

验证二叉搜索树:验证中序遍历会得到一个有序的序列

	void Inorde(Node* root,vector<pair<K,V>>&v)
	{
		if (root == nullptr)
			return;
		Inorde(root->_left, v);
		v.push_back(root->_val);
		Inorde(root->_right, v);
	}

2.验证平衡性：高度差是否不相差超过1，且平衡因子没有计算错误

int high(Node* root)
{
	if (root == nullptr)
		return 0;
	int left = high(root->left);
	int right = high(root->right);
	int x = left > right ? left : right;
	return 1 + x;
}
bool _IsBalanceTree(Node* pRoot)
{
 // 空树也是AVL树
 if (nullptr == pRoot) return true;
    
 // 计算pRoot节点的平衡因子：即pRoot左右子树的高度差
 int leftHeight = _Height(pRoot->_pLeft);
 int rightHeight = _Height(pRoot->_pRight);
 int diff = rightHeight - leftHeight;
// 如果计算出的平衡因子与pRoot的平衡因子不相等，或者
 // pRoot平衡因子的绝对值超过1，则一定不是AVL树
 if (diff != pRoot->_bf || (diff > 1 || diff < -1))
 return false;
 // pRoot的左和右如果都是AVL树，则该树一定是AVL树
 return _IsBalanceTree(pRoot->_pLeft) && _IsBalanceTree(pRoot-
>_pRight);
 }

9.AVL树的性能分析

1.优势：它是一棵绝对平衡的二叉搜索树，保证了搜索的时间复杂度为O(longn)

2.劣势：修改困难，只有查找多修改少的应用场景适合AVL树