图/图的存储/图的遍历

图的概念：图的数据结构由两个集合构成，一个是顶点集V (vertex)，一个是边集E（Edge）；无向图一般记为G(V , E) ；有向图记为 G<V， E>

有向图就是边的指向是有方向区分的，例如从A->B ；从A可以到B，但是B不能到A（有向图的边是一个箭头，称之为弧，弧头是w，弧尾是v）
无向图的边是无方向区分的，只要A-B，从A可以到B，从B也可以到A

重要概念如下：

1:图一定不可以是空图，也就是说顶点集一定不能为空，边集可以为空
2:完全图：若任意两个顶点之间都存在着边（注意这里的边是任意两个顶点直接相连的边），则称该图是完全图。
无向完全图有n*(n-1) / 2 条边。
有向完全图有n*(n-1) 条边
3:子图：图中的某一部分顶点和一部分与顶点相连的边构成的新图，即是子图。（注意一定不能是简单的说“边的子集”和“顶点的子集”，必须是与顶点相连的边才可以构成子图）

针对无向图来说，超级重要的概念有：

4:连通：若从顶点A到顶点B有路径存在，则称AB是连通的
5:连通图和非连通图：如果图中任意两个顶点都有路径存在（不一定是直接相连的路径，这里注意跟完全图概念区分），则称该图为连通图，其实也就是字面意思“整张图是连通的”，如果有某些顶点与其它顶点并不连通，即某些顶点时孤立的，则称为非连通图。
6:连通分量（也称极大连通子图）：一张图G中假如有ABC连通，DE连通，则称之有两个连通分量，即两个极大连通子图（也就是图G中，连通的子图）。

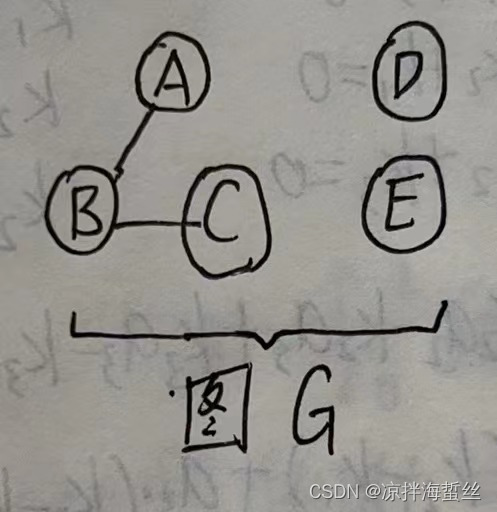
（7）对于无向图来说，N个顶点，至少需要N-1条边，才能形成连通图（画图好理解），如果N个顶点需要构成完全图，最少需要n*(n-1)/2条边。
如果边数小于n-1，则该图肯定是非连通图。

针对有向图来说，超级重要的概念有：

8:强连通：这个概念跟无向图的连通一定要区分，因为有向图是有向的，所以它的连通一定是“更强”的连通，所以记强连通。若AB强连通，则一定要有A->B 以及 A<- B；也就是两个方向都必须有，才能称为强连通。
9:强连通图：若有向图G中，图中任意两个顶点都有路径存在（不需要直接连接的路径，可以经过N个顶点，只要能有路径），则图G是强连通图
10:强连通分量（也称极大强连通子图）：跟无向图连通分量的概念一定要区分，强连通分量是指子图中一定要存在环，所以判断一个有向图是否存在强连通分量，一定要去找环，如果无环，证明最后一个顶点D无法回溯到第一个顶点A，也就是D到A没有路径，那么就不是强连通的。
11:对于有向图来说，N个顶点的有向图，最少最少需要n条边（构成一个环），才能构成强连通图。要构成有向完全图（有向完全图一定是强连通图，任意顶点都有来回两个箭头路径），则需要n*(n-1)条边。

极大连通子图和极小连通子图：

12:都是针对无向图的说法，极大和极小的区别，就在于极大必须包含该子图的所有的边，也就是说不单止要连通，还要保留全部边。极小连通子图只需要保留保证图连通的最少的边数，也就是说能连通就行。
注意⚠️：生成树是极小连通子图，生成树不是极大连通子图（因为不会包含所有边），所以生成树当然就不是连通分量

稠密图和稀疏图：

13:稠密和稀疏是针对边来说的，边数多就是稠密，边数少就是稀疏。（想像成渔网，边数多，整张网就很密，边数少，整张网就很稀疏）

图的例题：

（1）N个顶点N条边的无向图，一定是有环的（画图可以发现，若每个顶点都有一条边，则一定有环）；但是注意有环不一定连通，是否连通还要看边数（若n个结点的无向图有n*(n-1)/2条边，则一定一定是完全图，完全图一定是连通的且有环的）和从某个顶点进行深搜或者广搜是否可以遍历整张图。

（2）图的遍历并不是单纯的从某个顶点出发遍历其余顶点。因为图有可能是非连通的，单纯从某个顶点开始，只能遍历某张子图，其余子图中的顶点是遍历不到的，所以要遍历图，必须循环遍历顶点集V，遍历过的顶点打上标记，若一次遍历完成之后还有某些顶点未被打上遍历标记的ÿ