算法是用系统的方法解决实际问题的策略机制,算法的质量将影响到程序的效率,而时间复杂度则是评判时间复杂度的标准,时间复杂度越小,算法越好,程序执行效率越高,反之,效率越差。
【表示方法】
大O表示法:
当且仅当存在正常数c和n0,使得
T(n)<=cf(n)
对所有的n>n0成立。T(n)=O(f(n))称为算法的渐进时间复杂度,简称时间复杂度。(f(n)是问题规模n的某个函数)。例如:T(n)= n^2+4n+1,则可以用数学助记符号O(n^2)表示时间复杂度。
分析:(1)f(n)是n足够大时,对T(n)起支配作用的表达式。
(2)时间复杂度跟f(n)前面的系数关系不大。
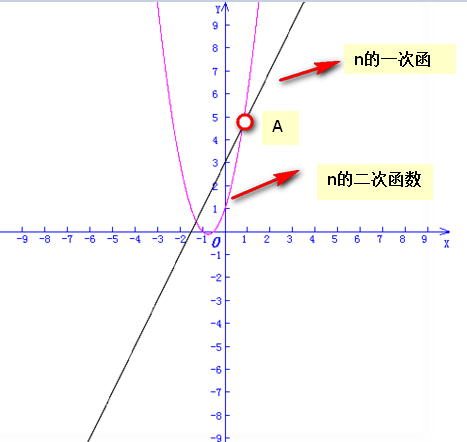
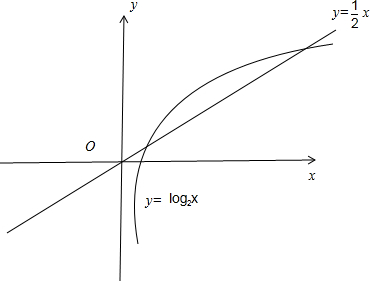
图1 n的二次方与一次方对比图 图2 一次方与log2X的对比图
由图1可明显看出,n^2与n做对比,始终会存在一个点A,前者超过后者,因此起决定作用的是n^2;由图2可以看出,x对比log2x,x起决定作用。
【常见算法复杂度】
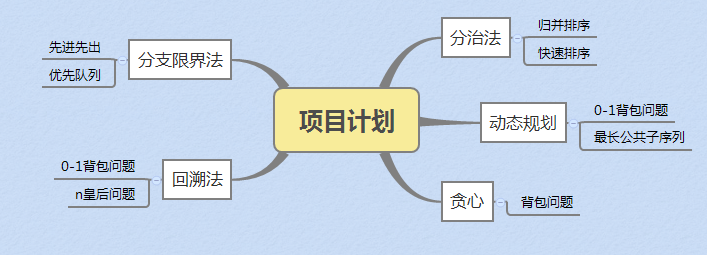
常见的算法设计分为5大类:
经典排序算法:
算法时间复杂度与算法的构成是紧密结合的,并不是准确的比较或者交换次数,而是一个概数,且在不同的条件下比较或者交换次数是不同的,可分为最坏时间复杂度,最好时间复杂度,平均时间复杂度,默认情况下算的是最坏复杂度。
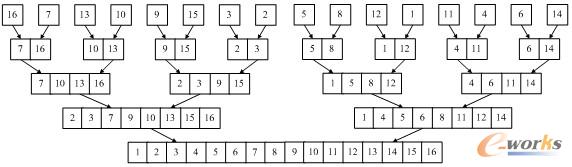
1. 归并排序复杂度
归并排序体现的是分组思想,现采用上面16个数的排序(体现特殊情况)对应一般情况的分析方法:
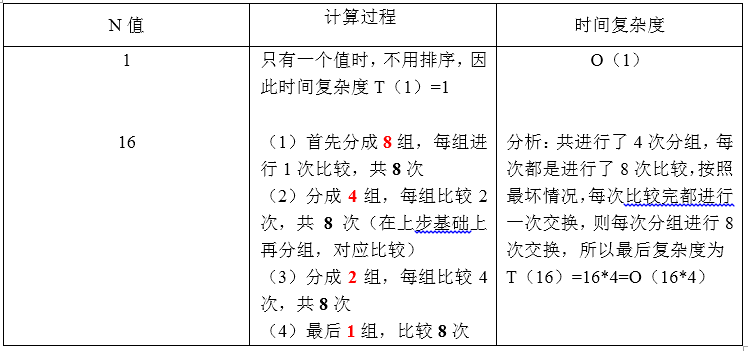
根据上面16个数排序的特殊情况来归纳一般情况(n):
(1)计算每次分组比较+交换次数:n
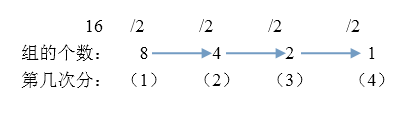
(2)共进行了几次分组:
由上图可以得出,组的个数都是在原来的基础上/2得到的,到1为止,因此,共进行几次分组,即n可以进行几次二分运算,为log2(n).
(3)总复杂度为:O(n*log2(n))
2. 0-1背包问题复杂度
0-1背包问题的实现时嵌套在两个循环里的,具体实现请看上篇博文《动态规划算法》。
3. 快速选择算法复杂度
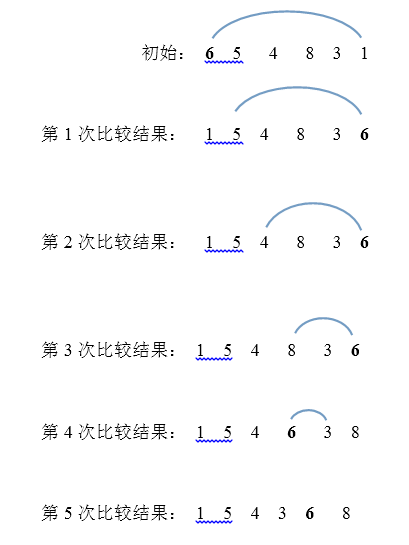



【总结】
研究文档下载地址:http://wenku.baidu.com/view/eb65c8f3a98271fe900ef90e






















 1045
1045

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








