平衡二叉树 之 AVL树

AVL树是最先发明的自平衡二叉查找树。AVL树以其发明者前苏联学者 G.M. Adelson-Velsky 和 E.M. Landis 名字而命名，他们在1962年的论文《An algorithm for the organization of information》中发表了它。[参考WiKI]

AVL树中，一个非常重要的概念为平衡因子（Balance factor），对于任意节点 x ，其平衡因子定义为该节点右子树和左子树高度差，即 bf（x）=h（x-right）-h（x-left）。

带有平衡因子1、0或 -1的节点被认为是平衡的。带有平衡因子 -2或2的节点被认为是不平衡的，并需要重新平衡这个树。平衡因子可以直接存储在每个节点中，或从可能存储在节点中的子树高度计算出来。

1. AVL树数据结构

为了方便计算每个节点的平衡因子，对二叉树的数据结构进行修改，增加一个数据单元用于记录以该节点为root的子树高度，重新定义数据结构如下：

struct BinaryTreeNode {
	keyType key;
	int height; //记录以该节点为root的树高度
	BinaryTreeNode* left; // left child
	BinaryTreeNode* right; // right child
};

// define AVL node
typedef BinaryTreeNode avlnode;

// define AVL tree
typedef BinaryTreeNode avltree;


// 比较左右子树高度，取最大的
int maxh(int ha, int hb) {
    return ha > hb ? ha : hb;
}

// 计算树的高度
int height(avltree* tree) {
    if (NULL == tree) return 0; 
    return tree->height;
}

2. AVL树旋转操作

AVL在插入和删除节点造成不平衡的时候需要对发生不平衡的节点及时调整，调整方法为旋转操作。根据造成不平衡的节点出构型可分为：LL 、RR 、LR 、RL型，对应的操作则为单旋和双旋，下面分析一下各种构型具体操作方法。

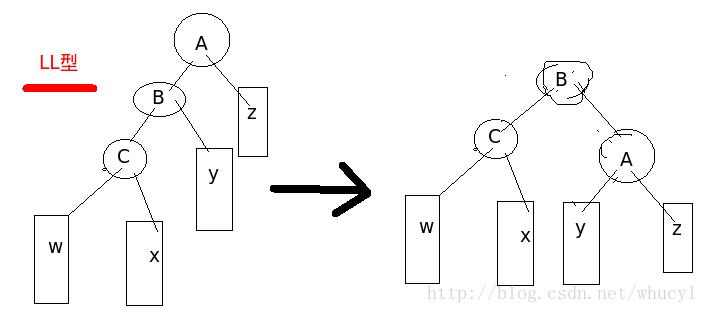
下图所示为LL构型，在B节点的左子树上插入节点导致A节点失衡，调整过程为：以B节点为轴心，A节点顺时针旋转至B的右子树，A的右子树又B的右子树代替。通过右旋操作，返回以B为Root的平衡子树。 RR够型和LL够型成对称关系，操作方向相反，此处就省略了。

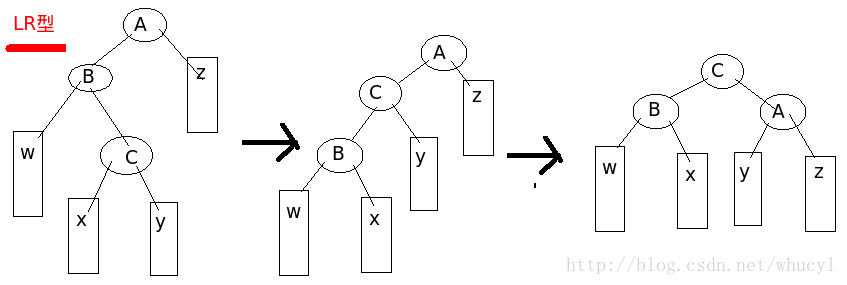
下图所示为LR构型，在B节点的右子树上插入新节点导致A节点失衡，调整过程分两个步骤：首先以C为轴心，B绕C逆时针旋转，生成的子树作为A的左子树；这样就变化成了LL型，然后用上图所示的方法调整即可。通过先左旋后右旋，返回以C为Root的平衡子树。RL型和LR型呈对称状，此处也省略。

下表列出节点够型和选择操作关系。

构型	操作	对应的函数
LL型	单旋： 右旋	// single right rotate for LL model avlnode* singleRightRotate(avlnode* aNode) {     avlnode* bNode = aNode->left;     // rebuild relation     aNode->left = bNode->right;     bNode->right = aNode;     // adjust the height     aNode->height = maxh(height(aNode->right), height(aNode->left)) + 1;     bNode->height = maxh(height(bNode->right), height(bNode->left)) + 1;     return bNode; }
RR型	单旋： 左旋	// single left rotate for RR model avlnode* singleLeftRotate(avlnode* aNode) {     avlnode* bNode = aNode->right;     // rebuild relation     aNode->right = bNode->left;     bNode->left = aNode;     // adjust height     aNode->height = maxh(height(aNode->right), height(aNode->left)) + 1;     bNode->height = maxh(height(bNode->right), height(bNode->left)) + 1;     return bNode; }
LR型	双旋： 先左旋 后右旋	// double rotate for LR model // left rotate first and then right rotate avlnode* leftRightRotate(avlnode* aNode) {     aNode->left = singleLeftRotate(aNode->left);     return singleRightRotate(aNode); }
RL型	双旋： 先右旋 后左旋	// double rotate for RL model // right rotate first and then left rotate avlnode* rightLeftRotate(avlnode* aNode) {     aNode->right = singleRightRotate(aNode->right);     return singleLeftRotate(aNode); }

3. 插入节点

向AVL树中插入节点后，要判断是否引起失衡，如果失衡则需要进一步确定构型，选择合适的基本旋转操作来调整。

// insert a key to AVL tree.
avlnode* avl_inssert(avltree* &tree, keyType key) {
    if (NULL == tree) {
        tree = (avlnode*) malloc(sizeof(avlnode));
        tree->key = key;
        tree->height = 1;
        tree->left = tree->right = NULL;
    } else if (key > tree->key) { // insert into the right subtree
        tree->right = avl_inssert(tree->right, key);
        int balanceFactor = height(tree->right) - height(tree->left);
        if (balanceFactor == 2) {
            if (key > tree->right->key) { // RR 型 , 右侧单旋
                tree = singleLeftRotate(tree);
            } else { // RL型 , 右侧双旋
                tree = rightLeftRotate(tree);
            }
        }
    } else if (key < tree->key) { // insert into the left subtree
        tree->left = avl_inssert(tree->left, key);
        int balanceFactor = height(tree->left) - height(tree->right);
        if (balanceFactor == 2) {
            if (key < tree->left->key) { // LL型 , 左侧单旋
                tree = singleRightRotate(tree);
            } else { // LR型 ， 左侧双旋
                tree = rightLeftRotate(tree);
            }
        }
    } else { // if the key is already exists, nothing to do....
    }
    // 重新计算树的高度
    tree->height = maxh(height(tree->left), height(tree->right)) + 1;

    return tree;
}

4. 删除节点

从AVL树中删除节点分为两个步骤：首先删除节点；然后调整平衡。删除操作对应为插入操作的逆向操作，调整平衡的时候也需要确定被删除节点的分支构型来选择合适的旋转方法。

// delete the given key from AVL tree.
avlnode* avl_delete(avltree* &tree, keyType key) {
	if (NULL == tree) {
		return NULL;
	}
	// delete the node with the given key
	if (key > tree->key) { // key exists in the right subtree
		tree->right = avl_delete(tree->right, key);
	} else if (key < tree->key) { // key exists in the left subtree
		tree->left = avl_delete(tree->left, key);
	} else {
		if (NULL != tree->left) { // when left is not NULL
			// find max node if left tree
			avlnode* dn = NULL;
			for (dn = tree->left; NULL != dn->right; dn = dn->right) {
			}
			// change the value
			tree->key = dn->key;
			// delete the max node
			tree->left = avl_delete(tree->left, dn->key);
		} else if (NULL != tree->right) { // when the right tree is not NULL
			// find the minimal node
			avlnode* dn = NULL;
			for (dn = tree->right; NULL != dn->left; dn = dn->left) {
			}
			// change the value
			tree->key = dn->key;
			// delete the minimal node
			tree->right = avl_delete(tree->right, dn->key);
		} else {			// when the node has no child
			free(tree);
			// the tree is Empty now, no need to do any operation
			return NULL;
		}
	}
	// adjust the tree to balance state after deletion
	if (height(tree->left) - height(tree->right) == 2) { // when the left subtree is too high
		if (height(tree->left->right) - height(tree->left->left) == 1) { // LR model
			tree = leftRightRotate(tree);
		} else { // LL model
			tree = singleRightRotate(tree);
		}
	} else if (height(tree->left) - height(tree->right) == -2) { // when the right subtree is too high
		if (height(tree->right->left) - height(tree->right->right) == 1) { // RL model
			tree = rightLeftRotate(tree);
		} else { // RR model
			tree = singleLeftRotate(tree);
		}
	} else {
		// the tree is already balanced, nothing to do ...
	}

	// recalculate the height of the tree.
	tree->height = maxh(height(tree->right), height(tree->left)) + 1;

	return tree;
}

5. 测试

分别对 查找二叉树 和  AVL树进行下列操作：依次插入 0-15 ；依次删除 0, 3，6，10，15 

测试结果如下：

测试查找二叉树 ： 依次插入 0 -15 构建如下： 前序 : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 中序 : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 依次删除 0, 3，6，10，15 之后： 前序 : 1 2 4 5 7 8 9 11 12 13 14 中序 : 1 2 4 5 7 8 9 11 12 13 14

测试 AVL 平衡二叉树 ： 依次插入 0 -15 构建如下： 前序 : 7 3 1 0 2 5 4 6 11 9 8 10 13 12 14 中序 : 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 依次删除 0, 3，6，10，15 之后： 前序 : 7 2 1 5 4 11 9 8 13 12 14 中序 : 1 2 4 5 7 8 9 11 12 13 14

对比来看， 查找二叉树退化为线性，而AVL树则形态匀称.