分治法的基本思想与例子解析

    分治法的设计思想：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

    凡治众如治寡，分数是也。——孙子兵法

1.基本思想

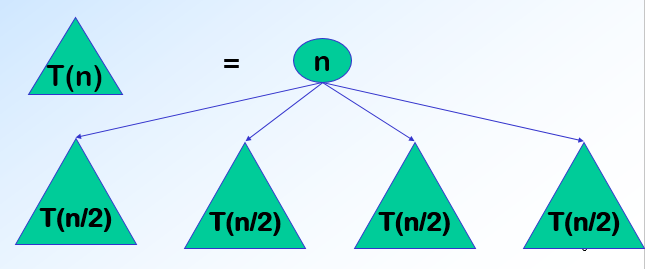
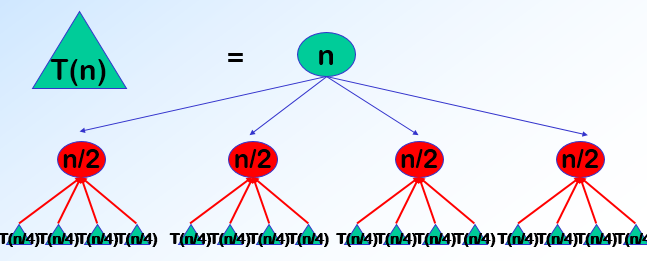
(1) 将求解的较大规模的问题分割成k个更小规模的子问题。

(2) 对这k个子问题分别求解。如果子问题的规模仍然不够小，则再划分为k个子问题，如此递归的进行下去，直到问题规模足够小，很容易求出其解为止。

(3) 将求出的小规模的问题的解合并为一个更大规模的问题的解，自底向上逐步求出原来问题的解。

 

 

2.适用条件

分治法所能解决的问题一般具有以下几个特征：

I. 该问题的规模缩小到一定的程度就可以容易地解决；

II. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质

III. 利用该问题分解出的子问题的解可以合并为该问题的解；

IV. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。 

注意：

       如果各子问题是不独立的，则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然也可用分治法，但一般用动态规划较好。

3. 分治法的应用例子

(a) 快速排序

I. 分解(divide)：以a[p]为基准元素将a[p:r]划分为3段a[p:q-1]，a[q]和a[q+1,r]，使得a[p:q-1]中任何元素小于等于a[q]，a[q+1,r]中任何元素大于等于a[q]。下标q在划分过程中确定。

II. 递归求解(conquer)：通过递归调用快速排序算法，分别对a[p:q-1]和a[q+1,r]进行排序。

III. 合并(merge)：由于对a[p:q-1]和a[q+1,r]的排序时就地进行的，所以在a[p:q-1]和a[q+1,r]都已排好的序后不需要执行任何计算，a[p:r]就已排好序。

package Sort;
/**
 * @author LIn
 * 算法名称：快速排序
 * 算法描述：
 * 1.通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小
 * 2.重复步骤1对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
 *
 * 复杂度分析：
 * 1.平均时间复杂度：O(nlogn)
 * 2.空间复杂度：O(logn)(最值元素存储空间)
 */
public class QuickSort {
	
	public static void quickSort(int[] a){
		quickSort(a, 0, a.length - 1);
	}

	private static void quickSort(int[] a, int left, int right){
		int pivotpos;  //划分后基准的位置
		if(left < right){
			pivotpos = Partition(a, left ,right);
			quickSort(a, left, pivotpos-1);
			quickSort(a, pivotpos+1, right);
		}
	}
	
	/**
	 * 普通选择基准
	 */
	private static int Partition(int[] a, int p, int r){
		//调用Partition(a,left,right)时，对a[left...right]做划分
		//并返回基准记录的位置
		int i = p, j = r + 1;
		int pivot = a[p];  //用区间的第一个记录作为基准
		
		while(true){
			while(a[++i] < pivot){}
			while(a[--j] > pivot){}
			if(i < j){
				swap(a, i, j);
			}
			else{
				break;
			}
		}
		
		swap(a, j, p);
		return j;
	}
	
	private static void swap(int[] a, int x, int y){
		int temp = a[x];
		a[x] = a[y];
		a[y] = temp;
	}

}

(b) 二分查找

       合并排序算法是用分治策略实现对n个元素进行排序的算法。其基本思想是：将待排序元素分成大小大致相同的2个子集合，分别对2个子集合进行排序，最终将排好序的子集合合并为所要求的排好序的集合。

package Sort;
/**
 * @author LIn
 * 算法名称：归并排序
 * 算法描述：
 * 1.将数组分为n等份(算法中为2)，对各子数组递归调用归并排序
 * 2.等分为2份时为2路归并，最后子数组排序结束后，将元素合并起来，复制回原数组
 * 
 * 复杂度分析：
 * 1.平均时间复杂度：O(nlogn)
 * 2.空间复杂度：O(n)(临时数据储存空间)
 */
public class MergeSort {
	
	/*public型的mergeSort是private型递归方法mergeSort的驱动程序*/
	public static void mergeSort(int[] a){
		int[] tempArray = new int[a.length];   //若数组元素为对象类型，需创建Comparable类的数组，再强转为该对象类型
		
		mergeSort(a, tempArray, 0, a.length - 1);
	}
	
	/**
	 * 递归调用归并排序
	 */
	private static void mergeSort(int[] a, int[] tempArray, int left, int right){
		if(left < right){
			int center = (left + right) / 2;
			mergeSort(a, tempArray, left, center);
			mergeSort(a, tempArray, center + 1, right);
			merge(a, tempArray, left, center + 1, right);   //子数组排序结束后，将子数组合并
		}
	}
	
	/**
	 * 合并左右的半分子数组
	 * @param a          需排序数组
	 * @param tempArray  临时存储数组
	 * @param leftPos    左半子数组开始的下标
	 * @param rightPos   右半子数组开始的下标
	 * @param rightEnd   右半子数组结束的下标
	 */
	private static void merge(int[] a, int[] tempArray, int leftPos, int rightPos, int rightEnd) {
		int leftEnd = rightPos - 1;
		int tempPos = leftPos;
		int num = rightEnd - leftPos + 1;
		
		//主循环
		while(leftPos <= leftEnd && rightPos <= rightEnd){
			if(a[leftPos] <= a[rightPos]){
				tempArray[tempPos++] = a[leftPos++];
			}else{
				tempArray[tempPos++] = a[rightPos++];
			}
		}
		/*比较结束后，只会有一个子数组元素未完全被合并*/
		while(leftPos <= leftEnd){        //复制左半子数组剩余的元素
			tempArray[tempPos++]  = a[leftPos++];
		}
		while(rightPos <= rightEnd){      //复制右半子数组剩余的元素
			tempArray[tempPos++]  = a[rightPos++];
		}
		
		//将元素从临时数组赋值回原数组
		for(int i = 0; i < num; i++, rightEnd--){
			a[rightEnd] = tempArray[rightEnd];
		}
		
	}

}

参考资料：

1. 《算法设计与分析》

2. 《算法》