Kruskal---求最小生成树（贪心算法）

最新推荐文章于 2023-05-30 08:55:36 发布

爱橙子的OK绷

最新推荐文章于 2023-05-30 08:55:36 发布

阅读量3.4k

点赞数

CC 4.0 BY-SA版权

分类专栏：算法系列文章标签：最小生成树 kruskal

本文链接：https://blog.csdn.net/will130/article/details/46335447

Kruskal算法是一种贪心策略，用于找到加权无向图的最小生成树。它按边的权重递增顺序选择边，但避免形成环。算法包括将边排序、使用并查集维护边的连通性状态，直至添加(V - 1)条边形成最小生成树。时间复杂度为O(ElogE)或O(ElogV)，适用于稠密图。

算法描述：

一个图的生成树是一个树并把图的所有顶点连接在一起。一个图可以有许多不同的生成树。最小生成树其实是最小权重生成树的简称。

最小生成树有（V – 1）条边，其中V是给定的图的顶点数量。

Kruskal算法是一种贪心算法。贪心的选择是选择最小的权重的边，并不会和当前的生成树形成环。

算法步骤：

1,按照所有边的权重排序(从小到大)

2,选择最小的边。检查它是否形成与当前生成树形成环。如果没有形成环，将这条边
加入生成树。否则，丢弃它。  

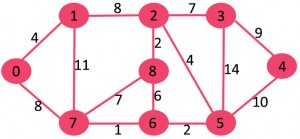
3,重复第2步，直到有生成树（V-1）条边

求下图的最小生成树（MST:minimum spanning tree）

这里写图片描述

该图有9个节点，14条边，MST有8条边。
将每条边按权重排序如下（从小到大）：

Weight   Src    Dest
1         7      6
2         8      2
2         6      5
4         0      1
4         2      5
6         8      6
7         2      3
7         7      8
8         0      7
8         1      2
9         3      4
10        5      4
11        1      7
14        3      5

依次选择边：

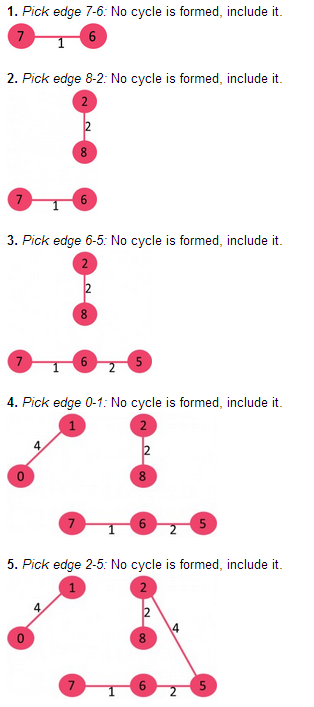
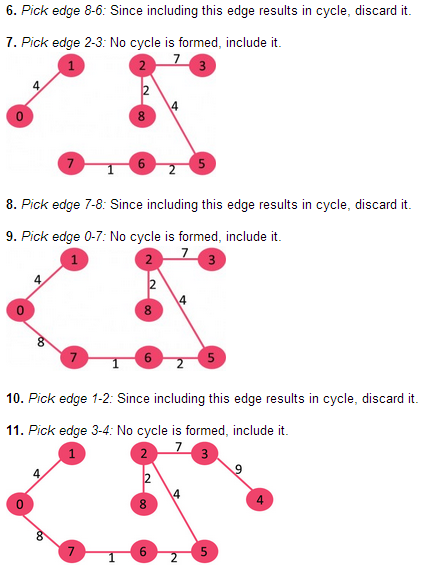
这里写图片描述

已经选择V-1条边，算法结束。

时间复杂度：

O(ElogE) 或 O(ElogV)。排序使用 O(ELogE) 的时间，之后我们遍历中使用并查集O(LogV) ，所以总共复杂度是 O(ELogE + ELogV)。E的值最多为V^2，所以
O(LogV) 和 O(LogE) 可以看做是一样的。

算法实现：

//Kruskal算法求无向带权图的最小生成树
#include <iostream>
#include<stdlib.h>
using namespace std;
//带权边的结构体
struct Edge
{
    int start;
    int end;
    int weight;
};
//无向图
struct Graph
{
    // V-> 顶点个数 E-> 边的个数
    int V,E;
    //图由边组成的数组来表示

最低0.47元/天解锁文章