Dijkstra---求单源最短路径（贪心算法）

算法步骤：

1) Create a set sptSet (shortest path tree set) that keeps track of vertices
included in shortest path tree, i.e., whose minimum distance from source is
calculated and finalized. Initially, this set is empty.
创建一个集合sptSet，用来保存包含在最短路径树中顶点的轨迹，其到源点距离已计算出来。集合初始为空。
2) Assign a distance value to all vertices in the input graph. Initialize all
distance values as INFINITE. Assign distance value as 0 for the source vertex so
that it is picked first.
对给定图中所有顶点都赋予一个距离值，初始化为无穷。源点距离值赋为0，从而可以最先选取。
3) While sptSet doesn’t include all vertices
当 sptSet还未包含所有顶点
….a) Pick a vertex u which is not there in sptSet and has minimum distance
value.
选取一个不在 sptSet中并且具有最小距离值的顶点u
….b) Include u to sptSet.
将u包含在 sptSet中
….c) Update distance value of all adjacent vertices of u. To update the distance
values, iterate through all adjacent vertices. For every adjacent vertex v, if sum
of distance value of u (from source) and weight of edge u-v, is less than the
distance value of v, then update the distance value of v.
更新所有跟u相邻定点的距离值。迭代遍历所有相邻顶点，以更新距离值。对于每一个相邻顶点v，if(dist[u]+weight < dist[v])，则更新dist[v]。

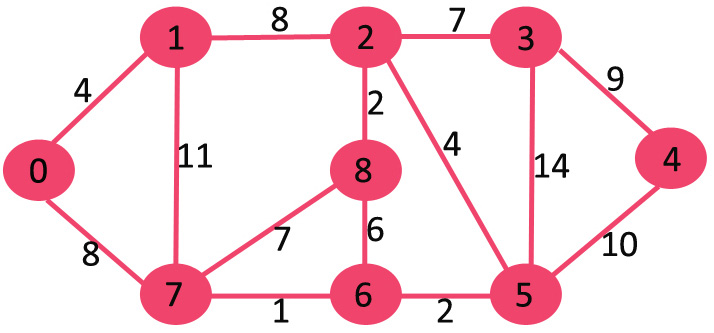
算法实例：

集合sptSet初始化为空，每个顶点的距离设定为{0, INF, INF, INF, INF, INF, INF, INF}。
选取有最小距离值的顶点，因此顶点0被选择，将其包含进sptSet集合。与0相邻的顶点为1和7，因此1和7的距离值分别被更新为4和8。

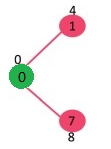
选择具有最小距离值并且不在 sptSET集合中的顶点。顶点1加入到 sptSET中。则 sptSET更新为{0,1}。更新与1相邻的顶点的距离值，顶点2的距离值变为12。

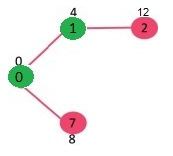
选择具有最小距离值并且不在 sptSET集合中的顶点。顶点7加入到 sptSET中。则 sptSET更新为{0，1，7}。更新与7相邻的顶点的距离值，顶点6和8的距离值分别更新为15和9。

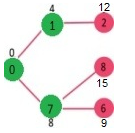
选择具有最小距离值并且不在 sptSET集合中的顶点。顶点6加入到 sptSET中。则 sptSET更新为{0，1，7，6}。更新与6相邻的顶点的距离值，顶点5和8的距离值分别更新为11和15。

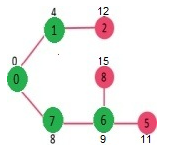
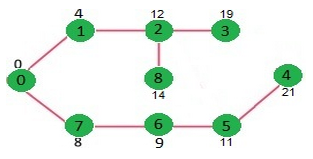
重复上述过程直到sptSET包含所有顶点。最终，我们得到如下最短路径树Shortest Path Tree (SPT)

算法实现：

bool型数组 sptSet[] 表示顶点是否包含在 SPT中。
数组dist[]用来存放每个顶点到源点的最短距离值。

#include <iostream>
#include <limits.h>

using namespace std;
//图中顶点数
const int V=9;
//从未包含在SPT的集合T中,选取一个到S集合距离最短的顶点。
int getMinIndex(int dist[V], bool sptSet[V])
{
    int min=INT_MAX,min_index;
    for(int v=0;v<V;v++)
    {
        if(sptSet[v]==false && dist[v]<min)
        {//!!!!!!!!!!!
            min=dist[v],min_index=v;
        }
    }
    return min_index;
}
//Dijkstra算法。图用邻接矩阵表示
void dijkstra(int graph[V][V], int source)
{
    //输出数组.dist[i]保存从源点到i的最短距离
    int dist[V];
    //sptSet[i]=true 如果顶点i包含在SPT中
    bool sptSet[V];
    // 初始化. 根据输入的邻接矩阵0代表不可达
    for(int i=0;i<V;i++)
    {
        dist[i]=(graph[source][i]==0?INT_MAX:graph[source][i]);
        sptSet[i]=false;
    }
    // 源点，距离总是为0. 并加入SPT
    dist[source]=0;
    sptSet[source]=true;

    // Find shortest path for all vertices
    for(int count=0;count<V-1;count++)
    {// 迭代V-1次，由于不用计算源点了，还剩下V-1个需要计算的顶点

        // u是T集合中到S集合距离最小的点
        int u=getMinIndex(dist, sptSet);
        // 加入SPT中
        sptSet[u]=true;

        //更新与u相邻的v的距离.可理解为Bellman-Ford中的松弛操作
        for(int v=0;v<V;v++)
        {
            /*更新dist[v]前提：v不在集合sptSet中
                            && v和u相邻(graph[u][v]非0)
                            && dist[u]!=INT_MAX&&dist[u]+graph[u][v]<dist[v]*/
            if(!sptSet[v]&&graph[u][v]&&dist[u]!=INT_MAX&&dist[u]+graph[u][v]<dist[v])
            {
                dist[v]=dist[u]+graph[u][v];
            }
        }
    }
    cout<<"Vertex   Distance from Source"<<endl;
    for(int i=0;i<V;i++)
    {
        cout<<i<<"\t\t"<<dist[i]<<endl;
    }
}
int main()
{
    /* 以例子中的图为例 */
    int graph[V][V] =
    { { 0, 4, 0, 0, 0, 0, 0, 8, 0 },
      { 4, 0, 8, 0, 0, 0, 0, 11, 0 },
      { 0, 8, 0, 7, 0, 4, 0, 0, 2 },
      { 0, 0, 7, 0, 9, 14, 0, 0, 0 },
      { 0, 0, 0, 9, 0, 10, 0, 0, 0 },
      { 0, 0, 4, 0, 10, 0, 2, 0, 0 },
      { 0, 0, 0, 14, 0, 2, 0, 1, 6 },
      { 8, 11, 0, 0, 0, 0, 1, 0, 7 },
      { 0, 0, 2, 0, 0, 0, 6, 7, 0 } };
    dijkstra(graph, 0);
    return 0;
}

执行结果：

Vertex   Distance from Source
0               0
1               4
2               12
3               19
4               21
5               11
6               9
7               8
8               14

参考：http://www.geeksforgeeks.org/greedy-algorithms-set-6-dijkstras-shortest-path-algorithm/