图机器学习基础知识——CS224W（12-motifs）

CS224W: Machine Learning with Graphs

Stanford / Winter 2021

12-motifs

Subgraphs and Motifs

Subgraphs and Motifs

Definition: Subgraph

Definition: Subgraph

• Node-induced subgraph

  • Take subset of the nodes and all edges induced by the nodes (由节点集和与这些节点相关的边所建立的子图)

  • $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$ is a node induced subgraph iff

    • $V^{\prime }\subseteq V$

    • E ′ = { ( u , v ) ∈ E ∣ u , v ∈ V ′ } E^{\prime}=\left\{(u, v) \in E \mid u, v \in V^{\prime}\right\} E′={(u,v)∈E∣u,v∈V′}

    • $G^{\prime }$ is the subgraph of $G$ induced by $V^{\prime }$

• Edge-induced subgraph

  • Take subset of the edges and all corresponding nodes (由边集和这些边对应的节点所建立的子图)

    • $G^{\prime }=\left(V^{\prime },E^{\prime }\right)$ is an edge induced subgraph iff

      • $E^{\prime }\subseteq E$

      • V ′ = { v ∈ V ∣ ( v , u ) ∈ E ′ V^{\prime}=\left\{v \in V \mid(v, u) \in E^{\prime}\right. V′={v∈V∣(v,u)∈E′ for some $u\}$

• The best definition depends on the domain (哪种定义适用取决于具体的问题)

  • Chemistry: node-induced (functional groups)

  • Knowledge graphs: Often edge-induced (focus is on edges representing logical relations)

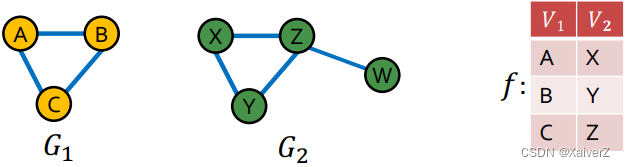
• Graph Isomorphism: Check whether two graphs are identical

  • $G_1=\left(V_1,E_1\right)$ and $G_2=\left(V_2,E_2\right)$ are isomorphic if there exists bijection $f:V_1\to V_2$ such that $(u,v)\in E_1$ iff $(f(a),f(b))\in E_2$ (若两张图存在一个双射函数，使一个图的所有节点能唯一映射到另一个图的节点，那么这两张图是同构的)

  

• 前述的定义中，无论是哪种方式，子图的节点和边都来自原图$G$。如果子图的节点和边来自于一个完全不同的图呢？

  • $G_2$ is subgraph-isomorphic to $G_1$ if some subgraph of $G_2$ is isomorphic to $G_1$

    • 也可以直接说$G_1$是$G_2$的一个子图

    • We can use either the node-induced or edge-induced definition of subgraph

  

• Case Example of Subgraphs

  

  

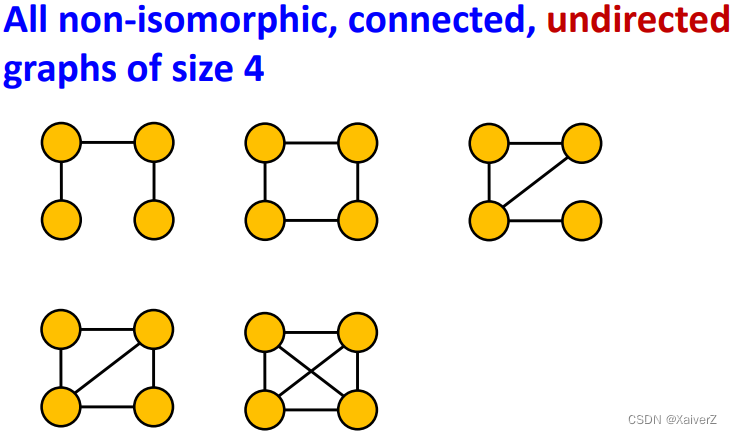
Network Motifs

Network Motifs

• Network Motifs: recurring, significant patterns of interconnections

  • Pattern: Small (node-induced) subgraph

  • Recurring: Found many times, i.e., with high frequency (How to define frequency?)

  • Significant: More frequent than expected, i.e., in randomly generated graphs (How to define random graphs?)

Subgraph Frequency

Subgraph Frequency

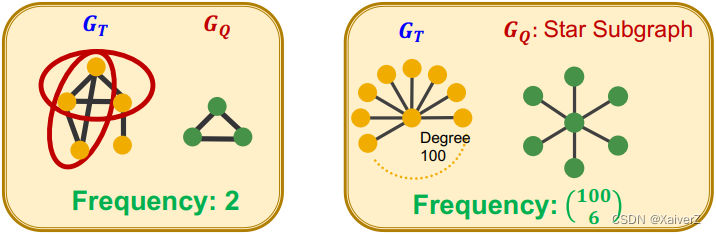
• Graph-level Subgraph Frequency Definition

  Let $G_Q$ be a small graph and $G_T$ be a target graph dataset

  • Frequency of $G_Q$ in $G_T$: number of unique subsets of nodes $V_T$ of $G_T$ for which the subgraph of $G_T$ induced by the nodes $V_T$ is isomorphic to $G_Q$

  

• Node-level Subgraph Frequency Definition

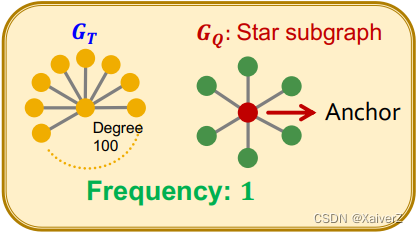
  Let $G_Q$ be a small graph, $v$ be a node in $G_Q$ (the “anchor”) and $G_T$ be a target graph dataset

  • The number of nodes $u$ in $G_T$ for which some subgraph of $G_T$ is isomorphic to $G_Q$ and the isomorphism maps $u$ to $v$ (不同子图的锚点不能重复)

  • Let $(G_Q,v)$ be called a node-anchored subgraph

  

Motif Significance

Motif Significance

• To define significance we need to have a null-model (i.e., point of comparison)

• Key Idea: Subgraphs that occur in a real network much more often than in a random network have functional significance (若一个子图在真实网络中出现的频率比在多个随机生成的统计相似的图中出现的平均频率还要高，那么就说明这个子图具备一定的显著性)

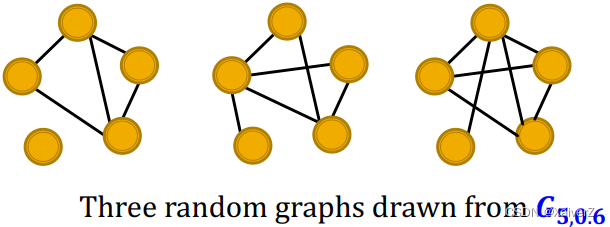
• Erdős–Rényi (ER) random graphs

  • $G_{n,p}$: undirected graph on $n$ nodes where each edge $(u,v)$ appears i.i.d. with probability $p$ (每两节点之间连边的概率为$p$)

  

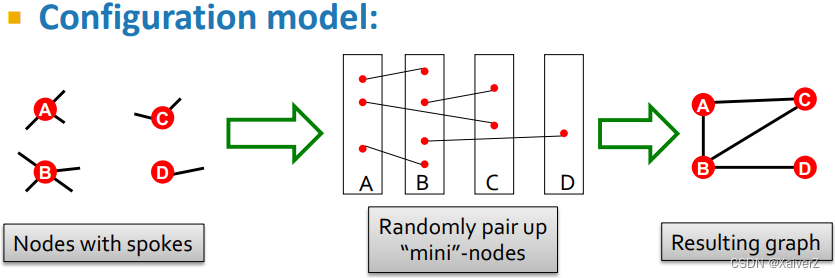
• Configuration Model

  • Generate a random graph with a given degree sequence $k_1,k_2,\dots k_N$ (节点的度分布要保持一致)

  • Useful as a “null” model of networks

    Null Model: Each $G^{rand}$ has the same #(nodes), #(edges) and degree distribution as $G^{real}$

    • We can compare the real network $G^{real}$ and a random $G^{rand}$ which has the same degree sequence as $G^{real}$

  

• Intuition: Motifs are overrepresented in a network when compared to random graphs

  • Step 1: Count motifs in the given graph ($G^{real}$) (在原图中统计motifs)

  • Step 2: Generate random graphs with similar statistics (e.g. number of nodes, edges, degree sequence), and count motifs in the random graphs (以与原图相似的统计信息构建多个随机生成图并分别统计motifs)

  • Step 3: Use statistical measures to evaluate how significant is each motif (使用一些统计评价标准衡量motifs significance)

    • Use Z-score

• Z-score for Statistical Significance

  • $Z_i$ captures statistical significance of motif $i$

    $$Z_i=\left(N_i^{\text{real }}-{\bar{N}}_i^{\text{rand }}\right)/\mathrm{std}\left(N_i^{\text{rand }}\right)$$
    其中，$N_i^{\text{real }}$为原图$G^{real}$中第$i$个motif的数量；${\bar{N}}_i^{\text{rand }}$为多个随机生成图中的第$i$个motif的平均频数；std为多个随机生成图中的第$i$个motif的标准差

  • Negative values indicate under-representation

  • Positive values indicate over-representation

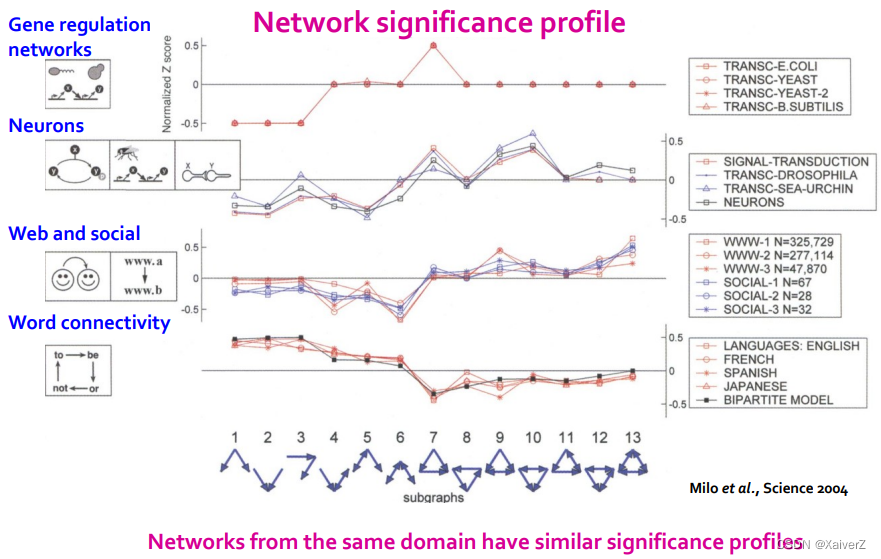
• Network significance profile (SP)

  $$S{P}_i=Z_i/\sqrt{\sum _j{Z}_j^2}$$

  • SP is a vector of normalized Z-scores

  • The dimension depends on number of motifs considered (维度取决于考虑多少个不同的motifs)

  • SP emphasizes relative significance of subgraphs (SP强调的是子图间的相对显著性程度)

• Example

  

Neural Subgraph Matching

Neural Subgraph Matching

• Task

  

  • 由于寻找子图是NP-hard，故使用神经网络来进行子图匹配

  

• Neural Architecture for Subgraphs

  • 这里要使用node-anchored neighborhoods，使用GNN捕捉$u$和$v$ (分别是Query和Target的锚点) 的representation，预测节点$u$的邻居结构是否与节点$v$的邻居结构同构

  • Why Anchor?

    • We not only predict if there exists a mapping, but also a identify corresponding nodes ($u$ and $v$)

  

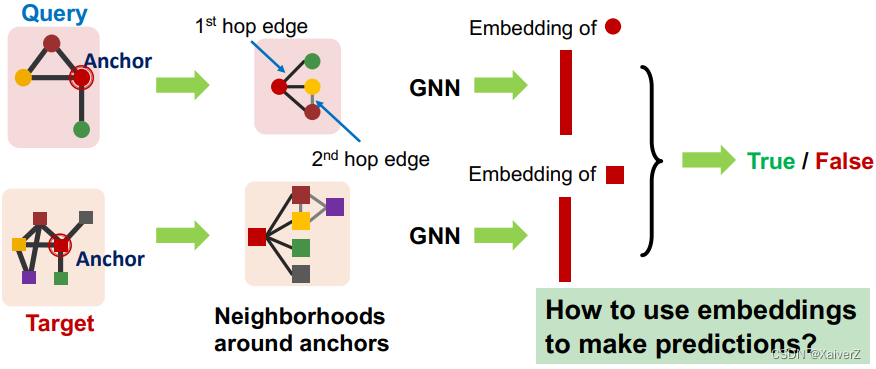
• Decomposing $G_T$ into Neighborhoods

  • For each node in $G_T$

    • Obtain a k-hop neighborhood around the anchor

    • Can be performed using breadth-first search (BFS)

    • The depth $k$ is a hyper-parameter (e.g. 3)

      • Larger depth results in more expensive model

  • Same procedure applies to $G_Q$ to obtain the neighborhoods

  • We embed the neighborhoods using a GNN (上述的步骤都可以用GNN来替代)

    • By computing the embeddings for the anchor nodes in their respective neighborhoods (在锚点各自的邻居结构中计算embeddings，与GNN的Message Passing过程完全对应)

Order Embedding Space

Order Embedding Space

• Capture Partial Ordering (偏序)

  左下的embedding是右上的embedding的子图

  

  

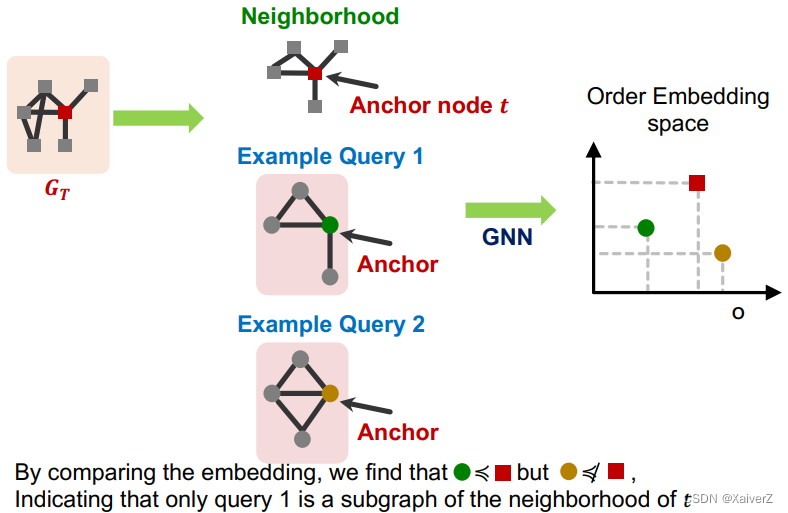
• Why Order Embedding Space?

  Subgraph isomorphism relationship can be nicely encoded in order embedding space (下述属性都完美对应到了Order Embedding Space中)

  • Transitivity (传递性): $G_1$是$G_2$的子图，$G_2$是$G_3$的子图，那么$G_1$是$G_3$的子图

  • Anti-symmetry (反对称性): $G_1$是$G_2$的子图，$G_2$是$G_1$的子图，那么$G_1$与$G_2$同构

  • Closure under intersection: 仅含一个节点的图是所有图的子图

  

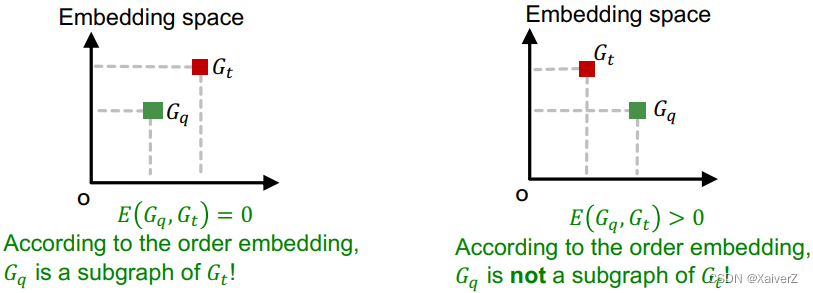
• Loss Function: Order Constraint

  • max-margin loss

    $$E\left(G_q,G_t\right)=\sum _{i=1}^D{\left(\max \left(0,z_q[i]-z_t[i]\right)\right)}^2$$

  

• Training Neural Subgraph Matching

  • To learn such embeddings, construct training examples $(G_q,G_t)$ where half the time, $G_q$ is a subgraph of $G_t$, and the other half, it is not

  • Train on these examples by minimizing the following max-margin loss

    • For positive examples: Minimize $$E(G_q,G_t)$$ when $G_q$ is a subgraph of $G_t$

    • For negative examples: Minimize $$\max \left(0,\alpha -E\left(G_q,G_t\right)\right)$$

      • Max-margin loss prevents the model from learning the degenerate strategy of moving embeddings further and further apart forever

• Training Example Construction

  

• Training Details

  

• Subgraph Predictions on New Graphs

  

Mining Frequent Motifs

Mining Frequent Motifs

• Finding Frequent Subgraphs (找出给定size-k下，在目标图中出现频率最大的子图，这里的子图匹配使用node-anchored subgraph)

  • Enumerating all size-k connected subgraphs

  • Counting #(occurrences of each subgraph type)

• Why is it Hard?

  • 给定size-k下的可能子图组合形式就已经需要很大计算量了

  • 判断子图从属关系是NP-hard，所以计数计算量也很大

SPMiner

SPMiner

• Overview: a neural model to identify frequent motifs

  

• Key Idea: order embedding之后，可以很方便的计算出以某个节点为锚点，k-hop (size-k)的子图在目标图中出现的频数，只需要计算该节点在embedding space中，有多少节点的embedding在vector space中位于它的右上区域

  

• SPMiner Search Procedure

  SPMiner采用一种搜索策略，从size-1的子图开始搜索，直到达到要求的size-k，并保证搜索到达size-k时，能找到size-k各子图频数的最大值

  • Initial step: 在目标图中随机选取一个节点$u$，令$S=u$

    

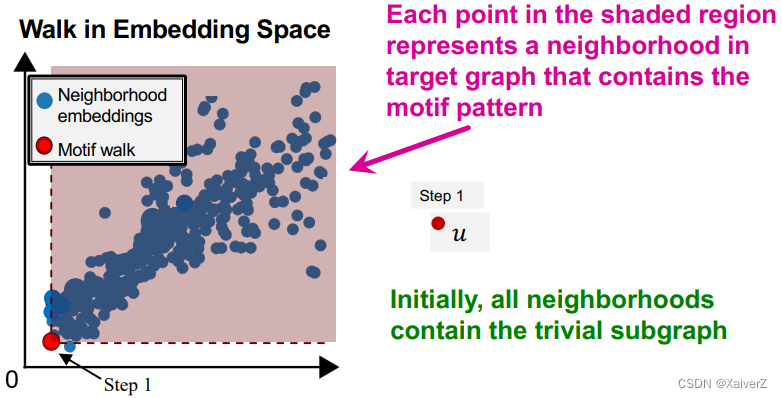
  • Iteratively: 通过不断迭代每次选取一个集合$S$中节点的邻居，并加入到$S$中，以此逐渐扩大motif的规模

    

    • 我们希望迭代时能不断找到频数最大的motifs

    • Total violation of a subgraph $G$: the number of neighborhoods that do not contain $G$

      • The number of neighborhoods $G_{N_i}$ that do not satisfy $Z_Q⩽Z_{N_i}$

      • Minimizing total violation = maximizing frequency

    • 基于上述定义，我们可以直接使用启发式贪心策略：在每一步迭代中，添加能使total violation最小的邻居节点

  • Termination: 直到达到指定的motif size-k，红色阴影区域的点数量即为size-k motif的最大频数