c实现一个简单的线性反馈移位寄存器LFSR

线性反馈移位寄存器

移位寄存器是流密码产生密钥流的一个主要组成部分。GF(2)上一个n级反馈移位寄存器由n个二元存储器与一个反馈函数组成，如图1。 若是a1, a2, ..., an 的线性函数，则称之为线性反馈移位寄存器（Linear Feedback Shift Register, LFSR），则 f 可写为

反馈函数是n元布尔函数，即n个变元 a1, a2, a3, ..., an 可以独立的取0和1这两个可能的值函数中的运算有逻辑与、或、补等运算，最后的值也为 0 或 1.

图1

 

举例：图2是一个3级反馈移位寄存器，其初始状态为 (a1,a2,a3) = (1, 0, 1)

注：该反馈函数为非线性：f(a1,a2,a3) = a1a2+a3,  是模2加法

图2

 

则该三级反馈移位寄存器的状态和输出如图3

图3

 

即输出序列为101110111011...，周期为4

c实现一个线性反馈移位寄存器代码

#include<stdio.h>

#define N 40
#define s_N 4

// 计算下一项
int a_n(int a[s_N], int b[s_N])
{
	int s = 0;
	for(int i=0;i<s_N;i++)
	{
		s = s+a[i]*b[i];
	}
	return s%2;
}

// 打印数组
void print(int a[], int len)
{	
	for(int i=0;i<len;i++)
	{
		printf("%d", a[i]);
	}	
	printf("\n");
}

// 判断两数组是否相等
bool judge(int a[s_N], int b[s_N])
{
	bool flag = 1;
	for(int i=0;i<s_N;i++)
	{
		if(a[i]!=b[i])
			flag = 0;
	}
	return flag;
}

// 找最小正周期
int T(int array[N])
{
	int t, j;
	int temp[s_N];  // 临时数组
	int goal_array[s_N];  // 匹配（目标）数组，为找到相同的以确定周期T
	bool flag = 0;

	for(int i=0;i<N-s_N;i++)
	{
	// 从第i个位置开始以四个单位为一个数组遍历
		for(int k=0;k<s_N;k++)
		{
			goal_array[k] = array[i+k];
		}
		if(flag)
			break;

		for(j=i+1;j<N-s_N-1;j++)
		// 从第i+1个位置开始以四个单位为一个数组遍历
		{
			for(int l=0;l<s_N;l++)
			{
				temp[l] = array[j+l];
			}
			flag = judge(temp, goal_array);
			if(flag)
			{
				break;
			}
		}
	}
	return t=j;
}

int main()
{
	int t;
	int a[N];
	int s[s_N] = {1, 1, 0, 1};
	int temp[s_N];
	int a_poly[s_N] = {0, 1, 1, 0};

/*	printf("a[n]: %d\n", a_n(s, a_poly));  // 计算下一项并输出 */
	
	// 输出前s_N项（一定会输出的）
	for(int i=0;i<s_N;i++)
	{
		a[i] = s[i];
	}

	for(int n=s_N;n<N;n++)
	{
		for(int j=0;j<s_N;j++)
		{
			temp[j] = a[n-s_N+j];
		}
		a[n] = a_n(temp, a_poly);
	}

	t = T(a);

	printf("输入的s: ");
    print(s, s_N);

	printf("多项式a_poly: ");
    print(a_poly, s_N);

	printf("output: ");
    print(a, N);

	printf("周期: %d\n", t);

    return 0;
}

运行结果为：

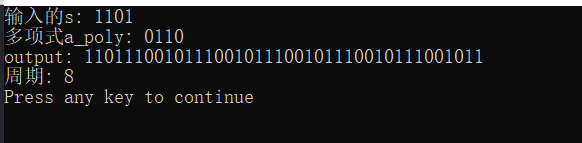
参考资料：《现代密码学 第四版》 杨波