PCA与t-SNE降维数据

PCA

主成分分析(Principal Component Analysis，简称PCA )，是常用的降维方法。PCA是一种线性的降维方法，线性变换的直观表示为：

其中，$\mathbf{x}$是原始的样本，$\mathbf{y}$是降维后的样本，$\mathbf{W}$是转换矩阵。PCA的主要目标就是求解转换矩阵，我们需要预先定义目标函数，在PCA中，有以下两个优化目标：
(1)最小化重构误差
(2)最大化投影后的方差。
最小化重构误差
有趣的是，上述两个目标能够得到等价的推导。
首先对所有样本进行中心化处理，使得${\sum }_i{\mathbf{x}}_i=0;$

上图中可以看出，左图对应为未标准化的结果，所求的投影方向不能正确反映方差最大的方向。标准化后，更能正确反映方差最大的方向。
无损转换矩阵$\mathbf{W}=({\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_d)$，${\mathbf{w}}_i$是标准正交基向量，$||{\mathbf{w}}_i|{|}_2^2=1$，${\mathbf{w}}_i^T{\mathbf{w}}_j=0(i\ne j)$。注意，在这里$\mathbf{W}$是$d$阶方阵，所以$\mathbf{W}$为正交矩阵,满足${\mathbf{W}}^T={\mathbf{W}}^{-1}$， ${\mathbf{W}}^T\mathbf{W}=I$,$\mathbf{W}{\mathbf{W}}^T=I$。$\mathbf{W}$为编码矩阵，${\mathbf{W}}^T$为解码矩阵。此时实现了无损压缩过程：
$$\begin{gathered} {\mathbf{z}}_{\mathbf{i}}={\mathbf{W}}^T{\mathbf{x}}_i编码 \\ {\hat{\mathbf{x}}}_{\mathbf{i}}=\mathbf{W}{\mathbf{z}}_i解码 \\ {\hat{\mathbf{x}}}_i=\mathbf{W}{\mathbf{W}}^T{\mathbf{x}}_i={\mathbf{x}}_i \end{gathered}$$
舍弃部分坐标向量，维度降到$d^{\prime }<d$,有损转换矩阵$\mathbf{W}=({\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_{d^{\prime }})$，则样本点${\mathbf{x}}_i$在低维坐标系中的投影是${\mathbf{z}}_i=(z_{i1},z_{i2},...,z_{i{d}^{\prime }}{)}^T$。即为编码过程：$${\mathbf{z}}_i={\mathbf{W}}^T{\mathbf{x}}_i,z_{ij}={\mathbf{w}}_j^T{\mathbf{x}}_i$$
基于${\mathbf{z}}_i$，使用转换矩阵${\mathbf{W}}^T$来重构${\mathbf{x}}_i$（注意：在这里$\mathbf{W}$不再是正交矩阵，只满足${\mathbf{W}}^T\mathbf{W}=I$,$\mathbf{W}{\mathbf{W}}^T\ne I$，所以重构后的$\widehat{{\mathbf{x}}_i}$不等于原样本${\mathbf{x}}_i$）:
$$\widehat{{\mathbf{x}}_i}=\mathbf{W}{\mathbf{z}}_i=\sum _{j=1}^{d^{\prime }}{z}_{ij}{\mathbf{w}}_j$$
原样本点与重构的样本点之间的距离为$d_i=||\mathbf{W}{\mathbf{z}}_i-{\mathbf{x}}_i|{|}_2^2$：

图中${\mathbf{l}}_i={\mathbf{z}}_i$,我们的目标是最小化$d_i$，所以误差函数的意义也表示样本点到投影方向的距离都尽量近。
$$\begin{gathered} \sum _{i=1}^m||\mathbf{W}{\mathbf{z}}_i-{\mathbf{x}}_i|{|}_2^2=\sum _{i=1}^m[(\mathbf{W}{z}_i{)}^T(\mathbf{W}{z}_i)-2{\mathbf{z}}_i^T{\mathbf{W}}^T{\mathbf{x}}_i]+const \\ =\sum _{i=1}^m{\mathbf{z}}_i^T{\mathbf{z}}_i-2\sum _{i=1}^m{\mathbf{z}}_i^T{\mathbf{W}}^T{\mathbf{x}}_i+const \\ =-\sum _{i=1}^m{\mathbf{z}}_i^T{\mathbf{z}}_i+const \end{gathered}$$
$tr(\cdot )$表示矩阵的迹，即对角线值的和。由于
$${\mathbf{z}}_i^T{\mathbf{z}}_i=tr({\mathbf{z}}_i{\mathbf{z}}_i^T)$$
带入之后可以得到：
$$\propto -tr({\mathbf{W}}^T(\sum _{i=1}^m{\mathbf{x}}_i{\mathbf{x}}_i^T)\mathbf{W})=-tr({\mathbf{W}}^T{\mathbf{X}\mathbf{X}}^T\mathbf{W})$$
此时，可以得到优化目标为：
$$\begin{gathered} \underset{\mathbf{W}}{\min }-tr({\mathbf{W}}^T{\mathbf{X}\mathbf{X}}^T\mathbf{W}) \\ s.t.{\mathbf{W}}^{\mathbf{T}}\mathbf{W}=\mathbf{I} \end{gathered}$$
最大化投影后的方差
中心思想: 寻找一个方向向量， 使得数据投影到其上后方差最大;如果能找到， 继续寻找下一个方向向量， 该向量正交于之前的方向向量， 并且尽可能保持数据方差

我们的目标是最大化投影之后的方差,即为(假设样本已中心化)：
$$\begin{gathered} \max \sum _{i=1}^m{\mathbf{z}}_i^T{\mathbf{z}}_i=\underset{\mathbf{W}}{\max }tr({\mathbf{W}}^T{\mathbf{X}\mathbf{X}}^T\mathbf{W}) \\ s.t.{\mathbf{W}}^{\mathbf{T}}\mathbf{W}=\mathbf{I} \end{gathered}$$
PCA目标函数求解
寻找$\mathbf{W}\in R^{d\times d^{\prime }}$，使得满足
$$\begin{gathered} \max \sum _{i=1}^m{\mathbf{z}}_i^T{\mathbf{z}}_i=\underset{\mathbf{W}}{\max }tr({\mathbf{W}}^T{\mathbf{X}\mathbf{X}}^T\mathbf{W}) \\ s.t.{\mathbf{W}}^{\mathbf{T}}\mathbf{W}=\mathbf{I} \end{gathered}$$
对于带有约束的优化问题，采用拉格朗日乘数法：
引入拉格朗日因子${\lambda }_i,i=1,2,...,d^{\prime }$,拉格朗日方程为：
$$\begin{gathered} L(\mathbf{W})=tr({\mathbf{W}}^T{\mathbf{X}\mathbf{X}}^T\mathbf{W})-\mathbf{\lambda }({\mathbf{W}}^{\mathbf{T}}\mathbf{W}-I) \\ \mathbf{\lambda }=diag({\lambda }_1,{\lambda }_2,...,{\lambda }_{d^{\prime }}) \\ \mathbf{\lambda }({\mathbf{W}}^{\mathbf{T}}\mathbf{W}-I)=\sum _{i=1}^{d^{\prime }}{\lambda }_i({\mathbf{w}}_i^T{\mathbf{w}}_i-1) \end{gathered}$$
由矩阵迹的性质：
$$\frac{\partial {tr(\mathbf{W}\mathbf{A}\mathbf{W}}^T)}{\partial \mathbf{W}}=2\mathbf{W}\mathbf{A},\mathbf{A}={\mathbf{A}}^T$$
令$$\begin{gathered} \frac{\partial L}{\partial \mathbf{W}}=0\Rightarrow \mathbf{X}{\mathbf{X}}^{\mathbf{T}}\mathbf{W}=\mathbf{\lambda }\mathbf{W} \\ {\mathbf{X}\mathbf{X}}^T{\mathbf{w}}_i={\lambda }_i{\mathbf{w}}_i,i=1,2,...,d^{\prime } \end{gathered}$$
${\mathbf{w}}_i,i=1,2,...,d^{\prime }$所组成标准正交基，所以可得到${\lambda }_i,{\mathbf{w}}_i$为${\mathbf{X}\mathbf{X}}^T$的特征值和特征向量。
由$$\mathbf{X}{\mathbf{X}}^{\mathbf{T}}\mathbf{W}=\mathbf{\lambda }\mathbf{W}\Rightarrow {\mathbf{W}}^T\mathbf{X}{\mathbf{X}}^{\mathbf{T}}\mathbf{W}=\mathbf{\lambda }$$
此时等价于最大化${\max }_{\mathbf{W}}tr(\mathbf{\lambda })$。此时取前$d^{\prime }$个最大的特征值对应的特征向量组成$\mathbf{W}=({\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_{d^{\prime }})$。注意，对于$n$阶协方差矩阵，其为半正定阵，即必定对应$n$个非负的特征值。由此可总结出PCA算法的一般流程:
PCA算法过程：

================================================
输入：样本集 D = { x 1 , x 2 , . . . , x m } D=\{\bm{x}_{1},\bm{x}_{2},...,\bm{x}_{m}\} D={x1​,x2​,...,xm​}和低维空间为数$d^{\prime }$
过程：
1.样本中心化：${\mathbf{x}}_i\leftarrow {\mathbf{x}}_i-\frac{1}{m}{\sum }_{j=1}^m{\mathbf{x}}_j$
2.求解样本的协方差矩阵$\mathbf{X}{\mathbf{X}}^{\mathbf{T}}$并进行特征值分解。
3.取前$d^{\prime }$大的特征值对应的特征向量${\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_{d^{\prime }}$
输出：投影矩阵${\mathbf{W}}^{\ast }=({\mathbf{w}}_1,{\mathbf{w}}_2,...,{\mathbf{w}}_{d^{\prime }})$

=============================================
在实际应用中，通常会使用SVD来求代替协方差分解：

PCA超参数确定
PCA的好处是超参数很少，只需确定低维空间的维数$d^{\prime }$即可。有如下三种方法：
（1）用户事先指定
（2）使用不同的值降维形成的样本对k近邻分类器（或者其他开销较小的分类器）进行交叉验证。
（3）设置重构阈值：
$$\frac{{\sum }_{i=1}^{d^{\prime }}{\lambda }_i}{{\sum }_{i=1}^d{\lambda }_i}\ge t$$
取特定阈值下最小的$d^{\prime }$。
优缺点分析
优点：特征向量方法；没有额外要调节的超参数，且$d^{\prime }$无局部最小值。
缺点：只用了二阶统计量（偏差和方差），不能处理高阶依赖。如所有特征向量两两独立，没有做到多个特征组合之间相互独立；只能用于线性投影。

T-SNE

PCA是一种线性降维方法，t-SNE（t-distributed Stochastic Neighbor Embedding）则是一种非线性降维方法，它将数据点的相似度转换为联合概率并优化低维数据和高维数据之间的KL误差。

SKlearn库对t-SNE函数使用：https://scikit-learn.org/stable/modules/generated/sklearn.manifold.TSNE.html?highlight=t%20sne#sklearn.manifold.TSNE

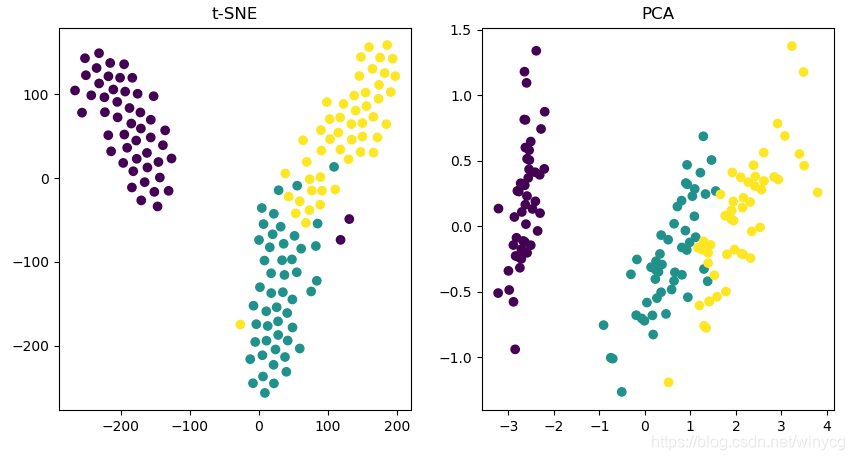
下面给出PCA和t-SNE的使用例子，对iris数据集进行降维：

from sklearn.manifold import TSNE
from sklearn.datasets import load_iris
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

iris = load_iris()
X_tsne = TSNE(learning_rate=1000.0).fit_transform(iris.data)
X_pca = PCA().fit_transform(iris.data)
plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=iris.target)
plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=iris.target)
plt.show()

t-SNE降维CIFAR-100的embeddings

给定一个预训练的分类网络，例如resnet32，提取出global average polling前的embeddings，采用t-SNE进行降维可视化：
（1）任意选取10类，提取embeddings和标签target并保存为npy文件：

import torch
import torch.backends.cudnn as cudnn

import os
import numpy as np

import models
import torchvision
import torchvision.transforms as transforms

# dataset
num_classes = 100
device = 'cuda' if torch.cuda.is_available() else 'cpu'
os.environ["CUDA_VISIBLE_DEVICES"] = '0'

testset = torchvision.datasets.CIFAR100(root=get_data_folder(),
                                        train=False, download=True,
                                        transform=transforms.Compose([
                                            transforms.ToTensor(),
                                            transforms.Normalize([0.5071, 0.4867, 0.4408],
                                                                 [0.2675, 0.2565, 0.2761]),
                                        ]))

testloader = torch.utils.data.DataLoader(testset, batch_size=1, shuffle=False,
                                         pin_memory=(torch.cuda.is_available()))

# --------------------------------------

model = getattr(models, 'resnet32')
net = model(num_classes=num_classes).cuda()
net = torch.nn.DataParallel(net)
cudnn.benchmark = True


def test():
    net.eval()
    classes = np.random.choice(np.arange(100), 10, replace=False)
    embeddings_list = []
    target_list = []
    with torch.no_grad():
        for batch_idx, (inputs, target) in enumerate(testloader):
            inputs, target = inputs.to(device), target.to(device)
            if np.sum(classes == target.item()) == 1:
                _, embeddings = net(inputs)
                embeddings_list.append(embeddings.squeeze(0).cpu().numpy())
                target_list.append(target.item())

    embeddings_list = np.asarray(embeddings_list)
    target_list = np.asarray(target_list)
    print(embeddings_list.shape)
    print(target_list.shape)
    np.save('embeddings.npy', embeddings_list)
    np.save('target.npy', target_list)

if __name__ == '__main__':
    checkpoint = torch.load('./checkpoint/' + model.__name__ + '_best.pth.tar',
                            map_location=torch.device('cpu'))
    net.load_state_dict(checkpoint['net'])
    test()

（2）从文件中提取embeddings和对应的target信息，进行t-SNE可视化：

from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np


embeddings = np.load('embeddings.npy')
target = np.load('target.npy')

X_tsne = TSNE(learning_rate=200.0, perplexity=50).fit_transform(embeddings)
X_pca = PCA().fit_transform(embeddings)

plt.figure(figsize=(10, 5))
plt.subplot(121)
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=target)
plt.title('t-SNE')
plt.xticks([])
plt.yticks([])


plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=target)
plt.title('PCA')
plt.xticks([])
plt.yticks([])
plt.show()

可以每一个类指定不同的颜色：

embeddings = np.load('baseline_embeddings.npy')
target = np.load('baseline_target.npy')

target_value = list(set(target))
color_dict = {}
colors = ['black', 'red', 'yellow', 'green', 'orange', 'blue', 'magenta', 'slategray', 'cyan', 'aquamarine']
for i, t in enumerate(target_value):
    color_dict[t] = colors[i]
print(color_dict)


X_tsne = TSNE(learning_rate=200.0, perplexity=30).fit_transform(embeddings)
plt.figure(figsize=(10, 5))

for i in range(len(target_value)):
    tmp_X = X_tsne[target==target_value[i]]
    plt.scatter(tmp_X[:, 0], tmp_X[:, 1], c=color_dict[target_value[i]])

plt.title('t-SNE')
plt.xticks([])
plt.yticks([])
plt.show()