查找算法（二分查找、顺序统计（中值））

1. 二分查找

（1）基本思想
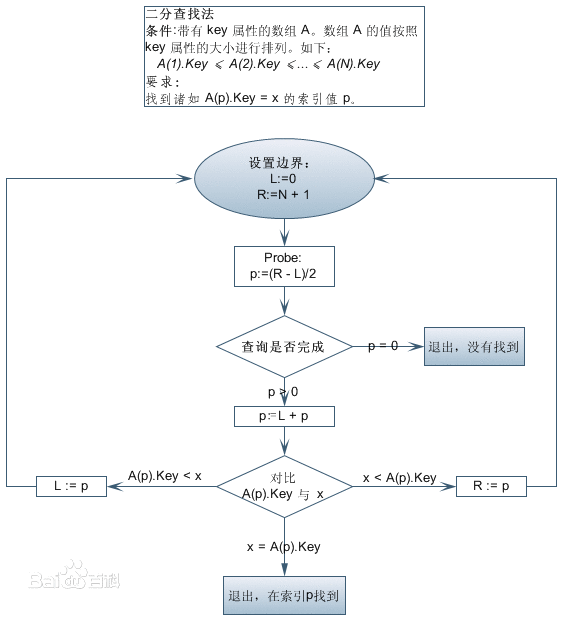
         二分查找算法的前置条件是,一个已经排序好的序列(在本篇文章中为了说明问题的方便,假设这个序列是升序排列的),这样在查找所要查找的元素时,首先与序列中间的元素进行比较,如果大于这个元素,就在当前序列的后半部分继续查找,如果小于这个元素,就在当前序列的前半部分继续查找,直到找到相同的元素,或者所查找的序列范围为空为止。

（2）自己编写的C++程序：

int Binary_search(int *a,int x,int p,int q)

{

if(a[p+(q-p)/2] == x)

{

return p+(q-p)/2;

}

else if(a[p+(q-p)/2] > x)

{

return Binary_search(a,x,p,p+(q-p)/2-1);

}

else if (a[p+(q-p)/2] < x)

{

return Binary_search(a,x,p+(q-p)/2+1,q);

}

}

2. 顺序统计（中值）

（1）基本思想（出处： http://blog.csdn.net/xiazdong）：

先来看一个问题：“给定一个无序的序列，求序列的中位数。”

正常的答案都是“先排序，再取A[n/2]，花费O(nlgn)”，学习完本文后，发现其实能够在O(n)求出中位数。

但是要注意，有些场景下前一种方法更好，比如说：“要分别求第1个顺序统计量、第二个顺序统计量、第三个顺序统计量、....、第n个顺序统计量”，如果使用“先排序后取”的方法只要 O (nlgn)，但是后一种方法，则要O(n^2)（n次select方法）。

顺序统计学要解决的问题是：“给定一个无序序列，问第k个小的数是什么？”

顺序统计学的算法是基于快速排序的partition函数，并运用了分治法的思想。

第i个顺序统计量：第i个最小的值。

本文将结合一些习题以便更好地讲解本主题。

伪代码：

最坏情况运行时间： O (n^2)

最好情况运行时间： O (1)

期望运行时间： O (n)

算法导论9.2-1中问：“对于上面的randomized_select，一定不会出现长度为0的递归调用”，因为在randomized_select中，我们的目的要求出第i个顺序统计量，因为调用randomized(A,a,b,i)，的条件是A[a,...,b]之间一定有第i个顺序统计量，因此如果调用了长度为0的数组，则与条件矛盾。

接下来要证明为什么期望运行时间是 O (n)。

(下述证明需要假设所有元素都是不相同的)

设随机变量T(n)表示select算法的运行时间，E(T(n))表示select算法的期望运行时间。

我们假设按照最坏情况来讨论，即如果划分了两个子数组后，都调用较长的那个子数组。

T(n)所有的情况如下图所示：

通过替换法即可证明E(T(n))=O(n)

而上面导致最坏情况出现的原因是randomized_partition的不确定性，怎么样能够得到一个好的划分呢？

Blum、Floyd、Pratt、Rivest、Tarjan发现了一个最坏情况还是线性时间的选择算法。

这个算法的基本思想是：每次找到的都是一个好的划分，这样就能保证select的时间是O(n)。具体细节可以看算法导论9.3节，这里我要提一些书上没有的：

(1)书上说的“分组，每组5个元素”，此处每组5个元素是最低要求，即只要大于等于5都可以，但是如果每组4个元素，则划分就不是一个好划分。

算法导论9.3-1中就需要证明如果每组3个元素，select就不是线性时间的了。

总结一句话：其实这个算法我们只要把他当做一个封装的子程序来用就可以了：“select(A,p,q,i)方法一定能够在线性时间找出A[p...q]中第i个小的元素。”

百度面试题：假设一整型数组存在若干正数和负数，现在通过某种算法使得该数组的所有负数在正数的左边，且保证负数和正数间元素相对位置不变。时空复杂度要求分别为：O(n)和O(1)

（2）自己编写的C++程序：

#include <iostream>

#include<stdio.h>

using namespace std;

int Partition(int *a,int p,int q)

{

int x = a[p];

int i = p;

int temp;

for(int j = p+1; j<=q; j++)

{

if(a[j]<=x)

{

i++;

//temp = a[i];

//a[i] = a[j];

//a[j] = temp;

swap(a[i],a[j]);

}

}

/*temp = a[p];

a[p] = a[i];

a[i] = temp;*/

swap(a[i],a[p]);

return i;

}

int Rand_Select(int *a,int p,int q,int i)

{

if(p == q)

return a[p];

int r = Partition(a,p,q);

int k = r-p+1;

if(i == k)

return a[r];

else if(i<k)

return Rand_Select(a,p,r-1,i);

else if(i>k)

return Rand_Select(a,r+1,q,i-k);

}

void main()

{

int a[7] = {9,6,4,3,2,2,10};

//Sorting

int n = sizeof(a)/sizeof(int);

for( int i=0;i<n;i++) 

cout << a[i] << " ";

cout << endl;

//Searching ith smallest

int i =4;

int key = Rand_Select(a,0,n-1,i);

cout << key << endl;

system("pause");

}