算法：动态规划入门之矩阵连乘

首先让我们复习一下矩阵连乘的有关知识。对于矩阵知识很了解的人可以跳过矩阵知识这块内容，不过笔者建议最好复习一下：

矩阵的乘法：

矩阵相乘只有在第一个矩阵的列数和第二个矩阵的行数相同時才有定义。假如A为m×n矩阵，B为n×p矩阵，则他們的乘AB(有时记做A·B)会是一个m×p矩阵。
例如一个2x3的矩阵与一个3x2的矩阵的乘会是一个2x2的矩阵 。

例子：

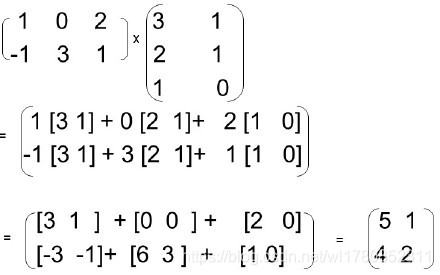
矩阵连乘：

设有矩阵M1,M2,M3,M4，
其维数分别是10×20, 20×50, 50×1 和1×100，现要求出这4个矩阵相乘的结果。我们知道，若矩阵A的维数是p×q，矩阵B的维数是q×r，则A与B相乘后所得矩阵AB的维数是p×r。按照矩阵相乘的定义，求出矩阵AB中的一个元素需要做q次乘法（及q-1次加法）。这样，要计算出AB就需要做p×q×r次乘法。为简单起见，且由于加法比同样数量的乘法所用时间要少得多，故这里我们暂不考虑加法的计算量。由于矩阵连乘满足结合律，故计算矩阵连乘的方式可以有多种。

SPAN>M1(M2(M3M4))的方式去计算，
也可以按(M1(M2M3))M4的方式去计算，所得结果是相同的。
但是值得注意的是，
按前一方式计算需要做125,000次乘法，
而按后一方式计算只需要做2,200次乘法。
由此可见，矩阵连乘的运算次序对于所需要的计算量
（所需乘法次数）有着极大的影响。
M3M4：501100=5,000；M2(M3M4)：2050100=100,000
M1(M2(M3M4))：1020100=20,000
(M2M3)：20501=1000；(M1(M2M3))：10201=200 ；
(M1(M2M3))M4：101100=1000

如何解决矩阵连乘问题：

分析：

设要求出矩阵连乘MiMi+1……Mj-1Mj（i<j）所需的最少乘法次数。
因共有j-i+1个矩阵，故称这个矩阵连乘的规模是j-i+1

按照做最后一次乘法的位置进行划分，该矩阵连乘一共可分为j-i种情况即有(j-i)种断开方式：Mi(Mi+1┅Mj)，(MiMi+1)(Mi+2┅Mj)，┅，(MiMi+1┅Mj-1)Mj。其中任一对括号内的矩阵个数（即规模）不超过j-i。若我们已知任一个规模不超过j-i的矩阵连乘所需的最少乘法次数，我们就可以很容易地计算出矩阵连乘MiMi+1┅Mj-1Mj（i<j）所需的最少乘法次数，其方法如下。将上述的j-i种情况表示为通式：(Mi┅Mk) (Mk+1┅Mj)（i≤k<j）。

记第t个矩阵Mt的列数为rt，并令rt-1为矩阵Mt的行数。
则Mi┅Mk连乘所得是ri-1×rk维矩阵，
Mk+1┅Mj连乘所得是rk×rj维矩阵，
故这两个矩阵相乘需要做ri-1×rk×rj次乘法

由于在此之前我们已知
任一个规模不超过j-i的矩阵连乘所需的最少乘法次数，故(Mi┅Mk)和(Mk+1┅Mj)所需的最少乘法次数已知，将它们分别记之为mi,k和mk+1,j。
形为(Mi┅Mk)(Mk+1┅Mj)的矩阵连乘所需的最少乘法次数为：
mi,k + mk+1,j + ri-1×rk×rj。

对满足i≤k<j 的共j-i种情况逐一进行比较，我们就可以得到
矩阵连乘MiMi+1┅Mj-1Mj（i<j）所需的最少乘法次数mi,j为：
mi,j=min { mi,k + mk+1,j + ri-1×rk×rj } （i≤k<j）

于是在初始时我们定义mi,i=0（相当于单个矩阵的情况）
求m1,2：即i=1, j=2，
就是2个矩阵，无需划分 (k=1,因为i<=k<j)
m1,2=min{ m1,1 + m2,2 + ri-1×ri×ri+1
=ri-1×ri×ri+1=r0×r1×r2= 10×20×50=10000，
求m23：即i=2, j=3，故ri-1×ri×ri+1=r1×r2×r3=20×50×1=1000，
求m13：即i=1, j=3，min（i≤k<j）{mik+mk+1,j+ri-1×rk×rj}=
min{ (m11+m23+r0×r1×r3)(k=1)，(m12+m33+r0×r2×r3)(k=2)}=
min{(0+1000+200), (10000+0+500)}= min{1200,10500}=1200

矩阵在C语言中的表示方法：

A[i][j] (i为行，j为列)

拥有了上面的准备知识看下面的内容就会轻松很多。

注：下文所用的mi,j或者m[i][j]表示MiMi+1┅Mj-1Mj（i<j）所需的最少乘法次数

首先，让我们自己思考一下怎么解决一个n个矩阵连乘的问题，也许有了上面的知识你会想到下面的递归的方法：

假设已经算好了Mi┅Mk和Mk+1┅Mj这两个子矩阵各自相乘的最小的次数，剩下的只需要算最后一次乘积的次数就可以了，也就是这里的两个子矩阵相乘所涉及的乘法次数ri-1×rk×rj然后加上前面所得的两个子矩阵各自所需的最小的相乘次数就可以了。这样就得到了上面所说的这个式子：mi,j = mi,k + mk+1,j + ri-1×rk×rj 然后依次判断在k等于某个数的时候所得的mi,j的值，剩下的只需要对所有的mi,j的值取一个最小值就ok了，于是我们就得到了上面所说的这个式子： mi,j=min { mi,k + mk+1,j + ri-1×rk×rj } （i≤k<j）
然而这样做并不能求出mi,j的最小值，因为我们不知道 mi,k 和 mk+1,j的值。但是，这并不会难倒我们，因为我们知道对于 mi,k 和 mk+1,j 的求解可以基于递归思想。方法和求解mi,j的最小值一样。这样我们就得到了递归的式子：

下面代码的p[i]表示的是第i个矩阵的列数，当然他的行数就用i-1表示，呵呵。
int min(int a,intb){
return a<b?a:b;
}
int d(int i,int j){
int i,j,k,t,u;
if(ij) return 0; //ij时就是mi,i，也就是单个矩阵，当然，单个矩阵不存在乘积所以为0
if(i==j-1) return p[i-1]*p[i]*p[j]; //明显，这是相邻的两个矩阵的乘积
u=d(i,i)+d(i+1,j)+p[i-1]*p[i]*p[j]; //1
for(k=i+1;k<j;k++){ //2
t=d(i,k)+d(k+1,j)+p[i-1]*p[k]*p[j]; //2
u=min(t,u); //3
}
}

1 对于从矩阵i到矩阵j的连乘，当k==i时所得的mi,j
2 对于从矩阵i到矩阵j的连乘，当i<k<j时所得的 mi,j
注：1 ， 2 所说的结合起来就是 3 也就是上面蓝字部分的分析
3 就是mi,j=min { mi,k + mk+1,j + ri-1×rk×rj } （i≤k<j）

可是，有兴趣的话你可以算一下用递归做的效率，你会发现，复杂度是O(2^n)，这个复杂度太大了，稍大一点的数据就爆了不仅timelimitexceeded而且也会memorylimitexceeded，所以我们就必须换一种方法改用dp(动态规划)，但是，我们的思路还是一样的，换句话说，只不过把递归的形式改为dp的形式而已，没什么新的东西，如果说有的话也只是记录了中间状态。请看下面的代码：

int dp_matrix_multiply(){
int i,j,r,k,tem;
n-=1;
for(i=1;i<=n;i++) //1
m[i][i]=0; SPAN>
for(r=2;r<=n;r++){ //2
for(i=1;i<=n-r+1;i++){ //3
j=i+r-1; //3
m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j]; //4
for(k=i+1;k<j;k++){ //4
tem=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j]; //4
m[i][j]=tem<m[i][j]?tem:m[i][j]; //4
}
}
}
return m[1][n];
}

初看，是不是很头痛？？我刚开始接触的时候看到别人这么写也很头大，但是思考了近3个小时后终于理解了。

首先我们看一下注释1，这部应该很好理解吧，就是初始化单个矩阵连乘的最小次数，当然单个矩阵不可能与其自身相乘所以赋值为0

然后是注释2，这个我想应该是初学者最难以理解的地方之一了吧(包括当时的我也一样,呵呵)，其实这里的r就是 the matrix train length，连乘的矩阵个数。这里从2开始，有两个原因：首先单个矩阵的乘积(就是其自身，这一步已经在1中阐明了)已经初始化好了，也就是说我们已经求得了r1时的若干单个矩阵最小的乘积次数，接下去当然要求r2时，若干个由两个矩阵组成的的子矩阵乘积的最小的次数，然后依次类推。其次，对于这里的r的解释我们可以看一下这个状态方程： mi,j=min { mi,k + mk+1,j + ri-1×rk×rj } （i≤k<j）
如果我们要知道mi,j的值，我们就必须知道 mi,k 和 mk+1,j的值，而mi,k和mk+1,j的求解又是通过更小的子模块来实现，以此类推最后在mi,i，也就是单个矩阵的地方终止子问题的进一步求解，因为没有比单个矩阵更小的子问题了，讲到这里我们不妨抽点时间再看一下上面讲的递推的方法，你会发现递归的实质就是求解更小的子模块，这不是和这里的dp求解子模块的方法一样吗。而且你会发现，注释4的部分和递归求解的2，3部分几乎一模一样，那是不是同样的意思呢，相信自己吧，你理解的是正确的，但是，你要注意一下dp的方法优越于递归的方法的主要原因就是将递归中的t=d(i,k)+d(k+1,j)+p[i-1]*p[k]*p[j];改成了tem=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];这样用数组记录状态节约了大量的时间，因为递归方法中d(i,k)这个函数总是被多次调用，不能用递归的方法解决大数据的原因就在于此。

理解了上面的内容注释3的意思也不难看懂了，i和j就是MiMi+1┅Mj-1Mj（i<j）中的i和j，至于i的值为什么从1到n-r+1以及j的值为什么是i+r-1不用我说你也应该理解，i从1到n-r+1就是r个矩阵连乘的第一个矩阵的下标(注：这里矩阵的下标从1开始),既然这样那么j就是r个矩阵相乘最后那个矩阵的下标。





如下图，如果我们使用递归，则会产生大量的重复计算，复杂度太高，当然使用备忘录降低复杂度。不过更好的是使用递推




图4：

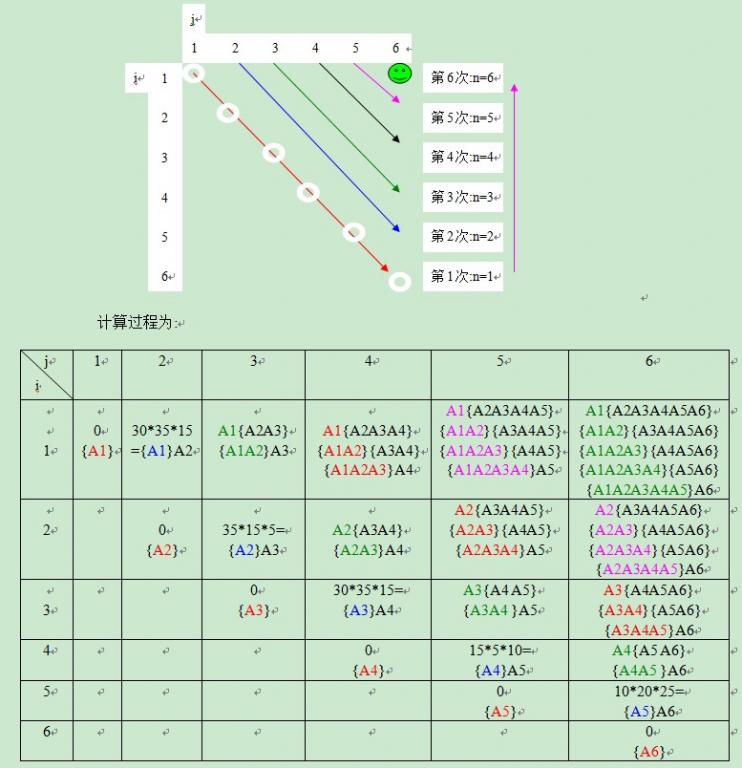
C++实现如下：

#include<bits/stdc++.h>
using namespace std;
void matrixChain(int n,int p[],int m[][100],int s[][100])//递推
{
	for(int i=1; i<=n; i++) //对角线先为0
	{
		m[i][i]=0;
	}
	for(int r=2; r<=n; r++) //一共n-1个对角线 对角线个数
	{
		for(int i=1; i<=n-r+1; i++) //第i行
		{
			int j=i+r-1;//在该行的对角线上的点对应的j值
			m[i][j]=m[i+1][j]+p[i-1]*p[i]*p[j];//初始化此时在i处取得最优解（对角线长度最左边断开一个矩阵次数为 0所以省去不写）
			s[i][j]=i;//从i处断开
			for(int k=i+1; k<j; k++) //如果有更小的则被替换
			{
				int t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];//计算图4中i=1，j=3第二行类似的连乘次数 
				if(t<m[i][j])
				{
					m[i][j]=t;
					s[i][j]=k;
				}
			}
		}
	}
}
void print_optimal_parents(int s[100][100],int i,int j)//打印划分的结果
{
	if( i == j)
		cout<<"A"<<i;
	else
	{
		cout<<"(";
		print_optimal_parents(s,i,s[i][j]);
		print_optimal_parents(s,s[i][j]+1,j);
		cout<<")";
	}

}
int main()
{
	int p[1000];//每个矩阵的行数和最后一个的列数
	int m[100][100];//存储最优子结构
	int s[100][100];//存储当前结构的最优断点
	memset(p,0,sizeof(p));
	memset(m,0,sizeof(m));
	memset(s,0,sizeof(s));
	cout << "请输入矩阵的个数"<< endl;
	int n;
	cin >> n;
	cout << "请依次输入每个矩阵的行数和最后一个矩阵的列数"<< endl;
	for(int i=0; i<=n; i++)
	{
		cin >> p[i];
	}
	matrixChain(n,p,m,s);
	cout <<"这些矩阵相乘的最少次数是"<<m[1][n]<<endl;

	cout<<"结果是:"<<endl;
	print_optimal_parents(s,1,n);
	return 0;
}

结果：

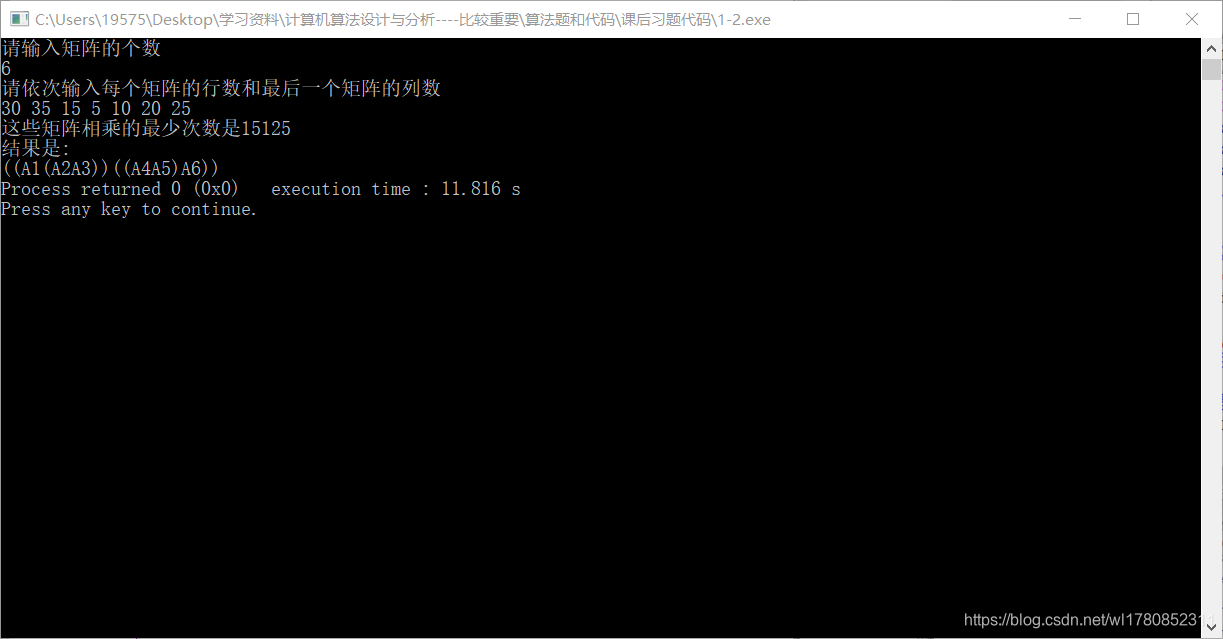
呼~~~~，至此完毕，终于弄懂了矩阵连乘问题