注:该算法已按照智能优化算法APP标准格式进行整改,可直接集成到APP中,方便大家与自己的算法进行对比。
H5N1优化算法受到禽类和人类中H5N1禽流感病毒感染机制及其变异机制的启发,可以通过模拟H5N1病毒的适应性行为和进化过程来探索优化问题的最优解,从而提升算法在各种优化问题中的性能,该算法提出了一种基于感染概率的平衡随机概率机制,借助该机制,H5N1算法可以改变其迭代阶段。
该成果于2025年最新发表在2区计算机领域期刊Engineering Computations上。

H5N1是一种甲型流感病毒亚型,该病毒具有一层脂质膜,包裹着一层蛋白质,称为血凝素( ),以及另一层蛋白质,称为神经氨酸酶( )。 和 是病毒的表面蛋白,在病毒侵入和传播人类及动物体内的过程中起着重要作用。H5N1的形态如下图所示。
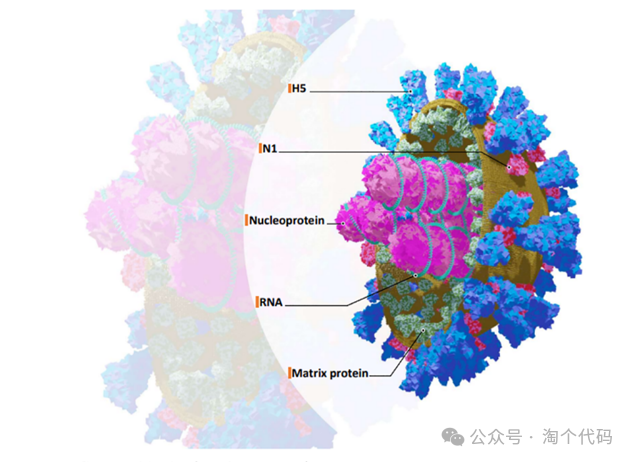
H5N1病毒独特且强大的特性,尤其是其快速传播、突变和环境适应能力,为H5N1算法提供了灵感。与当前通常模拟相对静态自然过程(如遗传进化或群体行为)的生物启发算法不同,H5N1算法利用了病毒的适应性和动态特征。
1.算法原理
为建立H5N1病毒的数学表示,首先将受病毒影响的种群划分为两个不同的群体:家禽与人类。H5N1 病毒主要通过感染家禽和牲畜传播,再通过与禽类及其排泄物、受污染的家庭用品或食物,以及感染者的直接接触,以较低的传播率传播给人类。
类似于其他元启发式技术,H5N1 病毒位于一个 维( )搜索空间中,其中 表示变量数量,所有病毒的位置由一个二维矩阵表示,记作 。
H5N1 病毒的移动和新位置的探索由多个参数引导,如向家禽或人类的传播率,用参数 表示。生存参数 用于评估宿主的免疫反应:若宿主免疫力强,病毒将发生突变以生成更适应宿主的新毒株;若宿主免疫力弱,则病毒将在H5N1病毒种群中调整其位置。
此外,病毒的目标宿主(如家禽或人类)用 表示,代表搜索空间中的全局最优解;而每个病毒群体的局部最优解用 表示。因此,H5N1 算法可作为描述病毒传播并优化控制策略的模型。
如前所述,当宿主死亡或环境不利时,病毒具备变异能力。因此,需构建一个模拟病毒在逆境中突变的数学表达式。为此,本文提出了一种基于对病毒种群中最优位置进行置换的变异方法。通过这种置换方式,算法能更有效地在种群中探索与利用最优位置,而非仅依赖单一全局最优,从而避免陷入局部最优。
本文提出的置换方法通过以下公式给出:
其中 是从区间 中的随机整数。根据偏移量 对数组 中的索引进行旋转,以计算向量 :
其中
通过根据数组 移动数组 中的索引来创建数组 ,其中每个元素递增 个单位:
通过基于移位 旋转数组中的索引来计算数组 :
通过根据数组 移动数组 中的索引来创建数组 ,其中每个元素递增 个单位:
根据数组 、 和 中的索引,从矩阵 中提取相应的行,以生成三个矩阵 、 和 。
提出了一种替代公式,用于调整病毒的位置,可用于模拟H5N1病毒在人群中的行为:
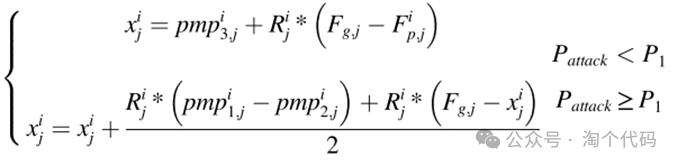
如果病毒攻击家禽的概率(记作 )小于 ,则使用包含第 次置换种群 、全局最优位置 、局部最优位置 和包含随机数 的矩阵 的公式来更新病毒位置。否则,若 ,则病毒位置使用包含当前位置 、第 次与第 次置换种群 、 和 的公式进行更新。
由于病毒在家禽种群中传播迅速, 通常取值为 到 之间以获得最佳结果。因此,当攻击家禽时,感染率 会更高,需要一个公式帮助病毒在种群中快速且精准地感染个体;当 时,病毒被引导朝向种群中最优值的方向进化。
尽管已在公式中有效地捕捉了病毒对宿主的攻击行为,但尚未在数学上建模病毒在家禽与人类环境中应对不利条件时如何发生变异。因此,需要一个能够刻画病毒变异特性的公式,如下所示的公式:
在公式中, 表示 的先前位置, 表示在半径为 的范围内搜索到的 的新位置, 表示病毒在变异后的位置信息。 是基于 与 的均值计算而得,并引入了随机性与加权机制以确保收敛性。
为描述病毒所处的环境及其所面临的挑战,使用了两个参数: 和 。其中, 是一个随机参数,用于表征病毒的适应能力; 表示宿主在感染后的存活概率,或病毒的变异率,即病毒的适应概率。
若 ,表示当前环境有利于病毒生长,则使用公式进行计算;反之,若 ,说明环境不利,病毒需通过变异进行适应。
SH5N1中最重要的参数之一是权重系数w,它保持了对病毒的利用。其定义如下:
其中, 表示第 次迭代, 为最大迭代次数。变量 表示权重因子, 为权重的阻尼系数, 和 分别表示权重的最小值和最大值。
此外,参数 起着关键作用。它通过公式计算,用于管理病毒的状态,在“ ”(即搜索新的可能性)与“ ”(即利用已知资源)之间寻求平衡,从而防止由于权重因子 的影响导致算法过于偏重开发。
如下图所示, 在整个计算过程中呈现均匀分布。
这张图描绘了p和c的分布。可以观察到,pi是平衡的,因为它在算法的前半部分从0均匀地分布到1。这导致在初始阶段容易选择xmutate突变。然而,在下半部分,分布变得更加集中并更接近1,这使得对探索搜索空间的重视程度降低。这是避免算法过度关注开发的重要因素,这在扩展搜索空间方面是有利的。
此外,由于突变并不总是产生有利的结果,因此需要一个系数来控制病毒的适应性。其方程式如下所示:
上述方程包括控制病毒突变后适应性的参数p和0至1之间的随机参数r5。这里的目的是根据迭代次数来控制变异后病毒的适应性。
在更新到全局最佳值之前,病毒的当前位置将按照以下方式更新:
其中mx为当前病毒的变异系数向量,在α3的置换条件下,该向量将用随机系数的随机向量进行更新,mxp为病毒群体的变异系数向量。
最后,将使用随机机制用全局最佳解更新算法,如以下等式所示:
H5N1算法以生成一组随机的初始解(即病毒种群)作为起点。随着算法在迭代过程中不断推进,它通过在“ ”与“ ”阶段之间随机切换,持续逼近最优解的可行位置。
为了调节探索与开发之间的平衡,算法引入了参数 和 ,其中 从 递减至 , 则从 递增至 。此外,引入参数 用于控制变异,其数值从 递减至 ,以限定变异范围,并有选择地保留对结果有积极贡献的值,而非不加筛选地接受所有变异值。
当满足预设终止条件后,H5N1 算法结束运行。算法 给出了H5N1算法的伪代码,而下图则展示了H5N1整体流程的详细图示。
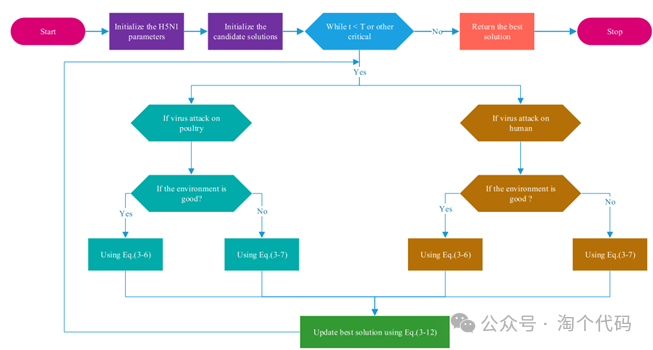
H5N1优化算法的伪代码如下所示:

2.结果展示
23个经典函数结果:





3.MATLAB核心代码
%% 淘个代码 %%
% 微信公众号搜索:淘个代码,获取更多代码
% H5N1优化算法
function [GlobalBest_Cost, GlobalBest_Position, BestCosts] = SH5N1(nvirus, Max_iter, lb, ub, dim, ObjectiveFunction)
% SH5N1 - Metaheuristic optimization algorithm
% [GlobalBest_Cost, GlobalBest_Position, BestCosts] = SH5N1(nvirus, Max_iter, lb, ub, dim, ObjectiveFunction)
% Inputs:
% nvirus: size of the virus population
% Max_iter: maximum number of iterations
% lb: lower bounds for decision variables
% ub: upper bounds for decision variables
% dim: number of variables
% ObjectiveFunction: handle to the function that computes the cost of a candidate solution
% Outputs:
% GlobalBest_Cost: cost of the best solution found
% GlobalBest_Position: decision variable values of the best solution found
% BestCosts: vector containing the cost of the best solution in each iteration
if size(lb,2) == 1
lb = repmat(lb,1,dim);
ub = repmat(ub,1,dim);
end
% setting up parameter for H5N1 algorithms
P1 = 0.8; % Probability of attaching to a bird, poultry
P2 = 0.85; % Probability of survival after infection
w = 1;
wmin = 0.001;
wmax = 1;
p = 0;
m_virus = zeros(nvirus,dim); % mutate for virus virus population
m_virusBest = zeros(nvirus,dim); % mutate for virusBest virus population
ro = (0:1:nvirus-1); % rotating index array
R = rand(nvirus,dim); % matrix of normalization random number for all
v = rand(nvirus,1); % vector of normalization random number for mutate
%% Initialize the virus population randomly
virusCost = zeros(nvirus,1); % cost of virus of virus
virusPosition = zeros(nvirus,dim); % position of virus of virus
virusBestPosition = rand(nvirus, dim).*(ub-lb) + lb; % initilization first virus population
virusBestCost = zeros(nvirus, 1);
% Evaluate the objective function for each individual
for i = 1:nvirus
virusBestCost(i) = ObjectiveFunction(virusBestPosition(i, :));
end
% Find the best individual
[GlobalBest_Cost, bestidx] = min(virusBestCost);
GlobalBest_Position = virusBestPosition(bestidx, :);
%% value store for visualization
BestCosts = zeros(Max_iter,1); % save best solution of every iteration
%% Main loop
for iter = 1:Max_iter
c = exp(-4*iter/Max_iter)*rand(); % Eq. 3-9
p = 1 ./ (1 + exp(-10*(iter/Max_iter-0.5))) + rand()*(1-p); % Eq. 3-10 Multation probability
wd = wmin + (wmax-wmin)*exp(-(iter/Max_iter)); % Eq. 3-8 (part 2)
% Determine the probability of attaching to a bird
P_attack = rand(nvirus, 1);
% Determine the probability of survival after infection
P_adapt = rand(nvirus, 1);
sigma = randperm(3); % index pointer array
a1 = randperm(nvirus); % Eq. 3-1
rt1 = rem(ro+sigma(1),nvirus); % Eq. 3-2
a2 = a1(rt1+1); % Eq. 3-3
rt2 = rem(ro+sigma(2),nvirus); % Eq. 3-4
a3 = a2(rt2+1); % Eq. 3-5
pmp1 = virusBestPosition(a1,:); % permutate virus population 1
pmp2 = virusBestPosition(a2,:); % permutate virus population 2
pmp3 = virusBestPosition(a3,:); % permutate virus population 3
v = v(a3,:); % permutate coefficient
sm = rand(nvirus,dim); % stochastic for mutate
% Update the virus population using the infected fitness
for i = 1:nvirus
m_virus(i,:) = sm (i,:) < v(i,1); % all random numbers < vm are 1, 0 otherwise
m_virusBest(i,:) = m_virus (i,:) < v(i,1); % inverse mutate virus to virusBest
% Move the individual according to the probability of survival
% Check if the virus attaches to poultry or human
if P_attack(i) < P1 % attach to poultry
% Calculate the probability of survival of the poultry
if P_adapt(i) < P2 % Good enviroment / the poultry will survives
% Get direction
direction = GlobalBest_Position - virusBestPosition(i,:);
virusPosition(i,:) = pmp3(i,:)+ R(i,:).*direction; % Eq. 3-6 (part 1)
else % Bad enviroment / the poultry will not survive
xold = GlobalBest_Position ; % Eq. 3-7 (part 1)
xnew = virusPosition(i,:) + R(i,:).*(GlobalBest_Position-virusPosition(i,:)); % Eq. 3-7 (part 2)
virusPosition(i,:) = 1/2*c*w*(xnew+xold)*rand(); % Eq. 3-7 (part 3)
virusCost(i) = ObjectiveFunction(virusPosition(i,:));
ps = rand();
% Update the global best position and cost Eq. 3-12
if ps < p && virusCost(i) < GlobalBest_Cost
GlobalBest_Position = virusPosition(i,:);
GlobalBest_Cost = virusCost(i);
end
end
else % attack to human
if P_adapt(i) < P2 % Good enviroment /the human will survives
% Get direction
direction = GlobalBest_Position - virusBestPosition(i,:);
virusPosition(i,:) = virusPosition(i,:) + (R(i,:).*(pmp1(i,:)-pmp2(i,:)) + R(i,:).*direction)/2; % Eq. 3-6 (part 2)
else % Bad enviroment / the human will not survive
xold = GlobalBest_Position ; % Eq. 3-7 (part 1)
xnew = virusPosition(i,:) + R(i,:).*(GlobalBest_Position-virusBestPosition(i,:)); % Eq. 3-7 (part 2)
virusPosition(i,:) = 1/2*c*w*(xnew+xold)*rand(); % Eq. 3-7 (part 3)
virusCost(i) = ObjectiveFunction(virusPosition(i,:));
ps = rand();
% Update the global best position and cost Eq. 3-12
if ps < p && virusCost(i) < GlobalBest_Cost
GlobalBest_Position = virusPosition(i,:);
GlobalBest_Cost = virusCost(i);
end
end
end
end
% Mutate
virusPosition = virusPosition.* m_virus + virusBestPosition.* m_virusBest; % Eq. 3-11
%% CheckBoundary / Clip the position to the search space
changeRows = virusPosition > ub;
virusPosition(changeRows) = pmp1(changeRows);
changeRows = virusPosition < lb;
virusPosition(changeRows) = pmp2(changeRows);
% Evaluate new position
for i = 1:nvirus
virusCost(i,:) = ObjectiveFunction(virusPosition(i,:)); % check cost of competitor
end
% Update for virusBest and Globalbest Eq. 3-12
for i = 1:nvirus
if (virusCost(i) <= virusBestCost(i))
virusBestPosition(i,:) = virusPosition(i,:);
virusBestCost(i) = virusCost(i);
if (virusBestCost(i) <= GlobalBest_Cost)
GlobalBest_Cost = virusBestCost(i);
GlobalBest_Position = virusPosition(i,:);
end
end
end
w = w * wd; % Eq. 3-8 (part 1)
BestCosts(iter) = GlobalBest_Cost;
if (mod(iter, 1) == 0)
fprintf('The best solutions at iteration %4.0f is: %3.12f \n',iter, GlobalBest_Cost)
end
end4.参考文献
参考文献 :Le T X, Bui T T, Tran H N. The H5N1 algorithm: a viral-inspired optimization for solving real-world engineering problems[J]. Engineering Computations, 2025.
本期算法代码获取
后台回复关键词:
TGDM843
获取更多代码:

或者复制链接跳转:https://docs.qq.com/sheet/DU3NjYkF5TWdFUnpu























 2942
2942

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










