让移动更自然——缓动公式原理研究

介绍：

制作游戏时，经常会遇到一些物体移动的需求。如果只是让物体直接出现在目标地点会显得非常突兀且单调。也可以使用匀速移动，让效果更平滑一点。这里我介绍一个非常平滑且自然的效果公式（每帧调用）：

其中，y为要控制的量，比如坐标，b是目标点，c是参数，一般在（0，1）之间。

通俗的理解，就是让物体距离是上一次距离的若干比例倍。

效果图：

实际使用效果

逐帧观察：

逐帧效果

特点

1.开始时移动很快，能给人直接的反馈（发出命令后立即相应），交互感强。

2.然后，在逼近过程中，随着移动，速度慢慢变小，移动变慢，

3.最后当无限接近目标（但不会完全到达，是无限趋紧关系）时，速度接近0，看起来就像是自己慢慢停下来了。最终速度为0，非常自然。

可见，该动画效果很好，实际使用很广泛。

该公式的计算也很简单，只需一次减法与一次乘法，效率高。

 

实际使用时一般通过一个bool值控制，当几乎完全到达后就不再执行其中的计算。

另外会再乘Time.deltaTime;好减少它的移动随帧数的影响

实际应用举例：

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Smooth : MonoBehaviour {

    public Transform target;
    public float smooth=0.2f;
    public bool isSmooth=true;
	
	// Update is called once per frame
	void Update () {
        if (isSmooth)
        {
            transform.position += (target.position - transform.position) * smooth* Time.deltaTime;
            if ((target.position - transform.position).magnitude < 0.001f)
            {
                transform.position = target.position;
                isSmooth = false;
            }
        }

    }
}

关键语句

transform.position += (target.position - transform.position) * smooth* Time.deltaTime;

下面通过数学推导来分析：

中每帧计算y的改变量，相当于在趋紧数学中的微分（就是计算间隔很小，当间隔无限小时该公式趋近于数学微积分）一般每帧调用，也就是说t的改变量已经很小，效果接近于微积分结果。我们把它抽象成数学模型：

即

这是一个一阶线性微分方程，高等数学中有关于它的求解：

一阶线性微分方程

的通解为

为了研究方便，我们假设开始时初位置是0.即：x=0时，y=0

由此解出

将y和y’带入原方程，成立，验证通过

用matlab画出了这个函数的图像：

（其中b=1，c=0.05）

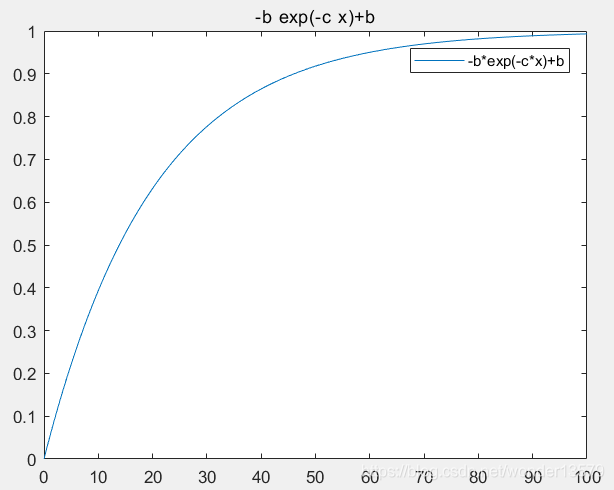
y的图像

可见它的性质与之前讨论的一样。它最后会趋近于常量b。

它的导函数图像：

y’的图像

可见其速度慢慢减少到0。

由于这是一个完全的数学问题，该模型与实际符合的极好，从中也可以看到实际效果的图像。

从结果看，这个简单的公式实际表达式的计算非常复杂，但是只用一个简单的

就产生了一样的效果，既简洁又高效。也许这就是数学的魅力吧！