Java判断一个整数是否是 2 的幂次方及应用场景

        判断一个整数是否是 2 的幂次方，具体来说，这个方法的核心思想是：如果一个数是2的幂次方，那么它的二进制表示中只有一个1，其余都是0。例如，2的幂次方有：1 (2^0), 2 (2^1), 4 (2^2), 8 (2^3) 等等，下面将详细进行原理分析、举例说明及Java代码实现。

一、原理分析

   1. 2 的幂次方特性：

•   二进制表示中，2 的幂次方的数只有 1 个二进制位为 1，其余位为 0。
  • =1 : 0001 (二进制)
  • =2 : 0010
  • =4 : 0100
  • =8 : 1000
• 通常我们称这种特性为“只有一个 1”。

---

二、举例说明

示例 1：输入 val = 8()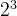

• val = 8，二进制：0000 1000
• -val 的二进制：
  • 8 的取反：1111 0111
  • 加 1 得到 -8：1111 1000
• 计算 val & -val：

0000 1000  (val)
&
1111 1000  (-val)
--------
0000 1000  (结果)

• 结果为 val 本身，8 是 2 的幂次方。

---

示例 2：输入 val = 6（非 2 的幂次方）

• val = 6，二进制：0000 0110
• -val 的二进制：
  • 6 的取反：1111 1001
  • 加 1 得到 -6：1111 1010
• 计算 val & -val：

  0000 0110  (val)
  &
  1111 1010  (-val)
  --------
  0000 0010  (结果)

• 结果为 2，不等于 6，所以 6 不是 2 的幂次方。

---

示例 3：输入 val = 1 ()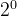

• val = 1，二进制：0000 0001
• -val 的二进制：
  • 1 的取反：1111 1110
  • 加 1 得到 -1：1111 1111
• 计算 val & -val：

0000 0001  (val)
&
1111 1111  (-val)
--------
0000 0001  (结果)

• 结果等于 val 本身，1 是 2 的幂次方。

---

三、Java实现

 private static boolean isPowerOfTwo(int val) {
        return (val & -val) == val;
 }

1. 位运算 (val & -val)：

• -val 是 val 的二进制取反加一（即补码表示）。
• 位运算 val & -val 的结果是：保留 val 中最右边的 1，其他位清零。

2.判断 (val & -val) == val：

• 如果 val 是 2 的幂次方，则 val 的二进制中只有一个 1。
• 在这种情况下，val & -val 的结果必然等于 val 本身。
• 如果 val 不是 2 的幂次方，val 中会有多位 1，此时 val & -val 的结果不等于 val。

以上代码利用了二进制的特点：

• (val & -val) 提取 val 中最右边的 1。
• 如果结果等于 val 本身，则说明 val 是 2 的幂次方。

四、应用场景

1.2幂次方按位与获取数组下标

        在一些高效的 轮询调度 或 负载均衡的获取下标元素时如果是2的幂次方效率会更高，适合在多线程环境下将任务分发给一组固定的 EventExecutor，例如 Netty 的线程模型，Netty中优先使用2幂次方按位与从数组中获取每个EventExecutor执行器，在高并发情况下比取模运算性能好。

    private static final class PowerOfTwoEventExecutorChooser implements EventExecutorChooser {
        private final AtomicInteger idx = new AtomicInteger();
        private final EventExecutor[] executors;

        PowerOfTwoEventExecutorChooser(EventExecutor[] executors) {
            this.executors = executors;
        }

        @Override
        public EventExecutor next() {
            return executors[idx.getAndIncrement() & executors.length - 1];
        }
    }

• 轮询机制：每次调用 next()，通过idx.getAndIncrement() 实现了不断递增的索引，通过按位与操作，将索引映射到 [0, executors.length - 1] 范围，依次返回 executors 数组中的下一个元素。
• 高性能场景：2的幂次按位与操作比模运算（%）更高效，位运算确保了即使 idx 无限增大，索引计算依然高效、无溢出问题。

2.取模获取数组下标

        如果数组长度为任意值（不是 2 的幂）的情况，那么就要用到取模运算，比如Netty中也提供了取模算法从数组中获取每个EventExecutor执行器

   private static final class GenericEventExecutorChooser implements EventExecutorChooser {
        // Use a 'long' counter to avoid non-round-robin behaviour at the 32-bit overflow boundary.
        // The 64-bit long solves this by placing the overflow so far into the future, that no system
        // will encounter this in practice.
        private final AtomicLong idx = new AtomicLong();
        private final EventExecutor[] executors;

        GenericEventExecutorChooser(EventExecutor[] executors) {
            this.executors = executors;
        }

        @Override
        public EventExecutor next() {
            return executors[(int) Math.abs(idx.getAndIncrement() % executors.length)];
        }
    }

从 AtomicLong 的 idx 中获取当前值，并原子性地将其递增 1，对 idx 的值取模，确保索引始终在 [0, executors.length - 1] 的范围内，Math.abs() 将其转换为正值，即便数组长度不是 2 的幂,也能计算出索引从 executors 数组中选择对应的 EventExecutor 并返回。

3. 2的幂次方和取模运算对比

 1. 2的幂次方位运算

• 位运算更高效，在二进制层面操作，按位与（&）是对每一位进行布尔与操作，直接由硬件支持，通常在一个 CPU 时钟周期内完成，效率极高。按位运算复杂度为 O(1)，固定时间完成。
• 要求位运算数必须是 2 的幂

  2. 取模运算

• 更通用，支持任意数组长度。
• 性能稍低于按位与操作，取模涉及整数除法运算，需要计算商和余数。除法操作在硬件中比加法、位移操作复杂得多，通常需要多个时钟周期才能完成。

五、总结

因此，通过这种简单的位运算方法可以有效地判断一个数是否是2的幂次方，避免了循环或递归判断，效率非常高。优先使用2的幂次方这种优化在高并发场景 和 性能敏感系统 中非常有用，例如选择数组索引、任务分发等。

• 按位运算更快，因为：
  • 它直接操作二进制位，按位与（&）操作的结果是保留两个数的二进制位都为 1 的部分。
  • 在硬件层面支持高效执行。
• 使用场景：
  • 当模数是 2 的幂时，使用按位与操作代替取模可以显著提高性能。
  • 如果模数不是 2 的幂，则必须使用传统的取模运算。
• 应用场景
  • 高效的轮询任务分发、线程池选择、负载均衡器等。

• 为什么需要 2 的幂？

  • 只有 2 的幂次方的数组长度，才能通过 & (length - 1) 计算出合法的数组下标。
  • 这是因为 2 的幂次方的减 1 的二进制掩码能精确限制范围。