2024年Python最新Python实现Gauss-Seider迭代法（超全）

def matvec(A,v):

M,N = A.shape

if N != M:

print(“Matrix is not square”)

return -1

N1 = v.shape[0]

if N1 != M:

print("The dimension of matrix and vector is not reasonable ")

result = np.zeros((N1,1),dtype = np.float32)

for i in range(N):

for j in range(N):

result[i] += A[i,j]*v[j]

return result

def product(v1,v2):

result = 0

M,N = v1.shape[0],v2.shape[0]

if N != M:

print(“The dimension of vectors is not reasonable”)

exit(1)

for i in range(M):

result += v1[i]*v2[i]

return result

def vecnorm2(v1):

N = v1.shape[0]

result = 0

for i in range(N):

result += v1[i]*v1[i]

result = np.sqrt(result)

return result

def cgsolver(A,b,x0,maxit:int,tol=1.0e-8):

if tol < 0:

print(“argument tol is not good (negitive)”)

if maxit <= 0:

maxit = 1000

xk = x0

rk = b-matvec(A,xk)

dk = rk

for i in range(maxit):

print(“iteration:{}, norm(x)= {}, norm(rk) = {}”.format(i, vecnorm2(xk),vecnorm2(rk)))

if vecnorm2(rk) <1.0e-16:

print(“A good approximation solution is obtained”)

return xk

Adk = matvec(A,dk)

alphak = product(rk,rk)/product(dk,Adk)

xkp = xk + alphak*dk

res = xkp-xk

if vecnorm2(res) < tol:

print(“A good approximation solution is obtained”)

return xk

xk = xkp

rkTrk = product(rk,rk)

rk = rk -alphak*Adk

betak = product(rk,rk)/rkTrk

dk = rk + betak*dk

print(“Max iteration reachs”)

return xk

def cgsolver1(A,b,x0,maxit:int,tol=1.0e-8):

if tol < 0:

print(“argument tol is not good (negitive)”)

if maxit <= 0:

maxit = 1000

xk = x0

rk = b-np.matmul(A,xk)

dk = rk

for i in range(maxit):

print(“iteration:{}, norm(x)= {}, norm(rk) = {}”.format(i, np.linalg.norm(xk),np.linalg.norm(rk)))

if np.linalg.norm(rk) <1.0e-16:

print(“A good approximation solution is obtained”)

return xk

Adk = np.matmul(A,dk)

alphak = np.vdot(rk,rk)/np.vdot(dk,Adk)

xkp = xk + alphak*dk

res = xkp-xk

if np.linalg.norm(res) < tol:

print(“A good approximation solution is obtained”)

return xk

xk = xkp

一、Python所有方向的学习路线

Python所有方向的技术点做的整理，形成各个领域的知识点汇总，它的用处就在于，你可以按照下面的知识点去找对应的学习资源，保证自己学得较为全面。

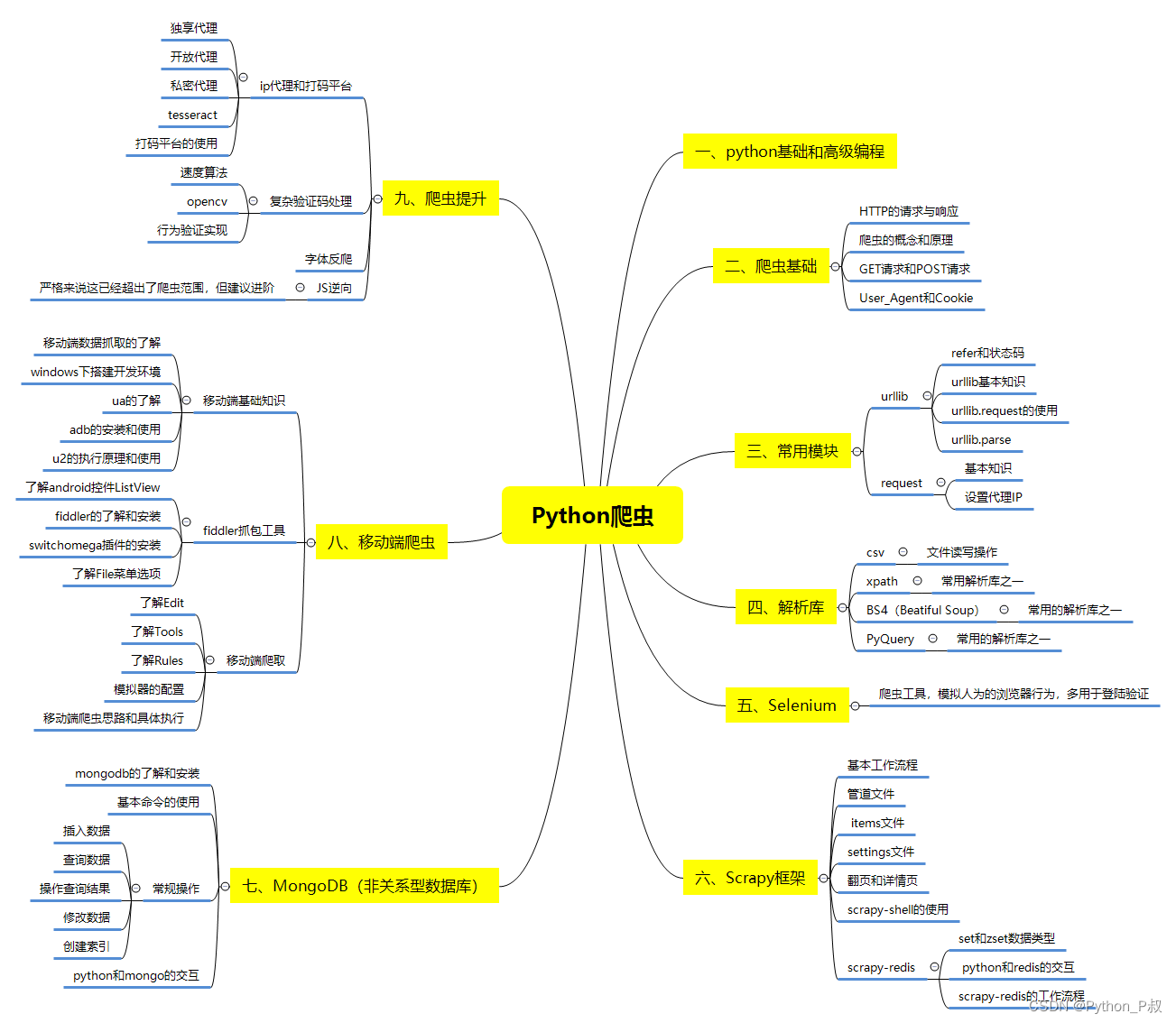
二、Python必备开发工具

工具都帮大家整理好了，安装就可直接上手！

三、最新Python学习笔记

当我学到一定基础，有自己的理解能力的时候，会去阅读一些前辈整理的书籍或者手写的笔记资料，这些笔记详细记载了他们对一些技术点的理解，这些理解是比较独到，可以学到不一样的思路。

四、Python视频合集

观看全面零基础学习视频，看视频学习是最快捷也是最有效果的方式，跟着视频中老师的思路，从基础到深入，还是很容易入门的。

五、实战案例

纸上得来终觉浅，要学会跟着视频一起敲，要动手实操，才能将自己的所学运用到实际当中去，这时候可以搞点实战案例来学习。

六、面试宝典

简历模板

网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。

需要这份系统化学习资料的朋友，可以戳这里无偿获取

一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！