目录
一、支持向量机简介
支持向量机(Support Vector Machines, SVM)是一种监督学习模型,用于解决二分类问题,在机器学习领域有着广泛的应用。SVM通过在样本空间中寻找一个划分超平面,将不同类别的样本分开,同时使得两个点集到此平面的距离(即间隔)最大,因此又被称为最大间隔超平面。
1.1、硬间隔
硬间隔SVM试图找到一个能够完全分离数据的超平面。这适用于线性可分的数据集,但在实际应用中,数据往往是线性不可分的,这使得硬间隔SVM在实践中不太常用。硬间隔SVM的目标是最大化超平面的间隔(即离决策边界最近的样本到超平面的最小距离),同时保证所有样本都被正确分类。
具体地,硬间隔SVM的问题可以表述为:
其中:
- (
) 是超平面的法向量
- (b) 是超平面的偏置项
- (y_i) 是第 (i) 个样本的标签(+1 或 -1)
- (
) 是第 (i) 个样本的特征向量
1.2、软间隔
软间隔SVM通过引入松弛变量来允许一定程度的分类错误,从而更适用于现实中的线性不可分数据。软间隔SVM在寻找超平面的过程中,不仅要最大化间隔,还要平衡分类错误的数量。
具体地,软间隔SVM的问题可以表述为:
其中:
- (
) 是松弛变量,表示第 (i) 个样本允许的误差
- (C) 是惩罚参数,控制间隔最大化和分类错误之间的权衡。较大的 (C) 值会减少分类错误但可能导致过拟合;较小的 (C) 值会增加分类错误但可能提升模型的泛化能力
1.3拉格朗日乘数法
支持向量机(SVM)的优化问题通常使用拉格朗日乘数法进行求解。拉格朗日方法帮助我们将原始的优化问题转化为对偶问题,从而更容易求解。下面详细介绍硬间隔SVM和软间隔SVM的拉格朗日形式。
硬间隔SVM的拉格朗日形式
硬间隔SVM的目标是找到最大化间隔的超平面,同时保证所有样本都被正确分类。其优化问题为:
为了将其转化为拉格朗日形式,我们引入拉格朗日乘数 ,对应于每个约束条件
。拉格朗日函数定义为:
为了找到最优解,我们需要对 和 (b) 求偏导并令其等于零:
将这些条件代入拉格朗日函数,得到对偶问题:
软间隔SVM的拉格朗日形式
软间隔SVM允许分类错误,并引入松弛变量 。其优化问题为:
引入拉格朗日乘数 和
对应于每个约束条件
。拉格朗日函数为:
同样,对 , (b), 和
求偏导并令其等于零:
将这些条件带入拉格朗日函数中,得到软间隔SVM的对偶问题:
在实际应用中,我们通常通过数值优化方法(如SMO算法)来求解这个对偶问题,从而找到支持向量和决策边界。
1.4、核函数
核函数在支持向量机(SVM)中扮演着重要的角色,它可以将输入空间中的数据映射到高维特征空间,从而使非线性可分的问题在高维空间中变得线性可分。这样可以通过线性分类器(如硬间隔SVM)来处理非线性分类问题。常见的核函数包括线性核、多项式核、高斯核等。
线性核
线性核是最简单的核函数,它直接在原始输入空间中进行线性分类。线性核的形式为:
多项式核
多项式核引入了多项式的非线性映射,可以处理一定程度上的非线性分类问题。多项式核的形式为:
其中,是尺度因子,(r) 是常数项,(d) 是多项式的次数。
二、实例
我的代码是利用支持向量机实现鸢尾花的二分类
2.1、数据处理
利用库中的鸢尾花数据,对鸢尾花中的数据分为训练集与测试集并进行标准化处理
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data # 特征数据
y = iris.target # 标签数据
# 只取两类数据进行二分类
X = X[y != 2] # 去掉第三类
y = y[y != 2] # 去掉第三类的标签
y = np.where(y == 0, -1, 1) # 将类别标签0改为-1
# 数据集划分为训练集和测试集
np.random.seed(42) # 设置随机种子
shuffle_indices = np.random.permutation(len(X)) # 打乱数据
X, y = X[shuffle_indices], y[shuffle_indices] # 重新排序数据
split_index = int(0.7 * len(X)) # 计算70%数据的索引
X_train, X_test = X[:split_index], X[split_index:] # 分割为训练集
y_train, y_test = y[:split_index], y[split_index:] # 分割为测试集
# 标准化特征
mean = X_train.mean(axis=0) # 计算训练集均值
std = X_train.std(axis=0) # 计算训练集标准差
X_train = (X_train - mean) / std # 标准化训练集
X_test = (X_test - mean) / std # 标准化测试集2.2、梯度下降法训练模型
首先初始化权重w和偏置b,然后进行迭代更新。在每次迭代中,遍历训练数据集,检查是否满足条件,如果满足条件,则更新权重;否则,同时更新权重和偏置。
# SVM参数
learning_rate = 0.001 # 学习率
lambda_param = 0.01 # 正则化参数
C = 1.0 # 惩罚参数
num_iterations = 1000 # 迭代次数
# 初始化权重和偏置
w = np.zeros(X_train.shape[1]) # 初始化权重为零
b = 0 # 初始化偏置为零
# 梯度下降法训练模型
for i in range(num_iterations): # 迭代500次
for idx, x_i in enumerate(X_train):
condition = y_train[idx] * (np.dot(x_i, w) + b) >= 1 # 检查是否满足条件
if condition:
w -= learning_rate * (2 * lambda_param * w) # 更新权重
else:
w -= learning_rate * (2 * lambda_param * w - np.dot(x_i, y_train[idx]) * C) # 更新权重
b -= learning_rate * y_train[idx] * C # 更新偏置
2.3、预测正确率
def predict(X):
return np.sign(np.dot(X, w) + b) # 计算预测值
# 测试模型
y_pred = predict(X_test) # 预测测试集
# 计算准确率
accuracy = np.mean(y_pred == y_test) # 计算准确率
print(f'Accuracy: {accuracy:.2f}')
2.4、显示正负类结果
函数接受两个参数:y_true表示真实标签,y_pred表示预测标签。函数首先计算真正例(TP)、真负例(TN)、假正例(FP)和假负例(FN),然后分别计算正类和负类的精确度、召回率和F1分数,并将结果打印出来。
def classification_report(y_true, y_pred):
tp = np.sum((y_true == 1) & (y_pred == 1)) # 真正例
tn = np.sum((y_true == -1) & (y_pred == -1)) # 真负例
fp = np.sum((y_true == -1) & (y_pred == 1)) # 假正例
fn = np.sum((y_true == 1) & (y_pred == -1)) # 假负例
precision_pos = tp / (tp + fp) if tp + fp > 0 else 0 # 计算正类精度
recall_pos = tp / (tp + fn) if tp + fn > 0 else 0 # 计算正类召回率
f1_pos = 2 * (precision_pos * recall_pos) / (precision_pos + recall_pos) if precision_pos + recall_pos > 0 else 0 # 计算正类F1
precision_neg = tn / (tn + fn) if tn + fn > 0 else 0 # 计算负类精度
recall_neg = tn / (tn + fp) if tn + fp > 0 else 0 # 计算负类召回率
f1_neg = 2 * (precision_neg * recall_neg) / (precision_neg + recall_neg) if precision_neg + recall_neg > 0 else 0 # 计算负类F1
print(f"Class -1: Precision: {precision_neg:.2f}, Recall: {recall_neg:.2f}, F1-score: {f1_neg:.2f}") # 打印负类报告
print(f"Class 1: Precision: {precision_pos:.2f}, Recall: {recall_pos:.2f}, F1-score: {f1_pos:.2f}") # 打印正类报告2.5、绘图
def plot_decision_boundary(X, y, w, b):
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 # 设置x轴范围
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 # 设置y轴范围
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02), np.arange(x2_min, x2_max, 0.02)) # 创建网格
grid = np.c_[xx1.ravel(), xx2.ravel()] # 网格点
Z = predict_2d((grid - mean_2d) / std_2d) # 使用前两个特征的均值和标准差进行标准化
Z = Z.reshape(xx1.shape) # 预测值形状调整
plt.contourf(xx1, xx2, Z, colors=['lightgray', 'lightyellow'], alpha=0.3) # 绘制等高线
# 绘制支持向量
distance_from_hyperplane = np.abs(np.dot(X, w) + b - 1) # 距离超平面距离
sv = distance_from_hyperplane < 0.1 # 找到支持向量
plt.scatter(X[sv, 0], X[sv, 1], s=200, facecolors='none', edgecolors='k') # 绘制支持向量
# 绘制所有样本
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k') # 绘制样本点
plt.xlabel('Feature 1') # x轴标签
plt.ylabel('Feature 2') # y轴标签
plt.title('SVM Decision Boundary and Support Vectors') # 图标题
plt.show()
三、实验中遇到的问题
在实验过程中改变了训练模型的训练次数后,他的超平面会发生很大的改变,这是迭代次数为1000次时的图像:
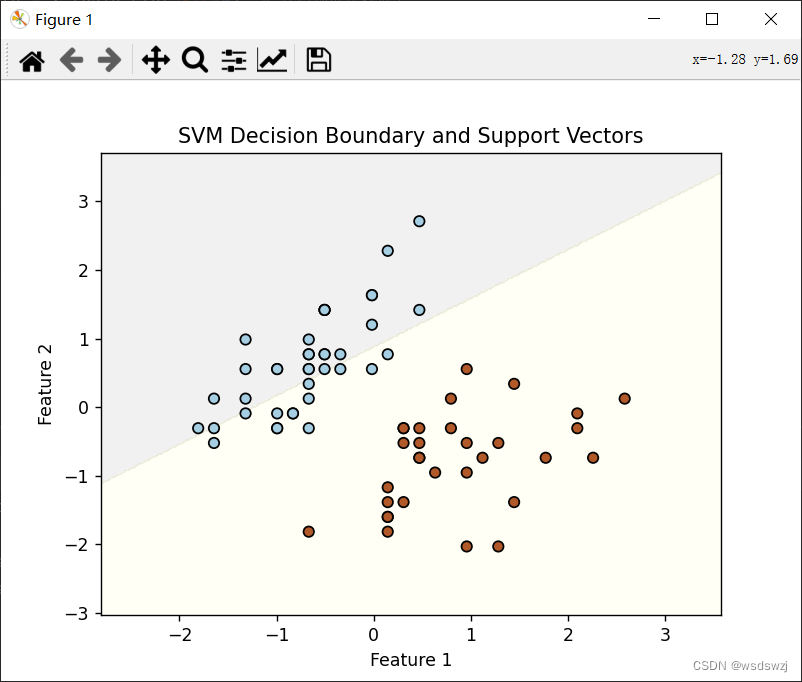
而这是迭代次数为500次的图像:

四、总结
优点
-
有效处理高维数据:SVM在高维空间中表现优异,能够处理特征维数大于样本数的情况。它的性能不会因为特征数量多而显著下降。
-
支持非线性分类:通过核函数,SVM可以将原始数据映射到高维空间,从而能够有效地处理非线性分类问题。常用的核函数如线性核、多项式核、高斯核等。
-
健壮性强:SVM对少量的噪声和异常值具有一定的鲁棒性,尤其是软间隔SVM,它通过引入松弛变量来允许一定程度的误分类。
-
理论基础扎实:SVM基于统计学习理论中的结构风险最小化原则,其目标是找到一个能够最大化分类间隔的超平面,从而在理论上能保证较好的泛化能力。
-
唯一解:由于SVM的优化问题是一个凸优化问题,其解是全局最优且唯一的,这避免了像神经网络那样可能陷入局部最优的问题。
缺点
-
计算复杂度高:对于大规模数据集,SVM的训练时间和内存需求会急剧增加,特别是在使用非线性核函数时。这使得SVM在处理大规模数据时效率不高。
-
参数选择复杂:SVM模型有多个超参数(如惩罚参数 (C) 和核函数参数 (\sigma) 等),这些参数的选择对模型性能影响很大,通常需要通过交叉验证等方法进行调优。
-
对缺失数据敏感:SVM对缺失数据较为敏感,需要在训练前对数据进行预处理,确保数据完整性。
-
解释性差:与决策树等模型相比,SVM模型的可解释性较差,难以提供直观的规则或逻辑来解释分类结果。
-
不能直接输出概率:SVM本质上是一个二分类器,虽然可以通过一些后处理方法(如Platt缩放)来输出分类概率,但这些方法增加了额外的复杂度。
五、代码
、
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets
# 加载鸢尾花数据集
iris = datasets.load_iris()
X = iris.data # 特征数据
y = iris.target # 标签数据
# 只取两类数据进行二分类
X = X[y != 2] # 去掉第三类
y = y[y != 2] # 去掉第三类的标签
y = np.where(y == 0, -1, 1) # 将类别标签0改为-1
# 数据集划分为训练集和测试集
np.random.seed(42) # 设置随机种子
shuffle_indices = np.random.permutation(len(X)) # 打乱数据
X, y = X[shuffle_indices], y[shuffle_indices] # 重新排序数据
split_index = int(0.7 * len(X)) # 计算70%数据的索引
X_train, X_test = X[:split_index], X[split_index:] # 分割为训练集
y_train, y_test = y[:split_index], y[split_index:] # 分割为测试集
# 标准化特征
mean = X_train.mean(axis=0) # 计算训练集均值
std = X_train.std(axis=0) # 计算训练集标准差
X_train = (X_train - mean) / std # 标准化训练集
X_test = (X_test - mean) / std # 标准化测试集
# SVM参数
learning_rate = 0.001 # 学习率
lambda_param = 0.01 # 正则化参数
C = 1.0 # 惩罚参数
num_iterations = 500 # 迭代次数
# 初始化权重和偏置
w = np.zeros(X_train.shape[1]) # 初始化权重为零
b = 0 # 初始化偏置为零
# 梯度下降法训练模型
for i in range(num_iterations): # 迭代500次
for idx, x_i in enumerate(X_train):
condition = y_train[idx] * (np.dot(x_i, w) + b) >= 1 # 检查是否满足条件
if condition:
w -= learning_rate * (2 * lambda_param * w) # 更新权重
else:
w -= learning_rate * (2 * lambda_param * w - np.dot(x_i, y_train[idx]) * C) # 更新权重
b -= learning_rate * y_train[idx] * C # 更新偏置
# 预测函数
def predict(X):
return np.sign(np.dot(X, w) + b) # 计算预测值
# 测试模型
y_pred = predict(X_test) # 预测测试集
# 计算准确率
accuracy = np.mean(y_pred == y_test) # 计算准确率
print(f'Accuracy: {accuracy:.2f}')
# 打印分类报告
def classification_report(y_true, y_pred):
tp = np.sum((y_true == 1) & (y_pred == 1)) # 真正例
tn = np.sum((y_true == -1) & (y_pred == -1)) # 真负例
fp = np.sum((y_true == -1) & (y_pred == 1)) # 假正例
fn = np.sum((y_true == 1) & (y_pred == -1)) # 假负例
precision_pos = tp / (tp + fp) if tp + fp > 0 else 0 # 计算正类精度
recall_pos = tp / (tp + fn) if tp + fn > 0 else 0 # 计算正类召回率
f1_pos = 2 * (precision_pos * recall_pos) / (precision_pos + recall_pos) if precision_pos + recall_pos > 0 else 0 # 计算正类F1
precision_neg = tn / (tn + fn) if tn + fn > 0 else 0 # 计算负类精度
recall_neg = tn / (tn + fp) if tn + fp > 0 else 0 # 计算负类召回率
f1_neg = 2 * (precision_neg * recall_neg) / (precision_neg + recall_neg) if precision_neg + recall_neg > 0 else 0 # 计算负类F1
print(f"Class -1: Precision: {precision_neg:.2f}, Recall: {recall_neg:.2f}, F1-score: {f1_neg:.2f}") # 打印负类报告
print(f"Class 1: Precision: {precision_pos:.2f}, Recall: {recall_pos:.2f}, F1-score: {f1_pos:.2f}") # 打印正类报告
classification_report(y_test, y_pred)
# 打印混淆矩阵
def confusion_matrix(y_true, y_pred):
tp = np.sum((y_true == 1) & (y_pred == 1)) # 真正例
tn = np.sum((y_true == -1) & (y_pred == -1)) # 真负例
fp = np.sum((y_true == -1) & (y_pred == 1)) # 假正例
fn = np.sum((y_true == 1) & (y_pred == -1)) # 假负例
return np.array([[tn, fp],
[fn, tp]]) # 返回混淆矩阵
print('Confusion Matrix:')
print(confusion_matrix(y_test, y_pred))
# 使用前两个特征进行绘制
X_train_2d = X_train[:, :2] # 取前两个特征
w_2d = w[:2] # 取前两个特征的权重
# 标准化前两个特征的均值和标准差
mean_2d = mean[:2] # 前两个特征的均值
std_2d = std[:2] # 前两个特征的标准差
# 定义用于预测的函数
def predict_2d(X):
return np.sign(np.dot(X, w_2d) + b) # 计算二维特征的预测值
# 绘制决策边界和支持向量
def plot_decision_boundary(X, y, w, b):
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1 # 设置x轴范围
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1 # 设置y轴范围
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.02), np.arange(x2_min, x2_max, 0.02)) # 创建网格
grid = np.c_[xx1.ravel(), xx2.ravel()] # 网格点
Z = predict_2d((grid - mean_2d) / std_2d) # 使用前两个特征的均值和标准差进行标准化
Z = Z.reshape(xx1.shape) # 预测值形状调整
plt.contourf(xx1, xx2, Z, colors=['lightgray', 'lightyellow'], alpha=0.3) # 绘制等高线
# 绘制支持向量
distance_from_hyperplane = np.abs(np.dot(X, w) + b - 1) # 距离超平面距离
sv = distance_from_hyperplane < 0.1 # 找到支持向量
plt.scatter(X[sv, 0], X[sv, 1], s=200, facecolors='none', edgecolors='k') # 绘制支持向量
# 绘制所有样本
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Paired, edgecolors='k') # 绘制样本点
plt.xlabel('Feature 1') # x轴标签
plt.ylabel('Feature 2') # y轴标签
plt.title('SVM Decision Boundary and Support Vectors') # 图标题
plt.show()
# 使用前两个特征调用绘制函数
plot_decision_boundary(X_train_2d, y_train, w_2d, b)
结果























 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








