周博磊 第6章 优化策略的进阶
回顾
Value-based RL vs Policy-based RL
- 基于价值的强化学习是一种隐事的确定性策略,最大化Q函数得到
- 基于策略的强化学习是随机性策略,由策略函数所决定
AC 减少方差的方式
A π = Q π ( s , a ) − V π A^{\pi} = Q^{\pi}(s, a) - V^{\pi} Aπ=Qπ(s,a)−Vπ
梯度:
∇
J
(
θ
)
=
E
π
θ
[
∇
θ
log
π
θ
(
s
,
a
)
A
π
θ
(
s
,
a
)
]
\nabla J(\theta) = \mathbb{E}_{\pi_{\theta}}[\nabla_{\theta} \log\pi_{\theta}(s, a) A^{\pi_{\theta}}(s, a) ]
∇J(θ)=Eπθ[∇θlogπθ(s,a)Aπθ(s,a)]
不同时间维度上的Critic
MC:
∇
κ
=
α
(
G
t
−
V
κ
(
s
)
)
ψ
(
s
)
\nabla \kappa = \alpha (G_{t} - V_{\kappa}(s)) \psi(s)
∇κ=α(Gt−Vκ(s))ψ(s)
TD(0)
∇
κ
=
α
(
r
+
γ
V
ψ
(
s
′
)
−
V
κ
(
s
)
)
ψ
(
s
)
\nabla \kappa = \alpha (r + \gamma V_{\psi}(s^{'}) - V_{\kappa}(s)) \psi(s)
∇κ=α(r+γVψ(s′)−Vκ(s))ψ(s)
k-step
∇
κ
=
α
(
∑
i
=
0
k
γ
i
r
t
+
i
+
γ
k
V
κ
(
s
t
+
k
)
−
V
κ
(
s
)
)
ψ
(
s
)
\nabla \kappa = \alpha (\sum_{i=0}^{k}\gamma^{i}r_{t+i} + \gamma^{k}V_{\kappa}(s_{t+k}) - V_{\kappa}(s)) \psi(s)
∇κ=α(i=0∑kγirt+i+γkVκ(st+k)−Vκ(s))ψ(s)
不同时间维度上的Actors
MC:
∇
κ
=
α
(
G
t
−
V
κ
(
s
)
)
∇
θ
log
π
θ
(
s
t
,
a
t
)
\nabla \kappa = \alpha (G_{t} - V_{\kappa}(s)) \nabla_{\theta}\log\pi_{\theta}(s_{t}, a_{t})
∇κ=α(Gt−Vκ(s))∇θlogπθ(st,at)
TD(0)
∇
κ
=
α
(
r
+
γ
V
ψ
(
s
′
)
−
V
κ
(
s
)
)
∇
θ
log
π
θ
(
s
t
,
a
t
)
\nabla \kappa = \alpha (r + \gamma V_{\psi}(s^{'}) - V_{\kappa}(s)) \nabla_{\theta}\log\pi_{\theta}(s_{t}, a_{t})
∇κ=α(r+γVψ(s′)−Vκ(s))∇θlogπθ(st,at)
k-step
∇
κ
=
α
(
∑
i
=
0
k
γ
i
r
t
+
i
+
γ
k
V
κ
(
s
t
+
k
)
−
V
κ
(
s
)
)
∇
θ
log
π
θ
(
s
t
,
a
t
)
\nabla \kappa = \alpha (\sum_{i=0}^{k}\gamma^{i}r_{t+i} + \gamma^{k}V_{\kappa}(s_{t+k}) - V_{\kappa}(s)) \nabla_{\theta}\log\pi_{\theta}(s_{t}, a_{t})
∇κ=α(i=0∑kγirt+i+γkVκ(st+k)−Vκ(s))∇θlogπθ(st,at)
State of Art
Policy-Based
TRPO -> ACKER -> PPO
Value-Based
DDPG->TD3->SAC
Policy Gradient 缺点
- 数据采样效率较低
- 不合适的步长会导致训练崩掉
step too far -> bad policy -> bad data collection
Natural Policy Gradient
Policy Gradient:
d
∗
=
∇
θ
J
(
θ
)
=
lim
ϵ
⇒
0
1
ϵ
max
J
(
θ
+
d
)
,
s
t
.
∣
∣
d
∣
∣
<
=
ϵ
d^{*} = \nabla_{\theta}J(\theta) = \lim_{\epsilon \Rightarrow 0} \frac{1}{\epsilon} \max J(\theta + d), st. ||d|| <= \epsilon
d∗=∇θJ(θ)=ϵ⇒0limϵ1maxJ(θ+d),st.∣∣d∣∣<=ϵ
缺点
对于policy 的函数形式过于敏感,不同的softmax,gaussian都会导致不同的优化结果
在分布空间最大的提升
d
∗
=
arg max
J
(
θ
+
d
)
,
s
.
t
.
K
L
(
π
θ
∣
∣
π
π
+
d
)
=
c
d^{*} = \argmax J(\theta + d), s.t. KL(\pi_{\theta} || \pi_{\pi + d}) = c
d∗=argmaxJ(θ+d),s.t.KL(πθ∣∣ππ+d)=c
固定KL在一个常数c内,可以保证我们的分布以常数的速度进行优化。不用考虑模型函数的参数构造方式。
- KL 散度是衡量两个分布的距离
K L ( p ∣ ∣ q ) = ∑ i = 1 n p i log p i q i KL(p||q) = \sum_{i=1}^{n}p_{i} \log \frac{p_{i}}{q_{i}} KL(p∣∣q)=∑i=1npilogqipi
K L ( p ∣ ∣ q ) ) = E ( log p i − log q i ) KL(p||q)) = \mathbb{E}(\log p_{i} - \log q_{i}) KL(p∣∣q))=E(logpi−logqi) - 虽然KL 散度是非对称的,但是d趋近于0时。KL散度可以认为是对称的。所以在局部内,我们可以认为KL散度是对称矩阵。
- 我们可以证明KL 散度的二阶泰勒展开式:
K L ( π θ ∣ ∣ π θ + d ) ≈ 1 2 d T F d KL(\pi_{\theta} || \pi_{\theta + d}) \approx \frac{1}{2} d^{T} F d KL(πθ∣∣πθ+d)≈21dTFd
F 是Fisher Information Matrix, 是KL散度的二阶导数 E π θ [ ∇ log π θ ∇ log π θ T ] \mathbb{E_{\pi_{\theta}}} [\nabla \log \pi_{\theta} \nabla \log \pi_{\theta} ^{T}] Eπθ[∇logπθ∇logπθT]
流程:
d
∗
=
arg max
J
(
θ
+
d
)
,
s
.
t
.
K
L
(
π
θ
∣
∣
π
π
+
d
)
=
c
d^{*} = \argmax J(\theta + d), s.t. KL(\pi_{\theta} || \pi_{\pi + d}) = c
d∗=argmaxJ(θ+d),s.t.KL(πθ∣∣ππ+d)=c
上述可以写成拉格朗日形式,
J
(
θ
+
d
)
J(\theta + d)
J(θ+d)写成一阶泰勒展开,受限的KL散度可以写成二阶泰勒展开
d
∗
=
arg max
d
J
(
θ
+
d
)
−
λ
(
K
L
(
π
π
∣
∣
π
θ
+
d
)
−
c
)
≈
arg max
d
J
(
θ
)
+
∇
θ
J
(
θ
)
T
d
−
1
2
λ
d
T
F
d
+
λ
c
d^{*} = \argmax_{d} J(\theta + d) - \lambda (KL(\pi_{\pi} || \pi_{\theta + d}) - c) \\ \approx \argmax_{d} J(\theta) + \nabla_{\theta}J(\theta)^{T}d - \frac{1}{2} \lambda d^{T}Fd + \lambda c
d∗=dargmaxJ(θ+d)−λ(KL(ππ∣∣πθ+d)−c)≈dargmaxJ(θ)+∇θJ(θ)Td−21λdTFd+λc
令d = 0, natural policy 梯度:
d
=
1
λ
F
−
1
∇
θ
J
(
θ
)
d = \frac{1}{\lambda} F^{-1} \nabla_{\theta}J(\theta)
d=λ1F−1∇θJ(θ)
-
Natural Policy Graident 是二阶导优化,与模型参数化形式无关。
θ t + 1 = θ t + α F − 1 ∇ θ J ( θ ) \theta_{t+1} = \theta_{t} + \alpha F^{-1} \nabla_{\theta}J(\theta) θt+1=θt+αF−1∇θJ(θ)
F = E π θ [ ∇ log π θ ∇ log π θ T ] F = \mathbb{E_{\pi_{\theta}}} [\nabla \log \pi_{\theta} \nabla \log \pi_{\theta} ^{T}] F=Eπθ[∇logπθ∇logπθT],是fisher information matrix 也是KL散度的二阶导数 -
Natural Policy 无关于模型的方式
-
详细推导 https://wiseodd.github.io/techblog/2018/03/14/natural-gradient/
重要性采样
x是基于p分布采样得到的数据,我们可以通过q分布采样得到数据,使用p q间的概率比值来重新娇艳结果
E
x
∈
p
[
f
(
x
)
]
=
∫
q
(
x
)
p
(
x
)
q
(
x
)
f
(
x
)
d
x
=
E
x
∈
q
[
p
(
x
)
q
(
x
)
f
(
x
)
]
\mathbb{E}_{x \in p} [f(x)] = \int q(x)\frac{p(x)}{q(x)} f(x)dx = \mathbb{E}_{x \in q} [\frac{p(x)}{q(x)}f(x)]
Ex∈p[f(x)]=∫q(x)q(x)p(x)f(x)dx=Ex∈q[q(x)p(x)f(x)]
NPG算法流程:

TRPO算法流程:

详细的算法说明:
ACKTR(Actor-Critic using Kronecker-Factored Trust Region)
使用Kronecker-factored approximation(K-FAC)减少计算Fisher Information Matrix 逆的复杂度
ACKTR
PPO(Proximal Policy Optimization) 近端策略优化
算法流程:
带有KL散度惩罚的流程:

with Clipping
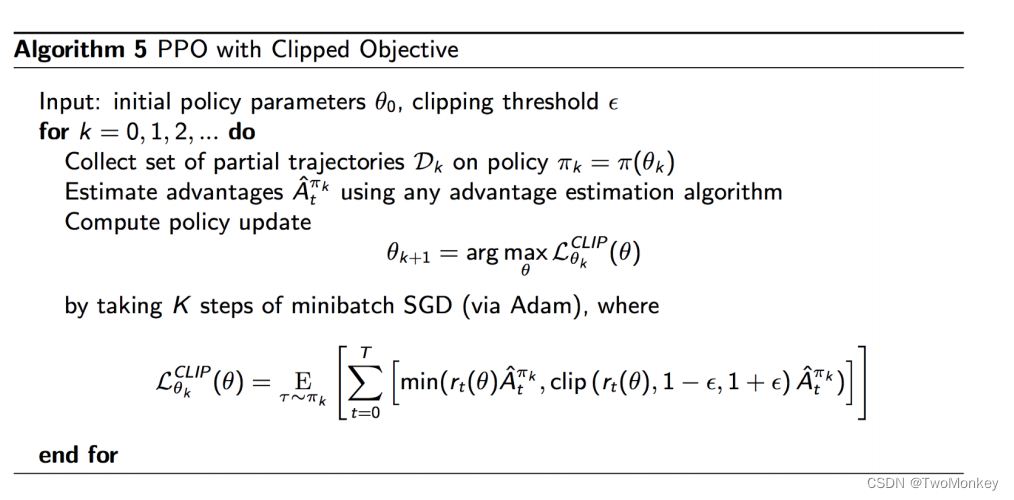
tips:
对atari 不熟的话,可以试玩
Atari 试玩
DDPG
Q-target:
y
(
r
,
s
′
,
d
)
=
r
+
γ
(
1
−
d
)
Q
(
s
′
,
μ
t
a
r
g
e
t
(
s
′
)
)
y(r, s^{'}, d) = r + \gamma (1 - d) Q(s^{'}, \mu_{target}(s^{'}))
y(r,s′,d)=r+γ(1−d)Q(s′,μtarget(s′))
Q-function:
min
E
s
,
r
,
s
′
,
d
∈
D
[
Q
ϕ
(
s
,
a
)
−
y
(
r
,
s
′
,
d
)
]
\min \mathbb{E}_{s, r, s^{'}, d \in D} [Q_{\phi}(s, a) - y(r, s^{'}, d)]
minEs,r,s′,d∈D[Qϕ(s,a)−y(r,s′,d)]
policy:
max
θ
E
s
∈
D
[
Q
ϕ
(
s
,
μ
θ
(
s
)
)
]
\max_{\theta} \mathbb{E}_{s \in D}[Q_{\phi}(s, \mu_{\theta}(s))]
maxθEs∈D[Qϕ(s,μθ(s))]
代码 DDPG
TD3(Twin Delayed DDPG)
DDPG缺点
DDPG过高的估计了Q值,导致策略不够稳定
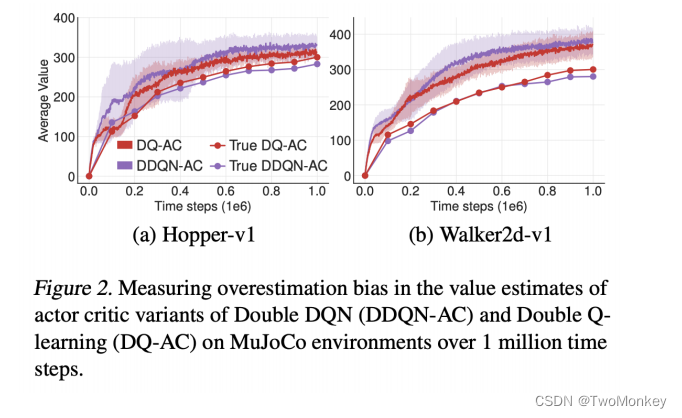
TD3 是在DDPG基础上,添加了一些trick
- Clipped Double-Q Learning
TD3 使用了两个Q函数,用较小的Q值来作为贝尔曼误差的target - Delayed
策略网络的更新速度比q函数更新更慢 - Target Policy Smoothing
TD3在目标函动作上添加了噪声、
TD3 代码
Soft Actor-Critic (SAC)
SAC 是一个离线的训练方法,该方法包含了Entropy regularization的方法
π
∗
=
arg max
E
τ
∼
π
[
∑
t
γ
t
(
R
(
s
t
,
a
t
,
s
t
+
1
)
+
α
H
(
π
(
.
∣
s
t
)
)
)
]
\pi^{*} = \argmax \mathbb{E}_{\tau \sim \pi}[\sum _{t}\gamma^{t}(R(s_{t}, a_{t},s_{t+1}) + \alpha H(\pi(.|s_{t})))]
π∗=argmaxEτ∼π[t∑γt(R(st,at,st+1)+αH(π(.∣st)))]
-
SAC类似于TD3,包含了两个Q 函数
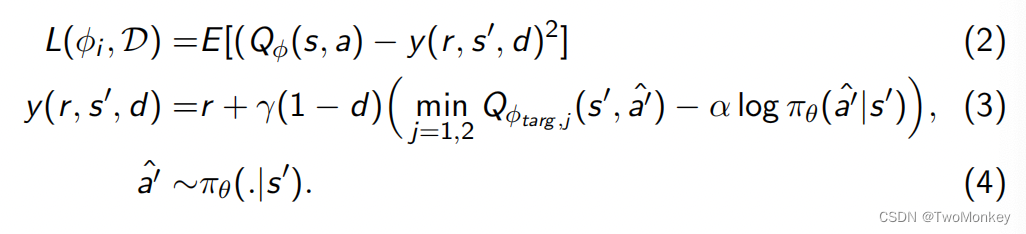
-
Policy 通过最大化Q函数来获得
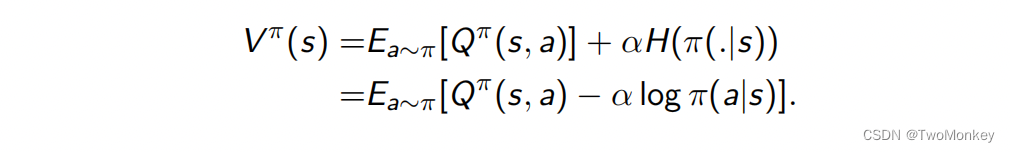
Reparametrize trick
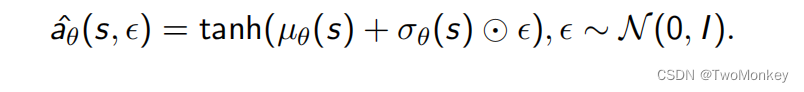
Reparameterization trick允许我们将基于动作分布的期望改成基于随机分布的期望
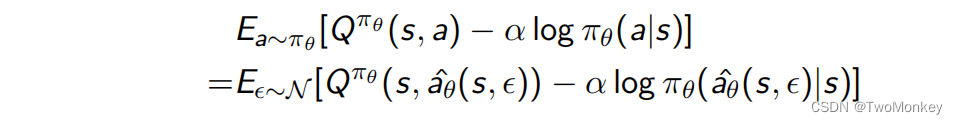























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








