【强化学习】周博磊第2章 马尔科夫决策过程

周博磊 第2章 马尔科夫决策过程

MDP

• Markov Process 马尔科夫过程
• Markov Reward Process 马尔科夫奖励过程
• Markov Decision Proces 马尔科夫决策过程

MDP性质

The furture is independent of the past given the present.
未来的状态只与当前的状态相关

Markov Prcess / Markov Chain

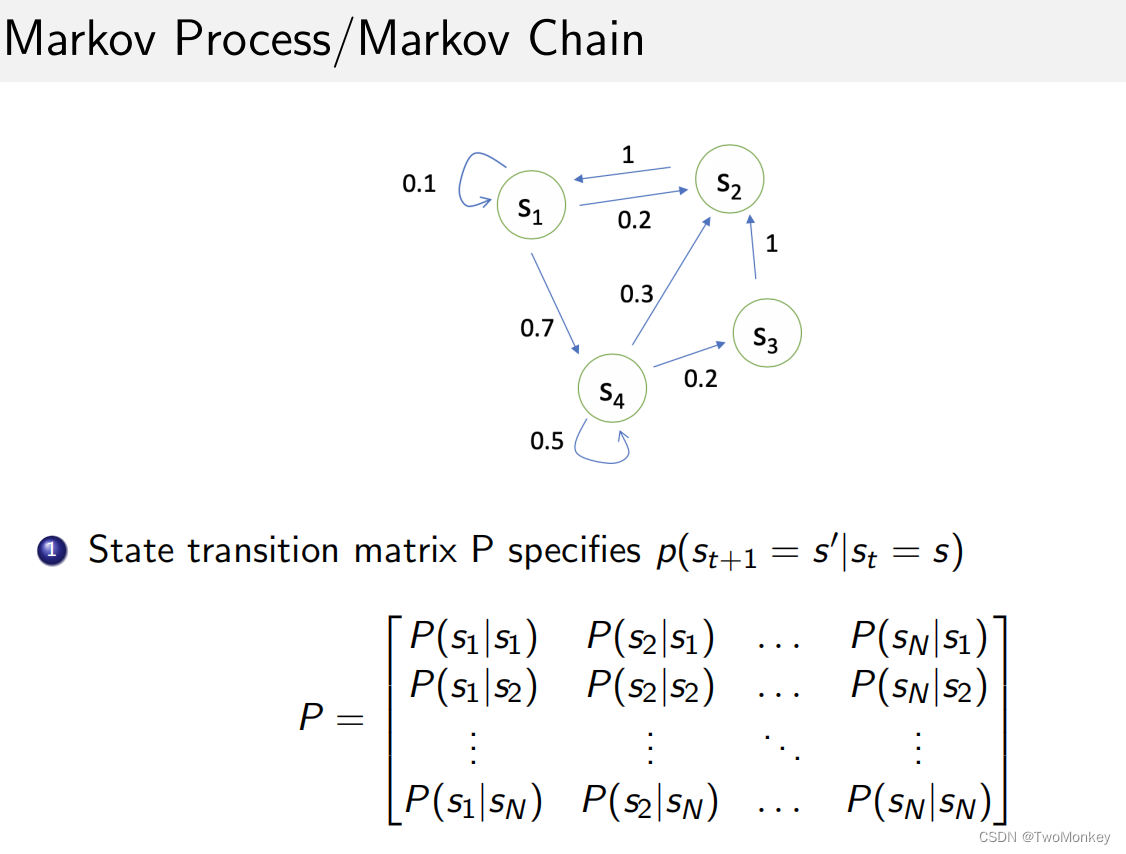
Markov Reward Process

1. S 状态
2. P 动态转移矩阵
3. R 奖励函数 $R(s_t=s)=\mathbb{E}[r_t|S_t=s]$
4. $\gamma$ 折扣因子

Return && Vaule Function

1. Horizon：每个Episode的最大步长
2. Return： Horizon的折扣奖励
   $$G_t=R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{T-t-1}{R}_T$$
3. $V_t(s)$ : Return的期望
   $$\begin{gathered} V_t=\mathbb{E}[G_t|s_t=s] \\ =\mathbb{E}[R_{t+1}+\gamma R_{t+2}+{\gamma }^2{R}_{t+3}+...+{\gamma }^{T-t-1}{R}_T|s_t=s] \end{gathered}$$

折扣因子$\gamma$

• 避免环状的马尔科夫过程
• 未来具有不确定性
• 更加关注即时的奖励

贝尔曼方程

贝尔曼等式描述了状态间的迭代关系
$$V(s)=R(s)+\gamma \sum _{s^{{}^{\prime }}\in S}P(s^{{}^{\prime }}|s)V(s^{{}^{\prime }})$$

迭代的方式计算MRP

• Dynamic Programming
  

• Monte-Carto evalutation
  

• Temporal-Difference Learning

MDP

马尔科夫决策过程相比与奖励过程，加入了动作。也就是说，未来的状态由当前状态和动作共同决定的。
Markov 链/ MRP: 像随波漂流的小船
Markov 决策过程：可以采取导航行为的小船

1. S 状态
2. A 动作
3. P 动态转移矩阵 $P(s_{t+1}=s^{{}^{\prime }}|s_t=s,a_t=a)$
4. R 奖励函数 $R(s_t=s)=\mathbb{E}[r_t|s_t=s,a_t=a]$
5. $\gamma$ 折扣因子

Policy 策略

Policy 是指在某一状态执行某一动作的概率
$$\pi =P(a_t=a|s=s_t)$$
动态转移方程和奖励由当前状态与动作共同决定
$$P^{\pi }=\sum _{a\in A}\pi (a|s)P(s^{\prime }|s,a)$$
$$R^{\pi }=\sum _{a\in A}\pi (a|s)R(s,a)$$

Value Function 价值函数

• $v^{\pi }(s)$ 在s状态下，基于策略$\pi$ 期望的回报
  $$V^{\pi }=\mathbb{E}[G_t|s_t=s]$$
• $q^{\pi }(s,a)$ 在s状态下，采取行动，基于策略$\pi$ 期望的回报
  $$q^{\pi }(s,a)=\mathbb{E}[G_t|s_t=s,a_t=a]$$
• 两者之间的关系
  $$v^{\pi }(s)=\sum _{a\in A}\pi (a|s)q^{\pi }(s,a)$$

贝尔曼期望方程

$$v^{\pi }(s)={\mathbb{E}}_{\pi }[R_{t+1}+\gamma v^{\pi }(s_{t+1})|s_t=s]$$
$$q^{\pi }(s,a)={\mathbb{E}}_{\pi }[R_{t+1}+\gamma q^{\pi }(s_{t+1},A_{t+1})|s_t=s,A_t=a]$$
两者之间的关系

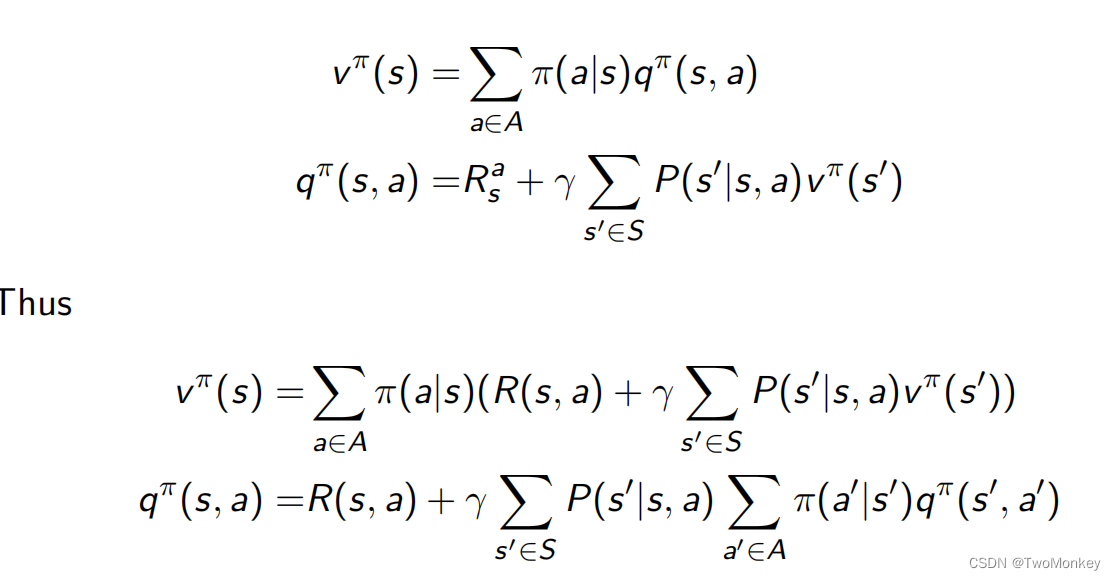
Policy Evalution

已知策略$\pi$ MDP, 计算价值函数$v^{\pi }(s)$
可以用动态规划来做：
$$v_{t+1}(s)=\sum _{a\in A}\pi (a|s)(R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{{}^{\prime }}|s,a)V_t(s^{{}^{\prime }}))$$

Control

已知MDP，寻找最优价值函数和策略
最优函数可以通过寻找最大化$q^{\ast }(s,a)$
$${\pi }^{\ast }(a|s)=\{\begin{array}{lc}1,& ifa=argma{x}_{a\in A}{q}^{\ast }(s,a)\\ 0,& otherwise\end{array}$$

演示样例

动画：
https://cs.stanford.edu/people/karpathy/reinforcejs/gridworld_dp.html
代码：
https://github.com/cuhkrlcourse/RLexample/tree/master/MDP

通过策略迭代更新策略

• 步骤一：基于策略$\pi$计算价值函数
  $$q^{{\pi }_i}(s,a)=R(s,a)+\gamma \sum _{s^{{}^{\prime }}\in S}P(s^{{}^{\prime }}|s,a)v^{{\pi }_i}(s^{\prime })$$
• 步骤二：依据价值函数更新策略
  $${\pi }_{i+1}(s)=\underset{a}{\mathrm{argmax}}{q}^{{\pi }_i(s,a)}$$

值迭代

贝尔曼最优方程

$$\begin{gathered} v^{\ast }=\underset{a}{\max }{q}^{\ast }(s,a) \\ {q}^{\ast }(s,a)=R(s,a)+\gamma \sum _{s^{{}^{\prime }}\in S}P(s^{{}^{\prime }}|s,a)v(s^{{}^{\prime }}) \end{gathered}$$
=>
$$\begin{gathered} v^{\ast }=\underset{a}{\max }R(s,a)+\gamma \sum _{s^{{}^{\prime }}\in S}P(s^{{}^{\prime }}|s,a)v(s^{{}^{\prime }}) \\ {q}^{\ast }(s,a)=R(s,a)+\gamma \sum _{s^{{}^{\prime }}\in S}P(s^{{}^{\prime }}|s,a)\underset{a^{{}^{\prime }}}{\max }{q}^{\ast }(s^{{}^{\prime }},a^{{}^{\prime }}) \end{gathered}$$

策略迭代 VS 价值迭代

• 策略迭代：【策略估计 + 策略更新】作为一个整体过程，需要迭代多次
• 价值阶段：找出最优价值函数 + 策略提取 寻找最优策略是个迭代过程，策略提取取最大价值的动作即是策略。