当图变成了一棵树（纠结的生成树）

最小生成树

经典算法Kruskal算法

int cmp(const node &c,const node &d)
{
    return c.z<d.z;
}

int find(int x)           //路径压缩（没有按秩合并）的并查集
{
    if (fa[x]!=x)
       fa[x]=find(fa[x]);
    return fa[x];
}

int unionn(int f1,int f2)
{
    fa[f1]=f2;
}

int doit()
{
    int i,j=0;
    int tot=0;
    for (i=1;i<=m;i++)
    {
        int r1=find(way[i].u);
        int r2=find(way[i].v);
        if (r1!=r2)
        {
            tot+=way[i].z;
            unionn(r1,r2);
            j++;
        }
        if (j==n-1) break;
    }
    return tot;
}

void Kruskal()
{
    sort(way+1,way+1+m,cmp);
    int size=doit(); 
}

这里不得不提一句什么叫

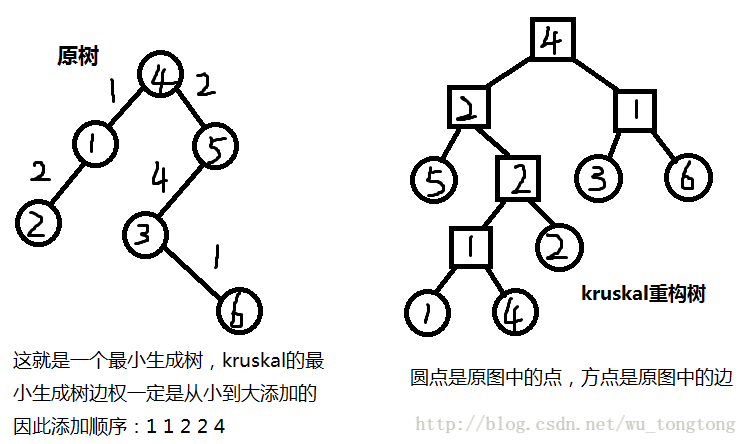
Kruskal重构树

例题
简单的代码讲解

Kruskal重构树可以拿来处理一些最小生成树的边权最值问题
形象的理解就是：
Kruskal连边时并不直接合并两个并查集
而是新建一个节点x
将两个点所在子树都连到x的儿子上

这样生成的树有一些十分优美的性质：

1.二叉树(好吧意义不大)
2.原树与新树两点间路径上边权(点权)的最大值相等
3.子节点的边权小于等于父亲节点(大根堆)
4.原树中两点之间路径上边权的最大值等于新树上两点的LCA的点权

看图理解一下吧

看一下性质的体现：
1.不用说了
2.原树上2—>5:2,新树上也是
3.不用说了
4.1—>6:4
确认满足性质

看一下Kruskal重构树的构建：

维护一个类似并查集的东西

其中有按秩合并和路径压缩
据说这样并查集的时间复杂度才有保证

树的记录方式：爸爸记录法（只记录父亲）
没有必要把树上的边都连起来
结点深度只要调用一个记忆化搜索就好了
（代码还是很丑）

int cmp(const node &a,const node &b)
{
    return a.v<b.v;
}

int find(int a)  //路径压缩 
{
    if (fa[a]!=a) fa[a]=find(fa[a]);
    return fa[a];
}

void kruskal()
{
    sort(e+1,e+1+m,cmp);
    int i,o=0;
    for (int i=1;i<=n;i++) fa[i]=i,size[i]=1;
    for (i=1;i<=m;i++)
    {
        int f1=find(e[i].x);
        int f2=find(e[i].y);
        if (f1!=f2)
        {
            if (size[f1]>size[f2]) swap(f1,f2);  //按秩合并 
            fa[f1]=f2;                           //并查集中的标志节点,f1连到f2上 
            size[f2]=max(size[f2],size[f1]+1);   //size并查集的深度 
            f[f1]=f2;                            //Kruskal重构树中的父节点 
            z[f1]=e[i].v;                        //Kruskal重构树中的结点值（就是原树中的边值） 
        }
    }
}

int getdep(int bh)
{
    if (deep[bh]) return deep[bh];
    if (!f[bh]) return deep[bh]=1;
    return deep[bh]=getdep(f[bh])+1;
}

---

言归正传

为了更好地理解最小生成树，
我们给出两条性质：

性质一：切割性质
假定所有的边权均不相同
设S为既非空集也非全集的V（点集）的子集，
边e是满足一个端点在S内，另一个端点不在S内的所有边中权值最小的边
则图G的所有生成树均包含e

---

性质二：回路性质
假定所有的边权均不同
设C是图G中的任意回路，边e是C上权值最大的边，
则图G的所有生成树不包含e

例1：

每对结点间的最小瓶颈路上的最大边长

解：
求出最小生成树之后：
一般来说，最朴素的用lca（n^2logn）
然而现在有了更好的做法：
用dfs把最小生成树变成有根树，同时计算f(u,v)
当新访问一个结点的时候，考虑所有访问过的老结点，
更新f(x,u)=max(f(x,v),w(u,v))，其中v是u的父结点
复杂度O(n^2)

次小生成树

权值之和排在第二的生成树

最朴素的求法：像次短路一样，次小生成树和最小生成树不会完全一样，
我们枚举最小生成树上的边并删除，在剩下的边里做Kruskal，得到的生成树中权值最小的就是次小生成树
复杂度O(nmα（n,m）)

还有一种更好的方法

枚举要加入哪条新边
在最小生成树上加上一条边u-v，图上会出现一条回路，我们需要删除一条边
所以删除的边一定在最小生成树中u-v的路径上，
由回路性质得，删除的一定是路上的一条最长边
所以我们像例一中一样，求出f(u,v)
剩下的部分只需要O(m)的时间（枚举所有m-n+1条边，O(1)求出新生成树的权值）
时间复杂度O(n^2)

有向最小生成树

给定一个有向带权图G和其中一个结点u，找到一个以u为根结点，权和最小的生成树
有向生成树（directed spanning tree）也叫树形图(arborescence)
是指一个类似树的有向图，满足如下条件

• 恰好有一个入度为0的结点，称为根结点
• 其他结点的入度均为一
• 可以从根节点到达所有其他结点

朱-刘算法

首先是预处理：
删除自环并判断根结点是否可以到达其他结点，如果不是，无解

算法主过程：
首先，给所有非根结点选择一条全最小的入边，
如果选出来的n-1条边构不成圈，则可以证明这些边形成了一个最小树形图
否则把每个圈缩成一个点，继续上述过程

缩圈之后，圈上的所有边都消失了，因此在最终答案的时候需要累加上这些边的权值
但是这样就有一个问题：
假设算法在某次迭代中，把圈C缩成了结点v
则下一次迭代的时候，给v选择的入边将与C中的入弧冲突

如图，圈中已经有了Y—>X，如果收缩之后我们又给X选了一条入边Z—>X
我们就要删除Y—>X（每个非根结点只有一个入度）
这等价于把弧Z—>X减小了Y—>X的权值