受到UVa10288启发之后,我们就可以很容易的求出g[i]表示当前有i张邮票,得到n张得期望步数

同时我们定义pr(x,i)表示买x次能从i种买到n种的概率
实际pr就是这个:
假设我们现在手里已经有了k图案,令s=k/n,拿一个新的图案需要t次的概率:s^(t-1)*(1-s)
则有
设计状态:f[i][j]表示现在有i张不同的邮票,下一次购买需要j+1元,得到n张邮票的期望花费
- i/n的概率,转移到f[i][j+1],花费是j
- (n-i)/n的概率,转移到f[i+1][j+1],花费是j
所以状态转移方程显而易见:
f[i][j]=j + f[i][j+1] * i/n + f[i+1][j+1] * (n-i)/n
但是f[i][j]的j是无限的,所以这个递推无法进行,考虑f[i][j]与f[i][j+1]的关系,有
且有
那么有f[i][j]关于f[i+1][j]的状态转移:
再来看看我们的求解,我们只关心f[0][1]是多少,所以,对于j不等于1的情况我们可以忽略
那么定义F[i]表示f[i][1],有
特别的,f[n][1]=0,所以F[n]=0
我们已知F[n]的值与g[0]~g[n]的值,那么我们就可以递推出f[0][1]=F[0]的值,问题到此就可以解决了
//这里写代码片
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
double g[10010],f[10010];
int n;
int main()
{
scanf("%d",&n);
g[n]=0.0;
for (int i=n-1;i>=0;i--)
g[i]=g[i+1]+(double)n/(n-i);
for (int i=n-1;i>=0;i--)
f[i]=(((f[i+1]+g[i+1])*(double)(n-i)/n)+g[i]*(double)i/n+1.0)*(double)n,f[i]/=(double)n-i;
printf("%.2lf",f[0]);
return 0;
}










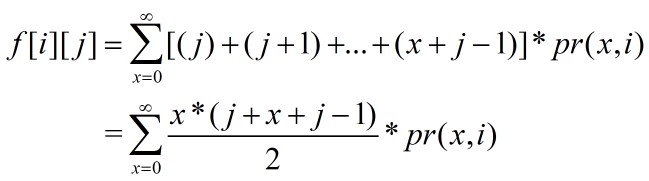
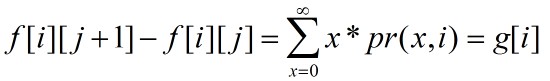
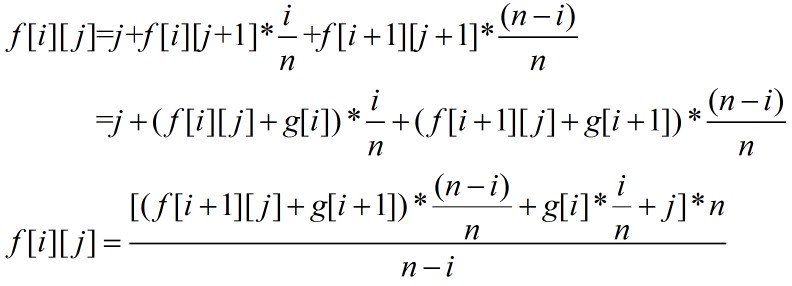
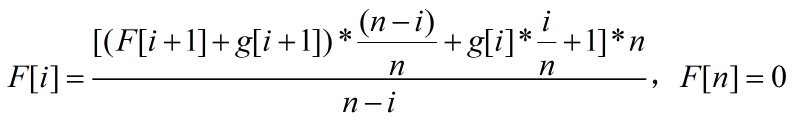














 1422
1422

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








