【网络流】【对偶图】海拔

海拔(noi 2010)

　　YT市是一个规划良好的城市，城市被东西向和南北向的主干道划分为n×n个区域。简单起见，可以将YT市看作一个正方形，每一个区域也可看作一个正方形。从而，YT城市中包括(n+1)×(n+1)个交叉路口和2n×(n+1)条双向道路（简称道路），每条双向道路连接主干道上两个相邻的交叉路口。下图为一张YT市的地图(n = 2)，城市被划分为2×2个区域，包括3×3个交叉路口和12条双向道路。

　　小Z作为该市的市长，他根据统计信息得到了每天上班高峰期间YT市每条道路两个方向的人流量，即在高峰期间沿着该方向通过这条道路的人数。每一个交叉路口都有不同的海拔高度值，YT市市民认为爬坡是一件非常累的事情，每向上爬h的高度，就需要消耗h的体力。如果是下坡的话，则不需要耗费体力。因此如果一段道路的终点海拔减去起点海拔的值为h(注意h可能是负数)，那么一个人经过这段路所消耗的体力是max{0, h}（这里max{a, b}表示取a, b两个值中的较大值）。
　　 小Z还测量得到这个城市西北角的交叉路口海拔为0，东南角的交叉路口海拔为1(如上图所示)，但其它交叉路口的海拔高度都无法得知。小Z想知道在最理想的情况下（即你可以任意假设其他路口的海拔高度），每天上班高峰期间所有人爬坡所消耗的总体力和的最小值。

 

【样例】
样例数据见下图。

最理想情况下所有点的海拔如上图所示。
ans = 3.

【数据规模】
对于20%的数据：n ≤ 3；
对于50%的数据：n ≤ 15；
对于80%的数据：n ≤ 40；
对于100%的数据：1 ≤ n ≤ 500，0 ≤ 流量 ≤ 1,000,000且所有流量均为整数。
【提示】
海拔高度不一定是整数。

上面那句话是一个极没有JJ的人说的，害人。先假设只有0、1两种情况，等一下再来证明。

如果只有0、1，那么要给代价的边必定是01点之间的边，于是就想到了割切，然后要使代价最小，即最小割。

根据定理，我们就来求最大流。左上点和右下点分别在0集和1集中，因此从左上到右下求最大流。

然后来证明只有0、1两种情况。

假设中间点的海拔在0和1之间，则对于左图，把海拔移为1，左边的点的代价会增加，右边的点的代价会减少，总的减少。

对于右图，同理，海拔移为0，总代价也会减少。因此只会有0或1两种情况。

这个方法会超时。。用一种叫对偶图的方法，可以解决。实现方法是将边旋转90°，再加超级源和超级汇。

以下引用Wjj的博文，讲得不错：

朴素算法是从左上角到右下角求一次最大流，求得的这个最大流即为最小割。但这样最多只能得80分（我的程序比较弱，只能过70分）。

于是可以用对偶图优化。
首先可以断定，海拔必为0或1中的一种（不然可以转化为只有0和1的情况），那么可以找到一条0和1的分界线。

我们将平面图上所有的边全都沿中点逆时针旋转90°，将原来每个单位网格的中心点变为对偶图的点，（自然有些边就指向边界外面或是从边界外指向某个点了。）再把对偶图的整个左下区域增加一个超级源，整个右上区域增加一个超级汇，从超级源到超级汇求一次最短路即可。

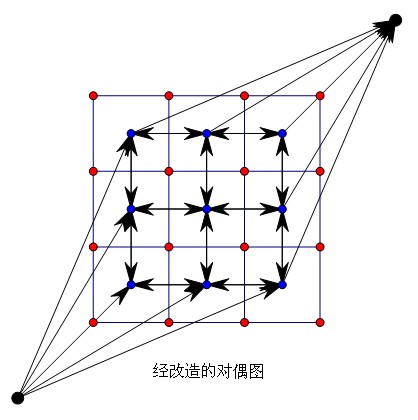
图上很容易看出来，原来的割切必定在现在建的边上，只是意会了，但是不会严格证明。现在从源点到汇点求一次最短路即为原问题的最小割。

现在的代码逐渐整洁起来了，要保持，加油

手大堆。。第一次测看只有两个点超时，其他对了，我还以为手打堆一次性就过了。。。结果错了三个地方：又把SIZE打成n了，忘了判断是否有右儿子，从堆顶取出之后没有标志访问过。改了就过了。

#include <iostream>
#include <queue>
#include <cstdio>
const long maxsum = 251011;
const long maxn = 510;
long n;
long sum;
using std::priority_queue;
typedef long long ll;
const ll inf = 0x7f7f7f7f7f7f7f7fll;
struct node
{
	long ind;
	node *next;
	node *back;
	ll val;	
};
node* head[maxsum];
long _flow1[maxsum];
long _flow2[maxsum];
long _flow3[maxsum];
long _flow4[maxsum];
ll dist[maxsum];
bool vis[maxsum];
struct hnode
{
	long ind;
	ll val;
	bool operator<(const hnode& hn2)const{return val<hn2.val;}	
	hnode(long v,long i):ind(i),val(v){}
	hnode(){}	
};
hnode que[maxsum];
long SIZE = 0;
inline void adjust_up(long l)
{
	while (l>1)
	{
		if (que[l]<que[l>>1]) std::swap(que[l],que[l>>1]);
		else break;	
		l >>= 1;
	}	
}

inline void push(hnode l)
{
	que[++SIZE] = l;
	adjust_up(SIZE);
}

inline void adjust_down(long l)
{
	while ((l<<=1)<SIZE+1)
	{
		if (l<SIZE&&que[l+1]<que[l]) l++;
		if (que[l]<que[l>>1]) std::swap(que[l],que[l>>1]);
		else break;
	}
}

inline void pop()
{
	que[1] = que[SIZE--];
	adjust_down(1);
}

inline void insert(long a,long b,ll c,ll d)
{
	node* n1 = new node;
	n1 -> ind = b;
	n1 -> val = c;
	n1 -> next = head[a];
	head[a] = n1;

	node* n2 = new node;
	n2 -> ind = a;
	n2 -> val = d;
	n2 -> next = head[b];
	head[b] = n2;
	
	n1 -> back = n2;
	n2 -> back = n1;
}

inline void insert(long a,long b,ll c)
{
	node* n1 = new node;
	n1 -> ind = b;
	n1 -> val = c;
	n1 -> next = head[a];
	n1 -> back = 0;
	head[a] = n1;
}

void dijkstra()
{
	for (long i=0;i<sum+2;i++)
	{
		dist[i] = inf;
		vis[i] = false;
	}
	dist[sum] = 0;
	push(hnode(0,sum));
	while (SIZE>0)
	{
		hnode uu = que[1];
		pop();
		long u = uu.ind;
		if (vis[u]) continue;
		vis[u] = true;
		for (node* vv=head[u];vv;vv=vv->next)
		{
			long v = vv->ind;
			if (!vis[v] && dist[v]>dist[u]+vv->val)
			{
				dist[v]=dist[u]+vv->val;
				push(hnode(dist[v],v));
			}
		}	
	}
}

inline int getint()
{
    int res = 0; char tmp;
    while (!isdigit(tmp = getchar()));
    do res = (res << 3) + (res << 1) + tmp - '0';
    while (isdigit(tmp = getchar()));
    return res;
}

int main()
{
	freopen("altitude.in","r",stdin);
	freopen("altitude.out","w",stdout);
	
	n = getint();
	sum = n*n;
	for (long i=0;i<n*(n+1);i++)
	{
		_flow1[i] = getint();
	}
	for (long i=0;i<n*(n+1);i++)
	{
		_flow2[i] = getint();
	}
	for (long i=0;i<n*(n+1);i++)
	{
		_flow3[i] = getint();
	}
	for (long i=0;i<n*(n+1);i++)
	{
		_flow4[i] = getint();	
	}

	for (long i=0;i<n;i++)
	{
		long f = i;
		long t = sum+1;
		insert(f,t,_flow1[i]);	
	}
	for (long i=n*n;i<n*(n+1);i++)
	{
		long f = sum;
		long t = i-n;
		insert(f,t,_flow1[i]);
	}
	
	for (long i=n;i<n*n;i++)
	{
		long f = i;
		long t = i-n;
		insert(f,t,_flow1[i],_flow3[i]);
	}
	
	for (long i=0;i<n*(n+1);i++)
	{
		long x = i/(n+1);
		long y = i%(n+1);
		long f;
		long t;
		
		if (y == 0)
		{
			f = sum;
			t = x*n;
			insert(f,t,_flow2[i]);
		}
		else if (y == n)
		{
			f = (x+1)*n-1;
			t = sum+1;
			insert(f,t,_flow2[i]);
		}
		else
		{
			f = x*n+y-1;
			t = x*n+y;
			insert(f,t,_flow2[i],_flow4[i]);
		}
	}
	dijkstra();
	std::cout << dist[sum+1];
	return 0;	
}

朴素，无对偶图：

#include <cstdio>
#include <iostream>
typedef long long ll;
using std::cout;
const long maxsum = 251011;
const long maxn = 510;
long n = 0;
long sum = 0;

struct node
{
    long ind;
    node *next;
    node *back;
    ll val;    
};
node* head[maxsum];
long D[maxsum];
long DN[maxsum];
#define MIN(a,b) (a<b?a:b)

void insert(long a,long b,ll c,ll d)
{
    node* n1 = new node;
    n1 -> ind = b;
    n1 -> val = c;
    n1 -> next = head[a];
    head[a] = n1;

    node* n2 = new node;
    n2 -> ind = a;
    n2 -> val = d;
    n2 -> next = head[b];
    head[b] = n2;
    
    n1 -> back = n2;
    n2 -> back = n1;
}

long _flow1[maxn*(maxn+1)];
long _flow2[maxn*(maxn+1)];
long _flow3[maxn*(maxn+1)];
long _flow4[maxn*(maxn+1)];

const ll inf = 0x7f7f7f7f7f7f7f7fll;

ll Sap(long u,ll maxflow)
{
    if (u == sum-1)
    {
        return maxflow;
    }
    ll use = 0;
    for (node* vv=head[u];vv;vv=vv->next)
    {
        long v = vv->ind;
        ll tmp ;
        if (vv->val>0 && D[u]==D[v]+1)
        {
            tmp = Sap(v,MIN(maxflow-use,vv->val));
            use += tmp;
            vv->val -= tmp;
            vv->back->val += tmp;
            if (use == maxflow)
                return use;
        }
    }
    if (D[0] >= sum)
        return use;
    if (!(--DN[D[u]]))
        D[0] = sum;
    DN[++D[u]]++;
    return use;    
}

int main()
{
    freopen("altitude.in","r",stdin);
    freopen("altitude.out","w",stdout);
    
    scanf("%ld",&n);
    sum = (n+1)*(n+1);
    for (long i=0;i<n*(n+1);i++)
    {
        scanf("%ld",_flow1+i);
    }
    for (long i=0;i<n*(n+1);i++)
    {
        scanf("%ld",_flow2+i);    
    }
    for (long i=0;i<n*(n+1);i++)
    {
        scanf("%ld",_flow3+i);
    }
    for (long i=0;i<n*(n+1);i++)
    {
        scanf("%ld",_flow4+i);    
    }
    for (long i=0;i<n*(n+1);i++)
    {
        long x = i/n;
        long y = i%n;
        long f = (x*(n+1))+y;
        long t = (x*(n+1))+y+1;
        insert(f,t,_flow1[i],_flow3[i]);
        
        x = i/(n+1);
        y = i%(n+1);
        f = (x*(n+1))+y;
        t = (x*(n+1)+(n+1))+y;
        insert(f,t,_flow2[i],_flow4[i]);
    }
    DN[0] = sum;
    long ans = 0;
    while (D[0] < sum)
    {
        ans += Sap(0,inf);
    }
    cout << ans;
    return 0;
}