8. 吴恩达机器学习课程-作业8-异常检测和推荐系统

fork了别人的项目，自己重新填写，我的代码如下

https://gitee.com/fakerlove/machine-learning/tree/master/code

代码原链接

8. 吴恩达机器学习课程-作业8-异常检测和推荐系统

在本练习中，您将实现异常检测算法和应用它来检测网络上出现故障的服务器。

在第二部分，你会看到使用协同过滤为电影建立一个推荐系统。

之前在开始编程练习时，我们强烈建议观看完成相关主题的复习问题。

要开始练习，您需要下载启动器代码并将其内容解压缩到您希望完成的目录锻炼。

如果需要，使用Octave/MATLAB中的cd命令更改为这个目录，然后开始这个练习。

你也可以在课程网站的“En环境设置说明”中找到安装Octave/MATLAB的说明。

8.1 异常检测

Anomaly detection

这是也是一个非监督学习算法

• 异常检测做什么？
  从一组数据中找到那些“异常”的数据，基于高斯分布（正太分布）。生活中的很多事情都是符合高斯分布的，对于数据也是如此。我们通过参数估计，估计出数据符合的高斯分布参数，当其中的数据分布在高斯分布中概率很小的地方，就认为这是异常数据。

• 具体怎么做？
  选择可以描述异常状态的特征作为输入$x^{(1)},x^{(2)},\dots ,x^{(m)}$

  根据以往的数据估计高斯分布的参数(对每一个特征)
  $$\begin{gathered} {\mu }_j=\frac{1}{m}\sum _{i=0}^m{x}_j^{(i)} \\ {\sigma }_j^2=\frac{1}{m}\sum _{i=0}^m(x_j^{(i)}-{\mu }_j{)}^2 \end{gathered}$$

• 对于一个新的数据，预测其发生概率

  $P(x)={\prod }_{j=1}^{n}P(x_j;{\mu }_j;{\sigma }_j^2)={\prod }_{j=1}^n\frac{1}{\sqrt{2\pi }{\sigma }_j}{e}^{-\frac{(x_j-{\mu }_{)}^{2}j}{2{\sigma }_j^2}}$

当概率小于一定阈值后认定为异常。

这个算法有什么缺点？
可以看到，之前的模型中对每个特征都是独立地处理，最后的组合只是简单的相乘。这样就是存在一些问题，特征之间的关联没有捕捉到。
升级的方式就是多元高斯分布，将不再单独考虑特征，而是将特征一起考虑，自动捕捉之间的关联。
参数的估计变为，其中的sigma为协方差矩阵
$$\begin{gathered} \mu =\frac{1}{m}\sum _{i=1}^m{x}^{(i)} \\ \Sigma =\frac{1}{m}\sum _{i=1}^m(x^{(i)}-\mu )(x^{(i)}-\mu {)}^T \end{gathered}$$
预测变为
$$P(x;\mu ;\Sigma )=\frac{1}{(2\pi {)}^{\frac{n}{2}}|\Sigma {|}^{\frac{1}{2}}}{e}^{-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )}$$

• 这个模型有个前提就是m>n，而且协方差矩阵是非奇异矩阵。另外这个计算也是复杂的。
• 怎么评估算法的效果？
  使用标签化的数据，计算F1score
• 怎么感觉异常检测可以用监督学习做呢？
  总结一下异常检测和监督学习的适合场景
  • 异常检测
    （1）异常数据很少，y=1的数据很少
    （2）正常数据很多，y=0的数据很多
    （3）异常的类型太多
    （4）未来异常的类型是未知的
    典型应用：欺骗检测，监测机器
  • 监督学习
    （1）y=0和y=1的数据都很多
    （2）异常的例子够多，且未来的异常与以往相同
    典型应用：垃圾邮件分类，天气预测

8.1.1 题目介绍

在本练习中，您将实现一个异常检测算法来进行检测服务器计算机的异常行为。

这些特性测量每个服务器的吞吐量(mb/s)和响应延迟(ms)。

当你的服务器你收集了307个关于它们行为的例子，因此有一个未标记的数据集 { x ( 1 ) ， … x ( m ) } \{x^{(1)}，…x^{(m)}\} {x(1)，…x(m)}。

你怀疑这些例子中的绝大多数是“正常”(非反常)的例子服务器运行正常，但也可能有一些例子该数据集中异常操作的服务器。

您将使用一个高斯模型来检测异常的例子数据集。

您将首先从允许可视化的2D数据集开始算法在做什么。

在那个数据集上，你将适合一个高斯分布，然后找到概率非常低的值，因此可以被认为是异常。

之后，您将应用异常检测算法到一个更大的多维度数据集。你将使用ex8.m这部分的练习。

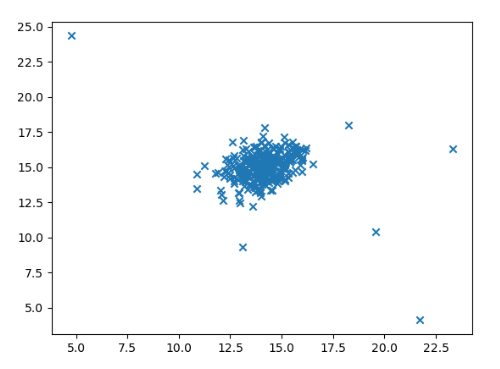
8.1.2 可视化数据

    data = sio.loadmat("data\\ex8data1.mat")
    X = np.array(data['X'])  # (307,2)
    plt.scatter(X[..., 0], X[..., 1], marker='x', label='point')
    plt.show()

8.1.3 代码

1) 高斯分布

假设我们已经知道了高斯模型的参数,计算概率

def gaussian_distribution(X, mu, sigma2):
    """
    根据高斯模型参数，计算概率
    :param X: ndarray,数据
    :param mu: ndarray,均值
    :param sigma2: ndarray,方差
    :return: ndarray,概率
    """
    p = (1 / np.sqrt(2 * np.pi * sigma2)) * np.exp(-(X - mu) ** 2 / (2 * sigma2))
    return np.prod(p, axis=1)  # 横向累乘

2) 估计高斯参数

根据数据估计出模型的参数

def estimate_parameters_for_gaussian_distribution(X):
    """
    估计数据估计参数
    :param X: ndarray,数据
    :return: (ndarray,ndarray),均值和方差
    """
    mu = np.mean(X, axis=0)  # 计算方向因该是沿着0，遍历每组数据
    sigma2 = np.var(X, axis=0)  # N-ddof为除数,ddof默认为0
    return mu, sigma2

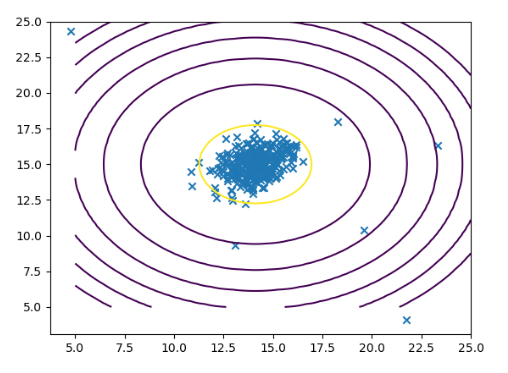
根据估计出的参数，画出高斯分布的等高线

def visualize_contours(mu, sigma2):
    """
    画出高斯分布的等高线
    :param mu: ndarray,均值
    :param sigma2: ndarray,方差
    :return: None
    """
    x = np.linspace(5, 25, 100)
    y = np.linspace(5, 25, 100)
    xx, yy = np.meshgrid(x, y)
    X = np.concatenate((xx.reshape(-1, 1), yy.reshape(-1, 1)), axis=1)
    z = gaussian_distribution(X, mu, sigma2).reshape(xx.shape)
    cont_levels = [10 ** h for h in range(-20, 0, 3)]  # 当z为当前列表的值时才绘出等高线
    plt.contour(xx, yy, z, cont_levels)

使用

    mu, sigma2 = estimate_parameters_for_gaussian_distribution(X)
    p = gaussian_distribution(X, mu, sigma2)
    visualize_contours(mu, sigma2)

3) 选择阈值

要判断出是否为异常，需要一个阈值。可以通过取不同的阈值，计算标签数据的F1score等量化的评价的标准，选取最好的阈值。
首先需要对模型计算出的结果，进行误差分析，计算F1-score。这里需要注意，F1-score，precision和recall的计算，需要判断分母为0的情况。

def error_analysis(yp, yt):
    """
    计算误差分析值F1-score
    :param yp: ndarray,预测值
    :param yt: ndarray,实际值
    :return: float,F1-score
    """
    tp, fp, fn, tn = 0, 0, 0, 0
    for i in range(len(yp)):
        if yp[i] == yt[i]:
            if yp[i] == 1:
                tp += 1
            else:
                tn += 1
        else:
            if yp[i] == 1:
                fp += 1
            else:
                fn += 1
    precision = tp / (tp + fp) if tp + fp else 0  # 防止除以0
    recall = tp / (tp + fn) if tp + fn else 0
    f1 = 2 * precision * recall / (precision + recall) if precision + recall else 0
    return f1

封装阈值选择函数，阈值从预测值的最小到最大的范围中遍历，计算F1-score选择出最好的阈值选择

def select_threshold(yval, pval):
    """
    根据预测值和真实值确定最好的阈值
    :param yval: ndarray,真实值（这里是0或1）
    :param pval: ndarray,预测值（这里是[0,1]的概率）
    :return: (float,float),阈值和F1-score
    """
    epsilons = np.linspace(min(pval), max(pval), 1000)
    l = np.zeros((1, 2))
    for e in epsilons:
        ypre = (pval < e).astype(float)
        f1 = error_analysis(ypre, yval)
        l = np.concatenate((l, np.array([[e, f1]])), axis=0)
    index = np.argmax(l[..., 1])
    return l[index, 0], l[index, 1]

测试

    Xval = data['Xval']  # (307,2)
    yval = data['yval']  # (307,1)
    e, f1 = select_threshold(yval.ravel(), gaussian_distribution(Xval, mu, sigma2))
    print('best choice of epsilon is ', e, ',the F1 score is ', f1)
    # best choice of epsilon is  8.999852631901393e-05 ,the F1 score is  0.8750000000000001

利用选择出来的阈值完善模型，对异常进行预测。

def detection(X, e, mu, sigma2):
    """
    根据高斯模型检测出异常数据
    :param X: ndarray,需要检查的数据
    :param e: float,阈值
    :param mu: ndarray,均值
    :param sigma2: ndarray,方差
    :return: ndarray,异常数据
    """
    p = gaussian_distribution(X, mu, sigma2)
    anomaly_points = np.array([X[i] for i in range(len(p)) if p[i] < e])
    return anomaly_points

我们将异常的数据点圈出来

def visualize_dataset(X):
    plt.scatter(X[..., 0], X[..., 1], marker='x', label='point')
    
def circle_anomaly_points(X):
    plt.scatter(X[..., 0], X[..., 1], s=80, facecolors='none', edgecolors='r', label='anomaly point')

使用

    anomaly_points = detection(X, e, mu, sigma2)
    circle_anomaly_points(anomaly_points)
    plt.title('anomaly detection')
    plt.legend()
    plt.show()

4) 高维数据集

异常检测的方法都写好了，对于高维的数据，也是一样的操作就行

    data2 = sio.loadmat("data\\ex8data2.mat")
    X = data2['X']
    Xval = data2['Xval']
    yval = data2['yval']
    mu, sigma2 = estimate_parameters_for_gaussian_distribution(X)
    e, f1 = select_threshold(yval.ravel(), gaussian_distribution(Xval, mu, sigma2))
    anomaly_points = detection(X, e, mu, sigma2)
    print('\n\nfor this high dimensional dataset \nbest choice of epsilon is ', e, ',the F1 score is ', f1)
    print('the number of anomaly points is', anomaly_points.shape[0])
# for this high dimensional dataset 
# best choice of epsilon is  1.3786074982000235e-18 ,the F1 score is  0.6153846153846154
# the number of anomaly points is 117

8.2 推荐系统

8.2.1 题目介绍

拿电影网站来说，通常我们都会给自己看过的电影评分，作为网站运营者要进行其他电影的推荐，那么就需要根据你之前的评分。
假设我们对每个电影给出一个向量x代表一系列特征，那么根据用户对部分电影的评分，我们可以使用线性回归的方式求出一个向量theta这个向量代表用户的一系列特征，那么我们就可以通过计算theta^T·x得到对于用户未评分电影的预测评分，就可以通过这个进行推荐。
从令一个角度看，假设我们对每个用户给出一个向量theta，与上面相同的方法，也可以求出电影的特征向量x，同样进行电影评分预测。
但是不管是用户特征还是电影特征都难以手动确定，那怎么实现推荐系统呢？
协同过滤算法

现实情况是我们都不知道用户特征和电影特征，只知道用户对哪些电影评分，评分的分数。协同过滤算法的思路是我们直接一起训练用户特征和电影特征，首先随机初始化用户特征和电影特征，在每一次梯度下降过程中，先后更新用户特征和电影特征，最后就能得到用户特征和电影特征并进行预测。
为什么可以先后跟新用户特征和电影特征呢？因为他们的优化目标函数是相同的。
$$\begin{gathered} J(x^{(1)},\dots ,x^{(n_m)};{\theta }^{(1)},\dots ,{\theta }^{(n_u)}) \\ =\frac{1}{2}\sum _{(i,j):r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i,j)}{)}^2+\frac{\lambda }{2}\sum _{i=1}^{n_m}\sum _{k=1}^n(x_k^{(i)}{)}^2+\frac{\lambda }{2}\sum _{j=1}^{n_u}\sum _{k=1}^n({\theta }_k^{(j)}{)}^2 \end{gathered}$$

只需要保证用户特征和电影特征的特征数量是相同的即可
具体的算法流程是：
1.随机初始化用户特征theta和电影特征x，这里需要保证两个维度一样
2.使用梯度下降或其他优化算法更新两个特征参数
$$\begin{gathered} x_k^{(i)}=x_k^{(i)}-\alpha (\sum _{(i,j):r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i,j)}){\theta }_k^{(j)}+\lambda x_k^{(i)}) \\ {\theta }_k^{(j)}={\theta }_k^{(j)}-\alpha (\sum _{(i,j):r(i,j)=1}(({\theta }^{(j)}{)}^T{x}^{(i)}-y^{(i,j)})x_k^{(i)}+\lambda {\theta }_k^{(j)}) \end{gathered}$$

3.用着两个特征预测评分，进行排序推荐
$$predict={\theta }^{T}x$$

8.2.2 代码

1) 协同过滤代价函数

实现目标函数，参数应该是一维向量，需要将用户特征和电影特征一维序列化，在计算损失值内部还原为原来的形式

def serialize(X, theta):
    """
    参数一维向量化
    :param X: ndarray,电影特征
    :param theta: ndarray,用户特征
    :return: ndarray,一维化向量
    """
    return np.concatenate((X.flatten(), theta.flatten()), axis=0)


def deserialize(params, nm, nu, nf):
    """
    将一维化参数向量还原
    :param params: ndarray,一维化的用户特征和电影特征
    :param nm: int,电影数量
    :param nu: int,用户数量
    :param nf: int,特征数量
    :return: (ndarray,ndarray) 电影特征,用户特征
    """
    X = params[:nm * nf].reshape(nm, nf)
    theta = params[nm * nf:].reshape(nu, nf)
    return X, theta

然后我们再来实现损失值计算，这里直接将正则化项加入。这里与线性回归不同的地方就是不用添加$x_0$和${\theta }_0$​，正则化项里面就不需要去掉0项

def collaborative_filtering_cost(params, Y, R, nm, nu, nf, l=0.0):
    """
    协同过滤算法目标函数
    :param params: ndarray,一维化的用户特征和电影特征
    :param Y: ndarray,表明用户的评分
    :param R: ndarray,表明哪些用户评价了哪些电影
    :param nm: int,电影数量
    :param nu: int,用户数量
    :param nf: int,特征数量
    :param l: float,惩罚参数
    :return: float,损失值
    """
    X, theta = deserialize(params, nm, nu, nf)
    part1 = np.sum(((X.dot(theta.T) - Y) ** 2) * R) / 2
    part2 = l * np.sum(theta ** 2) / 2
    part3 = l * np.sum(X ** 2) / 2
    return part1 + part2 + part3

测试不带正则化项时，直接将参数赋为 0

    data1 = sio.loadmat("data\\ex8_movies.mat")
    Y = data1["Y"]  # (1682,943)
    R = data1["R"]  # (1682,943)
    data2 = sio.loadmat("data\\ex8_movieParams.mat")
    X = data2["X"]  # (1682,10)
    theta = data2["Theta"]  # (943,10)
    nu = data2["num_users"][0][0]  # (1,1) 943
    nm = data2["num_movies"][0][0]  # (1,1) 1682
    nf = data2["num_features"][0][0]  # (1,1) 10
    # 题目中计算数据不是全部数据，取nm=5,nu=4,nf=3,值为22.224603725685675
    nu = 4
    nm = 5
    nf = 3
    X = X[:nm, :nf]
    theta = theta[:nu, :nf]
    Y = Y[:nm, :nu]
    R = R[:nm, :nu]
    print(collaborative_filtering_cost(serialize(X, theta), Y, R, nm, nu, nf))
    # 22.224603725685675

2) 协同过滤梯度

实现协同过滤梯度下降，这里也先实现正则部分

def collaborative_filtering_gradient(params, Y, R, nm, nu, nf, l=0.0):
    """
    协同过滤梯度下降
    :param params: ndarray,一维化的用户特征和电影特征
    :param Y: ndarray,表明用户的评分
    :param R: ndarray,表明哪些用户评价了哪些电影
    :param nm: int,电影数量
    :param nu: int,用户数量
    :param nf: int,特征数量
    :param l: float,惩罚参数
    :return: ndarray,跟新后的一维化的用户特征和电影特征
    """
    X, theta = deserialize(params, nm, nu, nf)
    g_X = ((X.dot(theta.T) - Y) * R).dot(theta) + l * X
    g_theta = ((X.dot(theta.T) - Y) * R).T.dot(X) + l * theta
    return serialize(g_X, g_theta)

3) 正规化的损失函数

上面已经完成

4) 检查梯度

测试需要用到梯度下降检测，就是求一个近视的导数。不知道为什么，梯度下降检测运行得太慢，没有跑出结果。

def check_gradient(params, Y, R, nm, nu, nf):
    # X, theta = deserialize(params, nm, nu, nf)
    e = 0.0001
    m = len(params)
    g_params = np.zeros((m,))
    for i in range(m):
        temp = np.zeros((m,))
        temp[i] = e
        g_params[i] = (collaborative_filtering_cost(params + temp, Y, R, nm, nu, nf) -
                       collaborative_filtering_cost(params - temp, Y, R, nm, nu, nf)) / (2 * e)
    return g_params

5) 学习电影推荐

这里训练模型，首先添加自定义数据

    # 先添加一组自定义的用户数据
    my_ratings = np.zeros((1682, 1))
    my_ratings[0] = 4
    my_ratings[97] = 2
    my_ratings[6] = 3
    my_ratings[11] = 5
    my_ratings[53] = 4
    my_ratings[63] = 5
    my_ratings[65] = 3
    my_ratings[68] = 5
    my_ratings[182] = 4
    my_ratings[225] = 5
    my_ratings[354] = 5

    Y = np.concatenate((Y, my_ratings), axis=1)
    R = np.concatenate((R, my_ratings > 0), axis=1)
    nu += 1

利用scipy.optimize.minimize()的高级优化方法去做

    params = serialize(np.random.random((nm, nf)), np.random.random((nu, nf)))
    res = opt.minimize(fun=collaborative_filtering_cost, x0=params, args=(Y, R, nm, nu, nf, 10),
                       method='TNC',
                       jac=collaborative_filtering_gradient)

利用优化后的参数进行预测

    trained_X, trained_theta = deserialize(res.x, nm, nu, nf)
    predict = trained_X.dot(trained_theta.T)
    my_predict = predict[..., -1]

选出十个最高的评分，显示推荐结果。我们还要读入电影名。

    # 读入电影标签
    f = open("data\\movie_ids.txt", "r")
    movies = []
    for line in f.readlines():
        movies.append(line.split(' ', 1)[-1][:-1])

测试

	# 先打印构造的用户数据
    for i in range(len(my_ratings)):
        if my_ratings[i] > 0:
            print(my_ratings[i], movies[i])
    # 从预测结果中选10个最优推荐
    # 由于训练初始化参数的不同会导致最后的结果不同
    print("Top recommendations for you:")
    for i in range(10):
        index = int(np.argmax(my_predict))
        print("Predicting rating ", my_predict[index], " for movie ", movies[index])
        my_predict[index] = -1

结果

========程序开始============
     fun: 71897.36471818546
     jac: array([ 3.60276253e-05,  3.58357454e-05,  1.25200625e-05, ...,
       -7.07931584e-08,  1.67499863e-06,  1.87570976e-07])
 message: 'Converged (|f_n-f_(n-1)| ~= 0)'
    nfev: 1068
     nit: 40
  status: 1
 success: True
       x: array([0.83047824, 0.26308883, 1.03427066, ..., 0.37918117, 0.589567  ,
       0.80432564])
[4.] Toy Story (1995)
[3.] Twelve Monkeys (1995)
[5.] Usual Suspects, The (1995)
[4.] Outbreak (1995)
[5.] Shawshank Redemption, The (1994)
[3.] While You Were Sleeping (1995)
[5.] Forrest Gump (1994)
[2.] Silence of the Lambs, The (1991)
[4.] Alien (1979)
[5.] Die Hard 2 (1990)
[5.] Sphere (1998)
Top recommendations for you:
Predicting rating  4.291403110734195  for movie  Titanic (1997)
Predicting rating  4.11995465780804  for movie  Star Wars (1977)
Predicting rating  3.979219524675847  for movie  Raiders of the Lost Ark (1981)
Predicting rating  3.9099981655253253  for movie  Good Will Hunting (1997)
Predicting rating  3.885805275675247  for movie  Shawshank Redemption, The (1994)
Predicting rating  3.872955442386821  for movie  Return of the Jedi (1983)
Predicting rating  3.871294096581197  for movie  Braveheart (1995)
Predicting rating  3.86300516603891  for movie  Empire Strikes Back, The (1980)
Predicting rating  3.757933627189945  for movie  Terminator 2: Judgment Day (1991)
Predicting rating  3.757686577873416  for movie  As Good As It Gets (1997)
当前训练对岳原始数据集的均方误差 0.6400023145811953
========程序结束============
该循环程序运行时间： 87.01877641677856