K-means的改进

最新推荐文章于 2025-02-13 17:47:46 发布

宝哥大数据

最新推荐文章于 2025-02-13 17:47:46 发布

阅读量9.8k

点赞数 12

分类专栏： # 机器学习

本文链接：https://blog.csdn.net/wuxintdrh/article/details/105425314

版权

机器学习专栏收录该内容

60 篇文章

订阅专栏

前言

k-means算法是数据挖掘十大经典算法之一，已出现了很多的改进或改良算法。例如

1、对k的选择可以先用一些算法，分析数据的分布，如重心和密度等，然后选择合适的k。
2、有人提出了二分k均值（bisecting k-means）算法，它对初始的k个质心的选择就不太敏感。
3、基于图划分的谱聚类算法，能够很好地解决非凸数据的聚类。

一、Canopy算法配合初始聚类

1.1、算法原理

选择质心，T1圆内的点归为本簇，T1到T2范围内的点属于可疑点(黑色的点)， T2外的点为簇外点（绿色的点）
从簇外点中选择质心，然后根据T1,T2划分
- T1范围内的可疑点，划到本簇，
- 直到所有的簇外点划分完成
  
  划分完成，对于较小的簇将其去掉，此时的K值可以作为K-means的初始K值

1.2、Canopy的优缺点

1.2.1、优点

1、 Kmeans对噪声抗干扰较弱，通过Canopy 对比，将较小的NumPoint的Cluster直接去掉有利于抗干扰。
2、Canopy选择出来的每个Canopy的centerPoint作为K会更精确。
3、只是针对每个Canopy的内做Kmeans聚类，减少相似计算的数量。

1.2.2、缺点（问题）

这和需要设置初始条件的算法都有的通病，就是初始条件的选取

算法中 T1、T2的确定问题

二、K-means++

$\frac{D(x)^2}{\sum_{x \in X}D(x)^2}$

参考：https://www.cnblogs.com/wang2825/articles/8696830.html

其实这个算法也只是对初始点的选择有改进而已，其他步骤都一样。初始质心选取的基本思路就是，初始的聚类中心之间的相互距离要尽可能的远。

算法描述如下：

步骤一：随机选取一个样本作为第一个聚类中心 c1；
步骤二：
- 计算每个样本与当前已有类聚中心最短距离（即与最近一个聚类中心的距离），用 D(x)表示；这个值越大，表示被选取作为聚类中心的概率较大；
- 最后，用轮盘法选出下一个聚类中心；
步骤三：重复步骤二，知道选出 k 个聚类中心。
选出初始点后，就继续使用标准的 k-means 算法了

三、二分K-means

3.1、算法思路

所有点作为一个簇
将该簇一分为二
选择能最大限度降低聚类代价函数（也就是误差平方和SSE）的簇划分为两个簇。
以此进行下去，直到簇的数目等于用户给定的数目k为止。

在这里插入图片描述

3.2、算法实现

#二分kmeans        
def biKmeans(dataSet, k, distMeas=distEclud):
    m = shape(dataSet)[0]
    clusterAssment = mat(zeros((m,2)))
    #所有样本看成一个簇，求均值
    centroid0 = mean(dataSet, axis=0).tolist()[0]#axis=0按列，matrix->list
    centList =[centroid0] #create a list with one centroid
    for j in range(m): #计算初始总误差SSE
        clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
    #当簇数<k时
    while (len(centList) < k):
        lowestSSE = inf  #初始化SSE
        #对每个簇
        for i in range(len(centList)):
            #获取当前簇cluster=i内的数据
            ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:]
            
            #对cluster=i的簇进行kmeans划分，k=2
            centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas)
            
            #cluster=i的簇被划分为两个子簇后的SSE
            sseSplit = sum(splitClustAss[:,1])
            
            #除了cluster=i的簇，其他簇的SSE
            sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1])
            print("sseSplit, and notSplit: ",sseSplit,sseNotSplit)
            
            #找最佳的划分簇，使得划分后 总SSE=sseSplit + sseNotSplit最小
            if (sseSplit + sseNotSplit) < lowestSSE: 
                bestCentToSplit = i    
                bestNewCents = centroidMat #被划分簇的两个新中心
                bestClustAss = splitClustAss.copy() #被划分簇的聚类结果0,1 ，及簇内SSE
                lowestSSE = sseSplit + sseNotSplit
                
        #将最佳被划分簇的聚类结果为1的类别，更换类别为len(centList)
        bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList)  
        
        #将最佳被划分簇的聚类结果为0的类别，更换类别为bestCentToSplit
        bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit
        print('the bestCentToSplit is: ',bestCentToSplit)
        print('the len of bestClustAss is: ', len(bestClustAss))
        
        #将被划分簇的一个中心，替换为划分后的两个中心
        centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] 
        centList.append(bestNewCents[1,:].tolist()[0])
        
        #更新整体的聚类效果clusterAssment(类别，SSE)
        clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss
        #kMeans.datashow(dataSet,len(centList),mat(centlist),clusterAssment)   
    return mat(centList), clusterAssment

四、Kernel k-means

线性可分与线性不可分，通过核函数将数据提升到高维，是的在低维线性不可分的数据，变成高维的线性可分。

4.1、通过映射关系，将数据映射到高维空间，然后在高维可以线性可用

注意：核函数是用来计算映射后的内积，

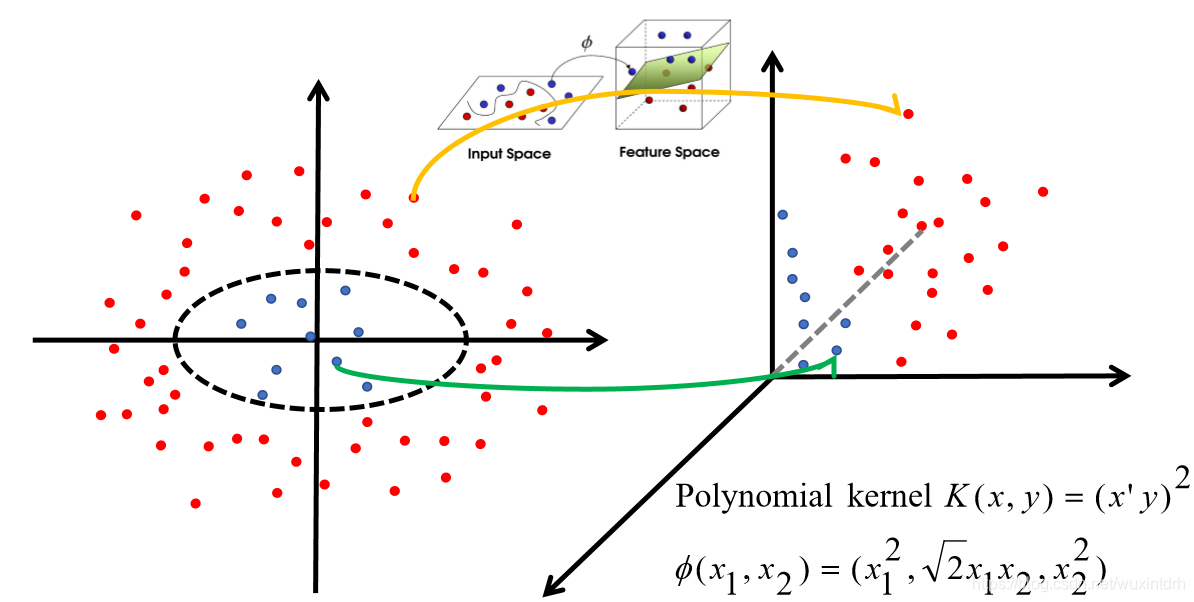
在这里插入图片描述
将每个样本进行一个投射到高维空间的处理，然后再将处理后的数据使用普通的k-means算法思想进行聚类。

五、 k-medoids（k-中心聚类算法）

5.1、原理

K-medoids和K-means是有区别的，不一样的地方在于中心点的选取：

K-means中，将中心点取为当前cluster中所有数据点的平均值，对异常点很敏感!
K-medoids法选取的中心点为当前cluster中存在的一点，准则函数是当前cluster中所有其他点到该中心点的距离之和最小，这就在一定程度上削弱了异常值的影响，但缺点是计算较为复杂，耗费的计算机时间比K-means多。

K-medoids使用绝对差值和（Sum of Absolute Differences，SAD）的度量来衡量聚类结果的优劣，在n维空间中，计算SAD的公式如下所示：
在这里插入图片描述

5.1、算法流程

( 1 )总体n个样本点中任意选取k个点作为medoids
( 2 )按照与medoids最近的原则，将剩余的n-k个点分配到当前最佳的medoids代表的类中
( 3 )对于第i个类中除对应medoids点外的所有其他点，按顺序计算当其为新的medoids时，代价函数的值，遍历所有可能，选取代价函数最小时对应的点作为新的medoids
( 4 )重复2-3的过程，直到所有的medoids点不再发生变化或已达到设定的最大迭代次数
( 5 )产出最终确定的k个类

5.2、K-Menas与K-Medoids的对比

在这里插入图片描述

六、ISODATA(迭代自组织数据分析算法)

在K-均值算法的基础上，对分类过程增加了“合并”和“分裂”两个操作，并通过设定参数来控制这两个操作的一种聚类算法。

“合并”：当聚类结果某一类中样本数太少，或两个类间的距离太近
“分裂”:当聚类结果中某一类的类内方差太大，将该类进行分裂

七、Mini Batch K-Means（适合大数据的聚类算法）

大数据量是什么量级？通过当样本量大于1万做聚类时，就需要考虑选用Mini Batch K-Means算法。
Mini Batch KMeans使用了Mini Batch（分批处理）的方法对数据点之间的距离进行计算。 Mini Batch 计算过程中不必使用所有的数据样本，而是从不同类别的样本中抽取一部分样本来代表各自类型进行计算。由于计算样本量少，所以会相应的减少运行时间，但另一方面抽样也必然会带来准确度的下降。

小结

在这里插入图片描述