【编译原理】第五章自下而上语法分析

fei_sun

于 2025-05-07 21:32:18 发布

阅读量695

点赞数 15

分类专栏：编译原理文章标签：编译原理

本文链接：https://blog.csdn.net/wuyufei_sun/article/details/147773325

版权

编译原理专栏收录该内容

13 篇文章

订阅专栏

【编译原理】第四章自上而下语法分析-CSDN博客

自下而上分析基本问题

从输入符号串开始，查找当前句柄，并用产生式将它归约成相应的非终结符，最后归约为开始符号

（句柄、归约等概念见【编译原理】一二章-CSDN博客）

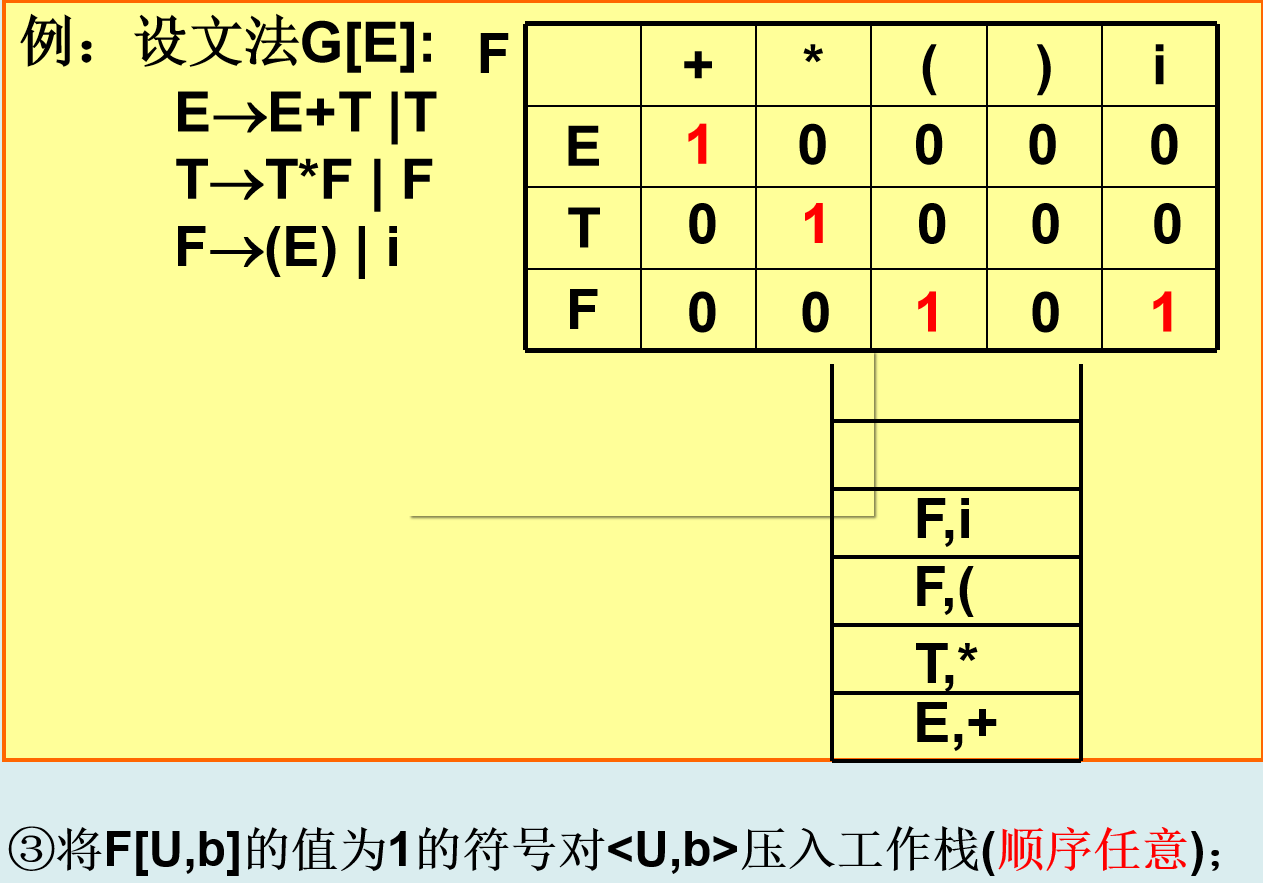
例

自上而下分析法，也称为“移进-归约”法，其一般过程为：

（1）设置一个存放符号的栈称为符号栈，用于记录分析的过程和确定下一步的动作

（2）把输入符号串按扫描顺序逐个移进栈里（符号栈），当栈顶的符号组成的符号串形成一个句柄时（正好是某条产生式的右部），就进行归约。即把该符号串用与它对应的产生式左部的非终结符号代替，仍然置于栈顶

（3）接着检查新栈顶，若形成新的句柄，再进行归约，如没有形成新句柄，则从符号串种移进新的符号。如此重复，直到整个输入符号处理完毕为止

（4）若最终栈底为识别符号，则表明所分析的输入串合法，报告分析成功；否则是不合法的符号串，报告出错信息

注：

(1)对输入符号串的扫描，采用自左向右的顺序；

(2)分析过程是自下而上进行的(对语法树来说从末端结点开始，最后归约到根结点)；

(3)每次归约是对最左简单短语(句柄)进行的；

(4)算法的关键是确定最左简单短语。

算符优先分析法

算符优先分析法是自下而上分析方法中的一种，虽然它不是规范（最左）归约，但它具有分析速度快，特别适合表达式分析的特点，因而得到普遍应用。

A+B*C/D-E/F*G

算符文法：

任意产生式的右部不含有两个相继的非终结符

注：相继和相邻，相邻一定相继

FIRSTVT、LASTVT

假设有个产生式的一个候选形为

........aP........

对于任何b $\in$ FIRSTVT(P)，有a $< \cdot$ b

假设有个产生式的一个候选形为

.......Pb.....

对于任何a $\in$ LASTVT(P)，有a $\cdot >$ a

aP

Pa

ab

aPb

算符优先文法

设有一个不含空产生式的算符文法（反应各终结符之间优先关系的优先关系矩阵），如果在任意两个终结符号之间，至多只有一种优先关系成立，则称这样的算符文法为算符优先文法 (Operator Precedence Grammar)，即OPG文法。

算符优先分析算法

过程

void Isleft( )
{  Stack s;
   k=1;
   s[k]=’#’;
   do{   把下一个输入符号读进a中；
            if (S[k]∈VT)   j=k;
            else                j=k-1;
            while(S[j]>a)
            {  do{    Q=S[j];
                         if(S[j-1] ∈VT)   j=j-1;
                        else                   j=j-2;
                    }while(S[j]>Q);
              把S[j+1]…S[k]归约为某个N；
              k=j+1;
             S[k]=N;
            }
           if(S[j]<a || S[j]=a)
           {   k=k+1;
               S[k]=a;
            }
          }while(a!=’#’);
}